Простейшей моделью кристалла является правильно построенная кристаллическая решетка, в узлах которой помещаются атомы (или ионы, молекулы), принимаемые за материальные точки. Атом совершает тепловые колебания около положения равновесия. Если колебания малы, то они будут гармоническими. Энергия каждого атома слагается из потенциальной Wп и кинетической Wк. Известно [ cм. конспект лекций Физика, ч. I, лекции 11, 12 формулы (7), (8)], что в случае гармонических колебаний
Wп=(1/2) kA 2 cos 2 (wt+q)=(1/4) kA 2 [1+cos2(wt+q)], (1)
Wк=(1/2) kA 2 sin 2 (wt+q)=(1/4) kA 2 [1-сos2(wt+q)].
В лекции 4 показано, что на каждую степень свободы приходиться в среднем кинетическая энергия (1/2)kT. Атом имеет 3 степени свободы, поэтому K>=n>=(3/2)kT. Таким образом средняя энергия атома =K>+n>=3kT. Умножив эту величину на постоянную Авогадро NA (число атомов в моле вещества), найдем внутреннюю энергию моля твердого тела
где R=kNA=8.31 Дж/мольК — универсальная газовая постоянная. Отсюда молярная теплоемкость твердого тела
Теплоемкость. Теплоемкость газа. Молярная теплоемкость
C=dU/dT=3R»25 Дж/(моль×К). (3)
Этотзакон был эмпирически (опытным путем) установлен в 1919 г. Дюлонгом и Пти. Он утверждает:
Молярная теплоемкость для всех простых твердых тел равна 3R, т.е.

C=3R. (4)

Для многих веществ этот закон хорошо выполняется, хотя некоторые вещества (алмаз С, Ве, В) имеют значительные отклонения от вычисленных теплоёмкостей. Опыт также показал, что С зависит от температуры и вблизи нуля кельвин для всех веществ С~ . На рис. 1 представлена характерная экспериментально полученная зависимость С от Т. Расхождение опытных и теоретических значений теплоёмкостей объяснили, исходя из квантовой теории теплоёмкости, Эйнштейн и Дебай.
8.2 Понятие о квантовой теории теплоёмкости Эйнштейна и Дебая
Эйнштейн рассматривал кристалл как систему из N атомов, каждый из которых является квантовым гармоническим осциллятором (осциллятор — это физическая система, совершающая колебания). Колебания всех атомов происходят независимо друг от друга с одинаковой частотой n. Средняя энергия áЕñ, приходящая на одну степень свободы атома — гармонического квантового осциллятора:

. (5)

Внутренняя энергия моля твёрдого тела U = 3NAáEñ = ,
отсюда молярная теплоёмкость твёрдого тела

. (6)
Этот результат качественно описывает зависимость С от Т, однако в области низких температур возникают расхождения с экспериментально полученными зависимостями С от Т.
Дебай развил теорию Эйнштейна. Он учёл, что:
Количество теплоты. Способы изменения внутренней энергии. Теплоемкость. 10 класс.
1) колебания атомов в кристаллической решётке не являются независимыми и
2) основной вклад в энергию тепловых колебаний кристалла при низких температурах вносят колебания низких частот.
Таким образом, тепловое возбуждение твёрдого тела Дебай описал в виде упругих (звуковых) волн, распространяющихся в кристалле. Упругие волны в кристалле имеют квантовые свойства, проявляющиеся в том, что существует наименьшая порция — квант энергии волны с данной частотой n. Упругим волнам в кристалле сопоставляют фононы, обладающие энергией Е = hn.
Фонон есть квант энергии звуковой (упругой) волны. Фононы являются квазичастицами, ведущими себя подобно микрочастицам. Заметим, что квазичастицы, в частности, фононы, не могут возникать и распространяться в вакууме, они существуют только в среде. Таким образом, квантование упругих волн привело к представлениям о фононах подобно тому, как ранее квантование электромагнитного излучения привело к представлению о фотонах.

Как указывалось в предыдущей лекции, фононы относятся к классу бозонов. Система бозонов описывается распределением Бозе-Эйнштейна (7.5). Для фононов m = 0 и ánñ = , поэтому эта функция входила в формулы (5) и (6) данной лекции, с учётом того, что Е = hn.
Обозначим через dn число фононов с частотой в интервале от n до n+dn, тогда внутренняя энергия кристалла (вывод опускается)

, (7)

где nмакс = — максимальная частота фононов, N — число атомов в кристалле с объёмом V, v — скорость звука в кристалле, h, k — постоянные Планка и Больцмана.
При вычислении U вводится характеристическая температура Дебая ТD = hnмакс/k и рассматриваются 2 предельных случая:
1.Высокие температуры Т>>TD (или kT>>hnмакс). При этом  и
и  . Для одного моля N = NA и молярная
. Для одного моля N = NA и молярная
теплоёмкость С = dU/dT = 3NAk = 3R, т. е. соответствует закону Дюлонга и Пти.
2.Низкие температуры TD. В этом случае при вычислении интеграла вводится новая переменная х = hn/(kT) и верхний предел заменяется на ¥:

. (8)

При выводе этой формулы было учтено, что интеграл равен . Молярная теплоёмкость

С = dU/dT = , (9)

т. е. пропорциональна , что подтверждается на опыте. Таким образом, квантовая теория теплоёмкости Эйнштейна и Дебая объяснила теплоёмкость твёрдых тел.
8.3. Теплоёмкость электронного газа в металлах
В металлах теплоёмкость складывается из теплоёмкости ионной решётки (см. параграф 8.2.) и теплоёмкости свободных электронов — электронного газа., т. е. С = Cреш + Сэл. Если бы электронный газ был невырожденный (классический), то каждый электрон обладал бы средней кинетической энергией (3/2)kT и средняя энергия электронного газа в одном моле металла была бы равна (3/2)kT×NA = (3/2)RT. Полная внутренняя энергия моля металла в этом случае была бы U = 3RT + (3/2)RT = (9/2)RT, а молярная теплоёмкость металла С = dU/dT = (9/2)R, т. е. в полтора раза больше теплоёмкости диэлектриков. Однако в действительности теплоёмкость металлов не отличается существенно от теплоёмкости неметаллических кристаллов.
Это противоречие устраняется квантовой теорией.
Средняя энергия теплового движения, равная » kT, составляет при комнатной температуре 1/40 эВ. Такая энергия может возбудить только малую часть электронов, находящихся на самых верхних энергетических уровнях, примыкающих к уровню Ферми. Энергия Ферми EF для хорошо проводящих металлов составляет» 6 эВ [см. (7.4) и комментарий этой формулы]. Действительно, расчёт показывает, что молярная теплоёмкость электронного газа

,
что примерно в 150 раз меньше теплоёмкости твёрдого тела С = 3R при Т = 300 К.

Относительный вклад теплоёмкости электронного газа в теплоёмкость металла будет увеличиваться с уменьшением Т, когда теплоёмкость С, пропорциональная [см. (9)], уменьшается и она будет сравнима или даже будет меньше Сэл, которая пропорциональна Т.
Таким образом, квантовая теория объяснила и теплоёмкость металлов.
Источник: studopedia.org
Классическая теория теплоемкости кристаллов.
Закон Дюлонга — Пти (Закон постоянства теплоёмкости) — эмпирический закон, согласно которому молярная теплоёмкость твёрдых тел при комнатной температуре близка к 3R:
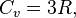
где R — универсальная газовая постоянная.
Закон выводится в предположении, что кристаллическая решетка тела состоит из атомов, каждый из которых совершает гармонические колебания в трех направлениях, определяемыми структурой решетки, причем колебания по различным направлениям абсолютно независимы друг от друга. При этом получается, что каждый атом представляет три осциллятора с энергией E, определяемой следующей формулой:
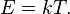

Билет 11.
Колебательные степени свободы и нормальные колебания кристаллической решетки. Максимальная частота нормальных колебаний решетки, оценка для колебаний цепочки упруго связанных атомов (одномерная модель кристалла).
Колебания кристаллической решётки, один из основных видов внутренних движений твёрдого тела, при котором составляющие его частицы (атомы или ионы) колеблются около положений равновесия — узлов кристаллической решётки.
Максимальная частота нормальных колебаний решетки равно числу степеней свободы
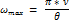
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru
22.3.1. Теплоемкость кристаллов. Модели Дебая и Эйнштейна.
Кристалл представляет собой систему упорядоченно расположенных атомов, обладающих определенными массами; между атомами действуют силы притяжения и отталкивания, уравновешивающие друг друга при определенных равновесных расстояниях между атомами. При отклонении атома из положения равновесия возникает возвращающая сила, противоположная смещению, величина которой зависит от типа атома, его окружения и направления смещения в кристалле. Согласно классической теории колебаний, в такой системе «упруго-связанных масс», состоящей из атомов, имеют место нормальные колебания с собственными частотами , где i = 1, 2, 3. N-4, N-3; причем колебания с частотами , являются независимыми друг от друга; движение атомов может быть представлено как суперпозиция этих нормальных колебаний.
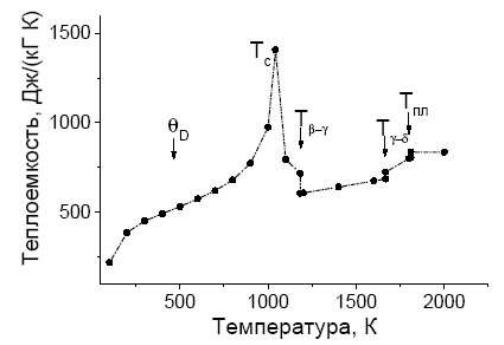
Рис. 22.1. Удельная теплоемкость железа: — температура Дебая; – температура Кюри; и — температуры структурных превращений; — температура плавления
Именно как набор независимых осцилляторов с индивидуальными собственными частотами и рассматривается кристалл, как в классической, так и в квантовой теории тепловых свойств кристаллов и молекул.
Согласно классической теории, при температуре в среднем каждый осциллятор будет обладать энергией ; всего осцилляторов 3N — 3 ~ 3N, следовательно кристалл будет обладать энергией .
Молярная теплоемкость кристалла окажется равной: . Это – известный закон Дюлонга и Пти, утверждающий, что молярная теплоемкость любых кристаллических веществ одна и та же и равна 3R. Он сравнительно хорошо выполняется только при сравнительно высоких температурах порядка 700 — 2000 К. При более низких температурах он не выполняется даже приближенно.
Значительно более точное описание тепловых свойств кристалла дает квантовая теория теплоемкости кристаллов, разработанная Эйнштейном и Дебаем. В ее основе лежит предположение о квантовании энергии колебаний, подобно тому, как квантовалась энергия электромагнитных колебаний в квантовой теории теплового излучения.
Согласно квантовой теории, энергия каждого нормального колебания квантуется по тем же законам, как и энергия одиночного осциллятора. Энергию считают квантом (порцией) энергии колебаний осциллятора, сам же квант принято называть фононом и рассматривать его как частицу, обладающую, в частности, такими свойствами частицы, как энергия и импульс . Взаимная независимость нормальных колебаний позволяет использовать для их описания теорию Бозе-газа, в которой в качестве частиц — бозонов рассматривают фононы. В следующих разделах будет показано, что квантовая теория колебаний кристалла позволяет правильно объяснять многие наблюдаемые на опыте закономерности, в частности, зависимость теплоемкости и теплопроводности от температуры. Эта теория, называемая еще фононной теорией, позволяет объяснять и многие другие явления, связанные с рассеянием излучений и частиц веществом, передачей энергии и заряда. Для многих задач важно знать характеристики фононов, которые можно экспериментально исследовать различными методами.
Как уже отмечалось в начале главы, внутренняя энергия (а затем и теплоемкость) кристалла в принципе может быть вычислена путем определения всех частот нормальных колебаний кристалла и определением энергии всех осцилляторов, используя распределение Бозе-Эйнштейна. Если вторая часть задачи трудностей не вызывает, то ее первая часть чрезвычайно сложна в математическом отношении, она решена в настоящее время только для сравнительно простых молекул. Поэтому были найдены упрощенные способы вычисления спектра собственных частот осцилляторов, некоторые из них рассмотрены в данном разделе.
Модель Эйнштейна. В модели Эйнштейна считают, что атомы колеблются независимо друг от друга и что частоты колебаний всех атомов одинаковы. В таком случае для подсчета внутренней энергии кристалла, содержащего N атомов, достаточно рассмотреть один осциллятор, а затем домножить результат на 3N — число осцилляторов. Пусть каждый осциллятор имеет частоту . Средняя энергия, запасенная в таком осцилляторе, вычисляется с использованием распределения Бозе-Эйнштейна:
где — среднее число квантов энергии, «запасенных» в осцилляторе.
Энергия кристалла, содержащего атомов, тогда вычисляется как , а теплоемкость при постоянном объеме — дифференцированием энергии по температуре:
Модель дает хорошее совпадение с экспериментом для температур выше 50 — 100 К (не слишком близких к абсолютному нулю). График зависимости приведен на рис. 22.2.
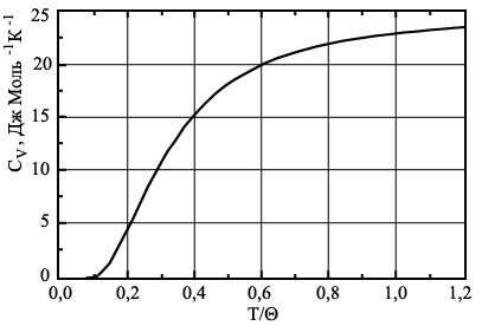
Рис. 22.2. Зависимость теплоемкости от температуры, рассчитанная в рамках модели Эйнштейна для частоты осциллятора, равной
При (случай высоких температур) , что соответствует известному закону Дюлонга и Пти. При (случай низких температур) при , как этого требует третье начало термодинамики. Однако, убывание оказывается более быстрым, чем наблюдают экспериментально . Это связано с некорректностью допущений о независимости колебаний отдельных атомов. Известно, что атомы взаимодействуют друг с другом, в кристалле существуют упругие волны с разной длиной волны, соответствующие коллективным, зависящим друг от друга, колебаниям атомов.
Все же модель Эйнштейна хорошо описывает теплоемкость кристаллов при комнатных и более высоких температурах. Также эта модель идеально подходит для описания теплоемкости отдельных молекул и хорошо подходит для описания вклада оптических фононов (частота которых обычно слабо зависит от волнового вектора) в теплоемкость кристаллов.
Учет коллективных нормальных колебаний атомов значительно уточняет описание теплоемкости при низких температурах. Дело в том, что акустические коллективные колебания имеют более низкие частоты. Энергии тепловых колебаний порядка хватает для их возбуждения. Такие колебания смогут давать вклад в теплоемкость и при низких температурах. Согласно же модели Эйнштейна, все осцилляторы обладают одной сравнительно большой частотой и разностью энергий соседних энергетических уровней , из-за чего переходы с одного уровня осциллятора на другой при низких температурах, если , будут крайне маловероятны, в таком случае и вклад во внутреннюю энергию и в теплоемкость будет очень мал.
Подход к вычислению энергии колебаний кристалла. Как отмечалось выше, вычисление спектра частот нормальных колебаний является слишком сложной задачей. Поэтому при вычислении энергии колебаний атомов в кристалле обычно используют различные упрощения. Чаще всего разрешенные значения волновых векторов фононов вычисляют, рассматривая кубический кристалл с характерным размером . Затем, волновые функции, описывающие упругие колебания кристалла, ищут в комплексном виде:
Далее, накладывают периодические граничные условия на вид функций , описывающих упругие колебания кристалла:
которые выполняются, если:
Тогда волновой вектор может принимать дискретные значения
где — целые числа.
Затем предполагают определенный вид зависимости частоты от волнового вектора . Часто зависимости вычисляют теоретически, а иногда и с учетом полученных экспериментально зависимостей . Область разрешенных значений векторов разбивают на участки, в пределах которых меняется незначительно, чтобы можно было пользоваться формулами, аналогичными используемым в модели Эйнштейна. Затем, как правило, численными методами, суммируют вклады от всех участков в вычисляемую физическую величину, например внутреннюю энергию.
В сферически-симметричных случаях (когда зависит только от модуля ) удобно пользоваться функцией распределения числа нормальных колебаний по частоте , показывающей, сколько нормальных колебаний приходится на интервал частот вблизи :
С помощью можно находить средние значения многих величин, по той же схеме, как это делалось с помощью распределения Максвелла, например:
Функция обязана удовлетворять условию нормировки:
требующему, чтобы общее число нормальных колебаний равнялось .
Рассмотрим применение этого подхода на примере модели Дебая.
Модель Дебая. В рамках модели Дебая считают, что , где — скорость звуковых волн. Такое приближение называется приближением сплошной среды. Ясно, что при таком подходе не удается учесть дисперсию и оптические ветви дисперсионной зависимости фононов.
При этом дополнительно считают, что — взвешенная скорость, то есть имеющая промежуточное значение между скоростями поперечных и продольных волн, как известно сильно отличающихся друг от друга. Зависимость является сферически симметричной, что упрощает расчеты. Число разрешенных векторов , с модулем меньших заданного в таком случае можно найти, разделив объем сферы радиуса в -пространстве на объем, приходящийся на одно разрешенное значение вектора :
Функцию можно найти из соотношения . Величину можно найти аналогичным способом, разделив на величину объема слоя в -пространстве, для которого значения находятся в промежутке . Тогда, с учетом, что , получим выражение для :
Необходимо помнить об условии нормировки. Это условие требует, чтобы общее число осцилляторов равнялось . В рамках модели Дебая просто ограничивают модуль вектора некоторым максимально возможным значением , которое будучи подставленным, даст в левой части — общее число осцилляторов с данным типом поляризации. Выражая и получаем:
Вид функции приведен на рис. 22.3 (кривая 1).
Значения оказываются близкими к , соответствующему границе первой зоны Бриллюэна. Однако следует помнить, что реальная область допустимых значений вектора , совпадающая с первой зоной Бриллюэна, в рамках модели Дебая заменяется на не совпадающую с ней сферу.
Внутренняя энергия, отвечающая всем трем типам поляризации осцилляторов, в рамках теории Дебая вычисляется как интеграл:
Здесь и . Через обозначают температуру Дебая равную:
Следует отметить, что интеграл можно вычислить только численными методами.
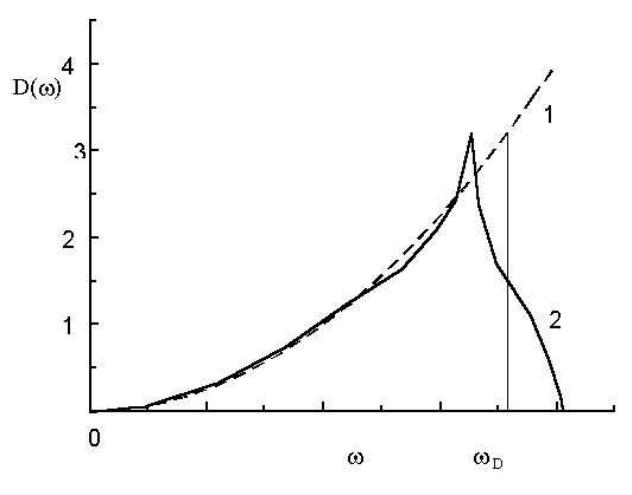
Рис. 22.3. Функция плотности состояний в модели Дебая
Для вычисления теплоемкости следует продифференцировать (22.19) по температуре :
Полученный интеграл можно вычислить только численными методами, график зависимости приведен на рис. 22.4.
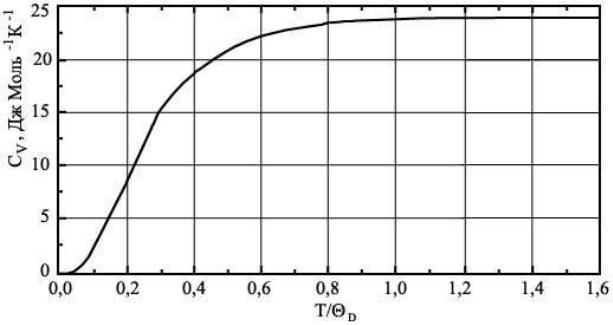
Рис. 22.4. Зависимость теплоемкости , рассчитанная в рамках модели Дебая. По оси абсцисс отложена приведенная температура
При высоких значениях температуры стремится к — классическому значению.
При малых температурах , покажем это. Примем во внимание, что при и . Тогда пределы интегрирования в (22.21) можно считать нулем и бесконечностью. Сам же интеграл в последней формуле окажется равным некоторой константе и зависимость , оказывается очевидной.
Закон при можно получить из следующих достаточно наглядных соображений. При основной вклад в будет обеспечен акустическими колебаниями (а именно их и описывает модель Дебая) с малыми частотами, такими, что . В -пространстве областью таких векторов является сфера, объем которой пропорционален . Каждый фонон в среднем будет иметь энергию порядка . Тогда получается, что «запас» энергии пропорционален числу нормальных колебаний и средней энергии каждого из них, то есть . Теплоемкость можно найти как производную энергии по температуре:
Таким образом модель Дебая сравнительно хорошо описывает зависимость и при низких температурах. Поэтому часто ее используют для приближенного вычисления вклада в теплоемкость от акустических ветвей дисперсионной зависимости фононов, особенно при очень низких температурах. Также ее используют для прогнозирования рассеяния излучений веществом, взаимодействия нейтронов и фотонов с фононами. Для каждого вещества подобрана по сопоставлению с опытными данными о его теплоемкости своя индивидуальная температура Дебая, приводимая в различных справочниках.
Для приближенной аппроксимации оптических ветвей дисперсионной зависимости фононов часто используют модель Эйнштейна или строят модели, похожие на рассмотренную модель Дебая, изменяя в ней зависимость и последующие математические вычисления.
Источник: studfile.net