Четыре проволочных резистора изготовлены из различных материалов и имеют различные размеры серебро

Применение проволок из этих сплавов, улучшили сопротивление проволочных резисторов, уменьшили габариты, повысили температурную стабильность и расширили интервал рабочих температур. Применение защитных покрытий и новых термостойких корпусов, существенно повысило влагостойкость и интервал рабочих температур.
В данной курсовой работе будет рассмотрен проволочный резистор: его параметры, классификация, резистивные материалы, так же будет проведен расчет проволочного резистора.

Введение………………………………………………………………. 4
Общие сведения о резисторах………………………….………. 5
1.1. Классификация резисторов ………………………………………. 6
1.2. Параметры резисторов ……………………………………………. 7
2. Резисторы…………………………………………………………. 10
2.1. Проволочный резистор…………………………………………………. 10
2.2. Постоянный проволочный резистор………………………………. 11
2.3. Переменный проволочный резистор………………………………. 13
3.Резистивные материалы, материалы для проволочных резисторов……………………………………………………………………14
3.1. Резистивные материалы…………………………………………………13

Обзор резистора ВС (УЛИ) и содержание драгметаллов

3.2. Принцип конструирования……………………………………………. 16
3.3. Резистивные материалы на основе благородных материалов………..17
4. Выбор материала резистивного элемента и расчет размеров……. 20
5. Заключение………………………………………………………………..23
6. Список литературы………………………………………………………24

Файлы: 1 файл

1. Резисторы

1. Проволочный резистор

Проволочные резисторы широко применялись в аппаратуре в самом начале становления и развития электроники и электротехники.

Современные проволочные резисторы отличаются высокой стабильностью электрических параметров, малым температурным коэффициентом сопротивления, незначительным уровнем собственных шумов и повышенной точностью.

Все элементы конструкции проволочных резисторов выполняются из термостойких материалов, а проводящий элемент защищен от воздействия внешней среды плотным слоем стеклоэмали, компаунда или герметичным чехлом, что обеспечивает работоспособность резисторов при высоких температурах и повышенной влажности.

Основным элементом проволочных резисторов является тонкая проволока из высокоомного сплава, закрепленная на изолирующем каркасе. Создание миниатюрных проволочных резисторов с высоким значением сопротивления стало возможно благодаря успехам микрометаллургии.

В технологии производства проволочных резисторов применяются сплавы с высоким удельным сопротивлением, достаточной механической прочностью, гибкостью и термостойкостью. Температурный коэффициент сопротивления сплавов должен быть низким, чтобы изменения сопротивления резистора в интервале рабочих температур было незначительным. Необходимо, чтобы эти сплавы способны были протягиваться в проволоку диаметром порядка сотых долей миллиметра. Среди них надо отметить следующие сплавы: манганин, константан, нихром.

1. Постоянный проволочный резистор

К наиболее распространенным постоянным проволочным резисторам относятся резисторы типов ПЭ (проволочные эмалированные), ПВЭ (проволочные эмалированные влагостойкие), ПЭВТ (проволочные эмалированные влагостойкие и термостойкие) и др. мощностью от 3 до 150 Вт.

Урок 10. МАРКИРОВКА РЕЗИСТОРОВ ВСЕХ ТИПОВ

По конструкции представляют собой керамический каркас, на который с шагом намотана неизолированная константановая либо нихромовая проволока. После намотки каркас покрывается защитным слоем стеклоэмали, которая изолирует друг от друга витки обмотки и защищает ее от влаги, загрязнений и механических повреждений. В зависимости от вида резистора, выводы от резистивного элемента выполняются в виде гибких жгутов, свитых из тонких медных проволок, либо латунных пластинок с отверстиями для подпайки внешних проводников схемы, либо пластинки из нержавеющей стали.

Конструкции постоянных проволочных резисторов приведены на рис. 2.1.

Рис. 2.2.1. Резисторы типа ПЭ (а), ПЭВ (б) и ПЭВР (в).

При относительно небольших размерах проволочные резисторы обладают высокой допустимой мощность рассеяния, высокой точностью и хорошей температурной стабильностью. Так как резисторы изготавливают путем намотки провода на каркас, то они имеют большую индуктивность и собственную емкость.

Для уменьшения индуктивности применяют бифилярную намотку, при которой обмотку резистора выполняют сдвоенным проводом, благодаря чему поля расположенных рядом витков направлены навстречу друг другу и вычитаются. Уменьшение индуктивности достигается так же путем намотки на плоский каркас. Недостатком бифилярной намотки является большая собственная емкость. Для получения малой индуктивности и емкости применяют разбивку обмотки на секции, в каждой из которых поочередно меняется направление намотки. Проволочные резисторы значительно дороже тонкопленочных, поэтому применяют их в тех случаях, когда характеристики тонкопленочных резисторов не удовлетворяют предъявленным требованиям.

2.3 Переменные проволочные резисторы

Переменные проволочные резисторы выполняются на тороидальных каркасах и трубчатых каркасах круглого, прямоугольного и квадратного сечения. В технологии производства переменных проволочных резисторов широко используются пластмассовые и керамические кольцевые каркасы, а также плоские каркасы из гетинакса и текстолита, которые после намотки свертываются в кольцо. Для равномерного соприкосновения скользящего контакта с обмоткой необходима плотная укладка провода с одинаковым усилием натяжения. Отечественная промышленность выпускает широкий ассортимент проволочных переменных резисторов.

На рис 2.3.1. представлены крепления переменных резисторов.

Рис 2.3.1. Крепления переменных резисторов

а – гайкой за штуцер; в,б – винтами; г,д – приклеиванием; е – групповой способ с помощью винтов и шпилек; ж,з – пайкой за выводы;

Для регулировки в электрических цепях электротехнических и радиотехнических устройств используют резисторы типов РП и ППБ.

Проводящие элементы этих резисторов получают из нихромового провода. Резисторы типа РП выполняются на керамических каркасах, резисторы типа ППБ выполняются бескаркасным способом. Конструкция резисторов ППБ контакта, узлы и детали ее прочны и позволяют применять прогрессивные технологические методы.

1. Резистивные материалы, материалы для проволочных резисторов

3.1. Резистивные материалы

В настоящее время проволочные резисторы изготавливаются с сопротивлением от сотых долей ома до мегаома и выше.

Резистивная проволока, применяемая в постоянных проволочных резисторах, должна иметь следующие основные свойства:

• Высокую стабильность сопротивления;
• Малый температурный коэффициент сопротивления;
• Высокую коррозионную устойчивость;

В таблице3.1.1. приведены резистивные материалы применяемые в постоянных и переменных проволочных резисторах.

Таблица 3.1.1. – Характеристики резистивных сплавов

Манганин – это медно-марганцевый сплав, состоящий из 83-86,5% меди, 11-13,5% марганца и 2,5-3,5% никеля. В большинстве случаев в проволочных резисторах используют эмалированные манганиновые провода марок ПЭМГ,ПЭММ. Манганиновая проволока выпускается марок: ПМТ – твердая, ПММ – мягкая, ПМС – стабилизированная.

Манганин можно легко получить в виде тонкой проволоки диаметром 0.02 мм. Малый ТКС и повышенная стабильность сопротивления во времени достигается путем термической обработки манганина – отжигом при температуре 650 — 800К в вакууме с последующим медленным охлаждением. Обладая высокой стабильностью сопротивления, низким ТКС, малой термо- э.д.с. по отношению к меди, манганиновая проволока широко используется в точных постоянных проволочных резисторах, работающих при температуры, близкой к нормальной.

Хромоникелевые сплавы (нихромы) используют для получения для получения проводящих элементов с повышенной термостойкостью. Нихром отличается значительной стойкостью к окислению на воздухе при высоких температурах. В результате нагрева на его поверхности образуется защитный слой устойчивых окислов NiO, Cr2O3 с температурным коэффициентом линейного расширения близким к коэффициенту сплава. При резких изменениях температуры происходит частичное разрушение слоя окислов, кислород проникает в трещины, вызывая дополнительное окисление. Поэтому при многократных кратковременных включениях проводящего элемента, выполненного из нихрома, под нагрузку его срок службы значительно меньше, чем при непрерывной электрической нагрузке.

В состав константана и нихрома входит большое количество дорогого металла – никеля. В некоторых случаях эти сплавы заменяют более дешевым – фехралем, основными компонентами которого являются железо, хром и алюминий. По сравнению с нихромом данный сплав более твердый, хрупкий и с трудом вытягивается в проволоку малого диаметра.

Одним из основных требований к сплавам, применяемым в технологии производства резисторов с повышенной точностью является высокая стабильность сопротивления во времени.

Высокое удельное сопротивление проволоки и их малый диаметр делают возможным создание миниатюрных высокоомных постоянных и переменных проволочных резисторов, отличающихся высокими технологическими характеристиками. Нихромовая проволока имеет высокую твердость и отличается большой износоустойчивостью, что позволяет применять ее для переменных резисторов с большим ресурсом работы.

Основным узлом любого проволочного резистора является резистивный элемент. Технологические характеристики резистора в значительно мере зависят от правильного выбора конструкции и материалов этого элемента. Обычно резистивный элемент состоит из каркаса и обмотки, к концам которой крепятся проводник, соединяющие ее с выводами резистора. Исключением являются бескаркасные резистивные элементы. Для резистивных элементов проволочных резисторов наиболее часто используются следующие виды обмоток:

• однослойная с фиксированным шагом;
• однослойная плотная;
• многослойная

На рисунке 3.2.1. представлены виды обмоток проволочных резисторов

Рисунок 3.2.1. – Виды обмоток проволочных резисторов

а — однослойная с фиксированным шагом; б – однослойная плотная;

в – многослойная; г – многослойная свободная.

3.3. Резистивные материалы на основе благородны х материалов

Оксидные пленки, которые образуются на поверхности проволок из сплавов на основе неблагородных металлов, являются причиной повышенных контактных сопротивлений в переменных проволочных резисторах. Под влиянием времени, воздействия повышенных температур и влажности контактные сопротивления могут резко возрастать, и в некоторых случаях это приводит к нарушению электрического контакта.

Проволоки из благородных материалов позволяют создавать низкоомные миниатюрные переменные резисторы с высокой электрической разрешающей способностью.

В таблице 3.3.1. представлены характеристики благородных сплавов применяемые в переменных проволочных резисторах.

Таблица 3.3.1. – Благородные сплавы

Продолжение таблицы 3.3.1.

Наиболее полно вышеперечисленн ым требованиям удовлетворяют благородные металлы или сплавы на их основе, характеристики которых приведены в таблице 3.3.1.

Платина и ее сплавы.

Платина имеет большое удельное электрическое сопротивление и низкую теплопроводность, не окисляется на воздухе, не тускнеет в любых условиях и легко поддается механической обработке. Однако вследствие малой твердости она редко применяется для скользящих контактов в чистом виде.

Наибольший интерес для скользящих контактов представляют сплавы платины с иридием и никелем. Платина-иридиевый сплав не окисляется, обладает высокой твердостью и механически меньше изнашивается, чем платина, допуская высокие контактные усилия. Для скользящих контактов в основном используются сплавы платины с 5—30% иридия.

Сплав платина-никель образует непрерывный ряд твердых растворов. Никель значительно повышает удельное сопротивление и твердость сплава. Сплавы платины с никелем пластичны и их легко обрабатывать. В качестве контактов наиболее известен сплав с 5% никеля, который обладает высокой коррозионной стойкостью и незначительно увеличивает свое контактное сопротивление при образовании сернистых пленок.

Иногда для скользящих контактов используют сплав платины с 14% рутения. Рутений вдвое повышает твердость сплава по сравнению с иридием. Однако при нагревании в воздухе рутений окисляется, и сплав теряет в весе вследствие улетучиваемых окислов рутения.

Необходимо отметить, что платина и ее сплавы склонны к образованию игл и мостиков при малых токах.

Палладий и его сплавы.

Среди металлов платиновой группы палладий является наиболее перспективным материалом для контактов. По стоимости палладий в 4—5 раз дешевле платины, а по многим свойствам очень близок к ней, заметная разница имеется только в температуре плавления. На Воздухе палладий тускнеет быстрее платины, но окислы его нестойки и при температуре свыше 350°С быстро разлагаются.

Палладий стоек к образованию сульфидных пленок. Чистый палладий идет на покрытия для скользящих контактов, работающих при небольших контактных усилиях. Сплавы палладия с серебром, иридием широко применяются для маломощных скользящих контактов. В сплаве палладий оказывает защитное действие по отношению к серебру.

При наличии палладия (более 50%) сплав стоек к образованию сернистых пленок. Серебряно-палладиевые сплавы пластичны и хорошо поддаются механической обработке. Большое распространение для скользящих контактов малогабаритных резисторов получил сплав палладия, серебра (36%) и меди

Источник: www.yaneuch.ru

Задание №12 ОГЭ по физике |

В задании № 12 ОГЭ по физике необходимо понимание явления постоянного тока, процессов, протекающих в цепях постоянного эл.тока, и знание формул, описывающих такие процессы количественно. Полезные сведения, которые могут потребоваться для решения задания, приведены в разделе теории.

Теория к заданию №12 ОГЭ по физике

Сопротивление цилиндрического проводника

Цилиндрическим считается проводник, имеющий круг в поперечном сечении. Сопротивление такого проводника может быть найдено из уравнения:

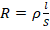
где ρ – удельное эл.сопротивление, индивидуально характерное для различных материалов; l – длина проводника; S – площадь его поперечного сечения.

Последовательное и параллельное соединение проводников

Последовательное соединение:

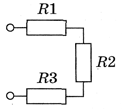
При последовательном соединении сопротивления и напряжения на каждом из резисторов суммируются. Сила тока при этом является неизменной на всех участках разветвления.

Математически это выражается формулами:

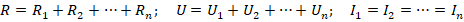
Параллельное соединение:

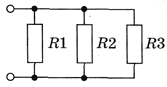
При параллельном соединении суммируются, наоборот, силы тока на каждом из участков. Неизменным при этом остается напряжение. А общее сопротивление определяется по особой формуле.

Математически это выглядит так:

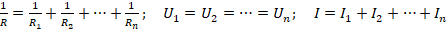
Заряд в проводнике

В проводнике движутся электроны. Эл.ток возникает при их упорядоченном (т.е. направленном) перемещении с какой-то скоростью. Интерес в данном случае представляет величина заряда, который проходит через поперечное сечение данного проводника за определенное время ∆t. Вычислить эту величину можно по формуле:

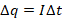
Мощность электрической цепи

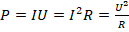
Эту величину можно рассчитать по одной из нескольких формул:

где I – сила тока на исследуемом участке эл.цепи; U – напряжение на этом участке; R – сопротивление.

То или иное уравнение для вычислений следует выбирать в зависимости от известных в условии задачи данных.

Закон Джоуля–Ленца

Когда под воздействием эл.поля в цепи не происходит хим.преобразования вещества и не совершается механическая работа, то работа, производимая эл.полем, ведет только к нагреву проводника. Кол-во теплоты, которое при этом выделяет проводник с эл.током, равно:

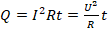
где t – время, в течение которого совершается работа.

Разбор типовых вариантов заданий №12 ОГЭ по физике

Демонстрационный вариант 2018

[su_note note_color=”#defae6″]

На рисунке изображена схема электрической цепи, состоящей из трёх резисторов и двух ключей К1 и К2. К точкам А и В приложено постоянное напряжение. Максимальное количество теплоты, выделяемое в цепи за 1 с, может быть получено

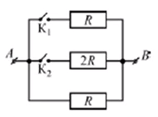
1. если замкнут только ключ К1
2. если замкнут только ключ К2
3. если замкнуты оба ключа
4. если оба ключа разомкнуты

Алгоритм решения:

1. Анализируем схему, приведенную в условии. Определяем расчетную формулу.

2–5. Определяем кол-во теплоты в каждой из ситуаций, рассмотренных в утверждениях 1–4. Определяем прав.вариант ответа.

Решение:

1. По з-ну Джоуля-Ленца 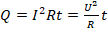. Поскольку имеет место параллельное соединение разных резисторов, то сила тока в каждой ветке будет различаться. А напряжение при этом во всех ветках одинаково. Поэтому в данном случае удобнее воспользоваться 2-й формулой (в которой присутствует напряжение).
2. Рассм.утверждение 1. Здесь ток будет протекать по двум параллельным веткам – верхней и нижней. Общее сопротивление при этом равно: 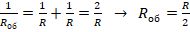. Тогда за 1 с .
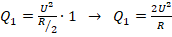3. В утверждении 2 замкнули ключ 2. Следовательно, ток течет по средней и нижней веткам. В этом случае 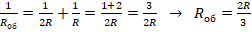. Искомое кол-во теплоты: .
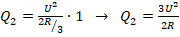4. Если оба ключа замкнуть, то ток потечет по всем 3 веткам. Отсюда: 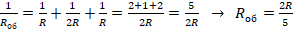. Кол-во теплоты за 1 с в таком случае составит: .
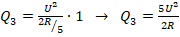5. В утверждении 4 рассмотрен вариант, когда оба ключа разомкнуты. Это означает, что ток течет только по нижней ветке и .
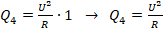6. Сравним полученные кол-ва теплоты. Сравнивать будем с Q4, поскольку полученная для этой величины формула не содержит коэффициента. Итак: 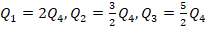. Отсюда видно, что, во-первых, каждое из Q1–Q3 больше, чем Q4, а во-вторых, среди этих трех значений самое большое имеет Q3. Т.е. максимальное кол-во теплоты выделится, если замкнуть оба ключа.

Первый вариант (Камзеева, № 3)

[su_note note_color=”#defae6″]

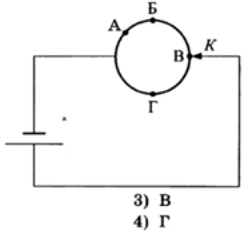
Из однородной металлической проволоки сделано кольцо. Напряжение на полюсах источника тока постоянно. При каком подключении контакта К потребляемая мощность цепи будет минимальной?

Алгоритм решения:

1. Записываем формулу для расчета мощности через напряжение и сопротивление. Определяем условие, при котором она будет минимальной.
2. Находим зависимость сопротивления от длин проводников.
3. Анализируем особенность параллельного соединения проводников и, исходя из этого и выводов п.2, определяем точку подключения ключа.

Решение:

1. По условию напряжение на источнике тока является постоянной величиной. Поэтому для расчета мощности удобнее всего воспользоваться такой формулой: 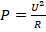. Из этой формулы следует, что минимальная мощность будет в точке, в которой максимально сопротивление.
2. Сопротивление цилиндрического проводника вычисляется по формуле: 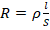. Поскольку проволока однородна, то ρ в данном случае есть величина постоянная. Постоянна и S, т.к. длина кольца не меняется. Поэтому сопротивление здесь пропорционально длине проводника l. Тогда имеем зависимость: чем больше длина проводника, тем больше сопротивление.
3. Из схемы цепи видно, что в любом случае соединение проводников будет параллельным. А потому тут следует помнить еще один момент: при параллельном соединении проводников общее сопротивление всегда будет меньше самого меньшего из сопротивлений (что можно проверить опытным путем). Самое маленькое сопротивление у проводника А, т.к. у него наименьшая длина (см.п.2). Поэтому в данном случае ключ нужно подключить в точку, которая является самой удаленной от А. Ею является т.В. Именно так получим максимальное сопротивление и, соответственно (см.п.1), минимальную мощность цепи.

Второй вариант (Камзеева, № 5)

[su_note note_color=”#defae6″]

На рисунке показано подключение в сеть постоянного напряжения трех одинаковых ламп.

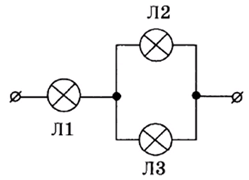
С минимальным накалом будет(-ут) гореть лампа(-ы)

Алгоритм решения:

1. Записываем формулу для расчета эл.мощности ламп через силу тока и сопротивление.
2. Анализируем приведенную в условии схему и определяем зависимость мощности от силы тока и сопротивления.
3. Определяем мощность каждой из ламп, сравниваем их.

Решение:

1. Степень накала ламп зависит от величины тепловой мощности, выделяемой на каждой из них. Для определения электрической мощности используем формулу .
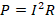2. Сопротивления у ламп равны между собой, т.к. лампы одинаковы. А сила токов будет различаться на участке Л1 и на участке параллельного соединения ламп Л2 и Л3. При параллельном соединении ток делится, причем, поскольку лампы одинаковы, то ток разделится поровну. Т.е. если принять, что через Л1 идет ток I, то через Л2 и Л3 – токи, равные I/2.
3. Мощность лампы Л1 будет равной 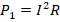, мощности Л2 и Л3 – 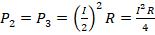. Из этих формул видно, что мощность ламп Л2 и Л3 в 4 раза меньше, чем Л1. Этой ситуации соответствует ответ №4.

Третий вариант (Камзеева, № 10)

[su_note note_color=”#defae6″]

Четыре резистора изготовлены из различных материалов и имеют различные размеры (см. рис.).

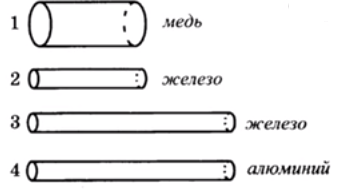
Наибольшее электрическое сопротивление имеет резистор

Алгоритм решения:

1. Запишем формулу для вычисления эл.сопротивления цилиндрического проводника.
2. Находим соотношение длин разных проводников.
3. Определяем соотношение у разных проводников площадей поперечного сечения.
4. Определяем соотношения между уд.сопротивлениями.
5. Находим сопротивление для каждого проводника, сравниваем их величины. Определяем максимальное сопротивление.

Решение:

1. Поскольку на рисунке изображены цилиндрические проводники, то для определения их сопротивлений можно использовать формулу .
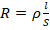2. Поскольку сопротивление пропорционально длине проводника, то это значит, что чем больше длина, тем больше сопротивление. Этому условию отвечают проводники 3 и 4. Из рисунка видно, что они приблизительно в 2 раза длиннее, чем 1 и 2. Т.е. если принять, что l1=l2=l, то тогда l3=l4=2l.
3. С площадью все наоборот: чем она больше, тем сопротивление меньше. Поэтому с этой точки зрения менее всего подходит 1-й проводник. У него диаметр (и, соответственно, радиус) примерно в 2 раза больше, чем у остальных; а это означает, что его площадь сечения примерно в 4 раза больше. И если принять, что S2=S3=S4=S, то S1=4S.
4. 3-й параметр, который тут необходимо участь, – удельное сопротивление (эти значения следует смотреть в соответствующей таблице). Для меди оно равно 0,017 (Ом·мм 2 /м), для железа – 0,10, для алюминия – 0,028. Соотнесем эти величины с самой маленькой из них – 0,017, обозначив ее ρ. Сравнение дает такие результаты: уд.сопротивление у железа 5,88ρ, а у алюминия – 1,65ρ.
5. Делаем общий вывод. Для 1-го проводника 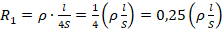. Для 2-го проводника 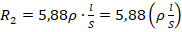. Для 3-го проводника 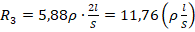. Для 4-го проводника 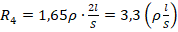. Отсюда видно, что максимальное сопротивление имеет проводник 3.

Источник: spadilo.ru

2.5. Электрическое сопротивление. Удельное электрическое сопротивление

Электрическое сопротивление характеризует способность проводника противодействовать прохождению по нему электрического тока. Не следует думать, что из вышеприведенной формулы следует, что электрическое сопротивление зависит от приложенного напряжения и силы тока. Электрическое сопротивление зависит от материала проводник, его длины и площади поперечного сечения, что выражается формулой

где $l$ — длина проводника, $s$- площадь его поперечного сечения, а $rho $ — удельное электрическое сопротивление, оно характеризует из какого вещества изготовлен проводник. Единица измерения удельного электрического сопротивления в системе СИ — Ом · м, но на практике при расчетах пользуются другой единицей измерения — (Ом · мм 2 )/м.

Решение заданий Открытого банка заданий ФИПИ

1. Установите соответствие между физическими величинами и единицами этих величин в системе СИ: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

Б) электрическое сопротивление

Запишите в таблицу выбранные цифры под соответствующими буквами.

Нажмите, чтобы увидеть решение

Единица измерения напряжения — вольт (В), сопротивления — ом (Ом), электрического заряда — кулон (Кл).

2. Установите соответствие между физическими величинами и приборами, предназначенными для измерения этих величин. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Б) электрическое напряжение

Нажмите, чтобы увидеть решение

Прибор для измерения электрического заряда — электрометр, напряжения — вольтметр, сопротивления — омметр.

3. В справочнике физических свойств различных материалов представлена следующая таблица.

Вещество	Плотность в твёрдом состоянии, г/см 3	Удельное электрическое сопротивление (при 20 °С), Ом⋅мм 2 /м
Железо	7,8	0,1
Константан (сплав)	8,8	0,5
Латунь	8,4	0,07
Никелин (сплав)	8,8	0,4
Нихром (сплав)	8,4	1,1
Серебро	10,5	0,016

Используя данные таблицы, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) При равных размерах самым лёгким окажется проводник из серебра.
2) При равных размерах самое маленькое электрическое сопротивление имеет проводник из серебра.
3) Проводники из латуни и нихрома одинакового размера имеют одинаковую массу, но разные электрические сопротивления.
4) Чтобы при равной длине проводник из железа имел одинаковое электрическое сопротивление с проводником из никелина, он должен иметь в 4 раза большую площадь поперечного сечения.
5) При равной площади поперечного сечения проводник из константана длиной 5 м имеет такое же электрическое сопротивление, как и проводник из никелина длиной 4 м.

Нажмите, чтобы увидеть решение

Утверждение 1 — неверно. Серебро имеет самую большую плотность из представленных веществ, поэтому он будет иметь при равных размерах самую большую массу;

Утверждение 2 — верно. Серебро обладает самым малым удельным сопротивлением, значит при равных размерах проводник из серебра будет иметь самое маленькое сопротивление;

Утверждение 3 — верно. У латуни и нихрома одинаковая плотность, значит при одинаковых размерах проводники будут иметь одинаковую массу. У латуни и нихрома разные значения удельного сопротивления, значит при одинаковых размерах проводники будут иметь разные сопротивления;

Утверждение 4 — неверно. Пусть $R_1$ — сопротивление железного проводника, $rho _1,; l_1,; s_1$ — его удельное сопротивление, длина и площадь сечения соответственно. Тогда $R_2$ — сопротивление никелинового проводника, $rho _2,; l_2,; s_2$ — его удельное сопротивление, длина и площадь сечения соответственно. Из равенства сопротивлений, а также, учитывая, что $l_1=l_2$ и $rho _2=4rho _1$ (см. таблицу значений), получаем

Проводник из никелина должен иметь площадь сечения в 4 раза большую.

Утверждение 5 — неверно. Пусть $R_1$ — сопротивление проводника из константана, $rho _1,; l_1,; s_1$ — его удельное сопротивление, длина и площадь сечения соответственно. Тогда $R_2$ — сопротивление никелинового проводника, $rho _2,; l_2,; s_2$ — его удельное сопротивление, длина и площадь сечения соответственно. Сравним сопротивления, учитывая, что $s_1=s_2$

Сопротивление константанового проводника больше.

4. Необходимо экспериментально обнаружить зависимость электрического сопротивления круглого проводящего стержня от материала, из которого он изготовлен. Какую из указанных пар стержней (см. рисунок) можно использовать для этой цели?

1) А и Г
2) Б и В
3) Б и Г
4) В и Г

Нажмите, чтобы увидеть решение

Сопротивление проводника зависит от материала проводника, его длины и площади поперечного сечения. Так как мы исследуем зависимость сопротивления от материала, то материал двух стержней должен быть разным, а площадь сечения и длина одинаковы. Таких пар две — А и Б, В и Г.

5. В таблице приведены результаты экспериментальных измерений площади поперечного сечения S, длины L и электрического сопротивления R для трех проводников, изготовленных из железа или никелина.

Материал проводника	S, мм 2	L, м	R, Ом
Проводник №1	Железо	1	1	0,1
Проводник №2	Никелин	2	3	0,6
Проводник №3	Никелин	1	1	0,4

На основании проведенных измерений можно утверждать, что электрическое сопротивление проводника

1) зависит от материала проводника
2) не зависит от материала проводника
3) увеличивается при увеличении его длины
4) уменьшается при увеличении площади его поперечного сечения

Нажмите, чтобы увидеть решение

Сопротивление проводника зависит от материала проводника, его длины и площади поперечного сечения. Второй вариант ответа априори не правильный. Если проверять зависимость сопротивления проводника от длины или площади, то нужно взять проводники из одного материала (№2 и №3).

Но проверить эти зависимости не получится, т.к. в таком случае либо площадь, либо длина должны быть одинаковы. Таких значений в таблице нет. Если исследовать зависимость сопротивления от материала, то материал двух стержней должен быть разным, а площадь сечения и длина одинаковы. Таким условиям удовлетворяют проводники №1 и №3, причем сопротивление этих проводников различно. Значит, на основании проведенных измерений можно утверждать, что электрическое сопротивление проводника зависит от материала проводника.

6. Металлическую пластинку со сторонами a×2a×3a подключают к источнику постоянного напряжения так, как показано на рисунке 1.

Считая, что ток равномерно распределён по сечению пластинки, определите, как изменятся физические величины: электрическое сопротивление пластины и сила протекающего через пластину тока при подключении этой пластинки к тому же источнику напряжения так, как показано на рисунке 2. Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Электрическое сопротивление пластинки

Сила электрического тока, протекающего через пластинку

Нажмите, чтобы увидеть решение

Найдем отношение сопротивлений пластинок

сопротивление второй пластинки больше в 9 раз. Так как сопротивление увеличилось, то сила тока при постоянном напряжении уменьшится.

7. Электрическая плитка при силе тока 6 А за 120 с потребляет 108 кДж энергии. Чему равно сопротивление спирали плитки?

Нажмите, чтобы увидеть решение

Найдем электрический заряд, прошедший через спираль плитки

$q=ItRightarrow q=6cdot 120=720$ Кл.

Теперь найдем напряжение, подаваемое на плитку

Рассчитаем сопротивление плитки

8. Определите плотность никелиновой проволоки площадью поперечного сечения 1 мм 2 и массой 176 г, из которой изготовлен реостат, если при напряжении на его концах 24 В сила протекающего тока равна 3 А.

Нажмите, чтобы увидеть решение

Чтобы определить плотность проволоки необходимо знать массу и объем проволоки

Объем проволоки связан с длиной проволоки и ее площадью сечения соотношением $V=sl$. Площадь сечения известна, найдем длину проволоки. Используем для этого формулу расчета сопротивления проводника

где $lambda $ — удельное сопротивление никелина (обозначение взято для того, чтобы отличить удельное сопротивление от плотности). Рассчитаем сопротивление проводника

$V=1cdot 10^cdot 20=20cdot 10^$ м 3 ,

Ответ: 8800 кг/м 3 .

9. Исследуя зависимость силы тока от напряжения на резисторе при его постоянном сопротивлении, ученик получил результаты, представленные в таблице. Чему равно удельное сопротивление металла, из которого изготовлен резистор, если длина провода 25 м, а площадь его поперечного сечения 1 мм 2 ?

Источник: www.fizika-online.ru