Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).
Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:
группа I — обозначения геометрических фигур и отношений между ними;
группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.
Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ
А. Обозначение геометрических фигур
1. Геометрическая фигура обозначается — Ф.
Что такое знак СУММЫ и как он работает?
2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:
А, В, С, D, . , L, М, N, .
3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
а, b, с, d, . , l, m, n, .
Линии уровня обозначаются: h — горизонталь; f— фронталь.
Для прямых используются также следующие обозначения:
(АВ) — прямая, проходящая через точки А а В;
[АВ) — луч с началом в точке А;
[АВ] — отрезок прямой, ограниченный точками А и В.
4. Поверхности обозначаются строчными буквами греческого алфавита:
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α(а || b) — плоскость α определяется параллельными прямыми а и b;
β(d1 d2gα) — поверхность β определяется направляющими d1 и d2 , образующей g и плоскостью параллелизма α.
5. Углы обозначаются:
∠ABC — угол с вершиной в точке В, а также ∠α°, ∠β°, . , ∠φ°, .

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри
7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.
|АВ| — расстояние между точками А и В (длина отрезка АВ);
|Аа| — расстояние от точки А до линии a;
|Аα| — расстояшие от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| расстояние между поверхностями α и β.
8. Для плоскостей проекций приняты обозначения: π1 и π2, где π1 — горизонтальная плоскость проекций;
π2 —фрюнтальная плоскость проекций.
ФОКУС с треугольником #shorts
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т. д.
9. Оси проекций обозначаются: х, у, z, где х — ось абсцисс; у — ось ординат; z — ось аппликат.
Постояшную прямую эпюра Монжа обозначают k.
10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:
А’, В’, С’, D’, . , L’, М’, N’, горизонтальные проекции точек; А», В», С», D», . , L», М», N», . фронтальные проекции точек; a’ , b’ , c’ , d’ , . , l’, m’ , n’ , — горизонтальные проекции линий; а» ,b» , с» , d» , . , l» , m» , n» , . фронтальные проекции линий; α’, β’, γ’, δ’. ζ’,η’,ν’. горизонтальные проекции поверхностей; α», β», γ», δ». ζ»,η»,ν». фронтальные проекции поверхностей.
11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса 0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
Так: h0α — горизонтальный след плоскости (поверхности) α;
f0α — фронтальный след плоскости (поверхности) α.
12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: Ha — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии ) a.
13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,2,3. n:
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :
А 0 , В 0 , С 0 , D 0 , .
1 0 , 2 0 , 3 0 , 4 0 , .
a 0 , b 0 , c 0 , d 0 , .
α 0 , β 0 , γ 0 , δ 0 , .
15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :
А 1 0 , В 1 0 , С 1 0 , D 1 0 , .
1 1 0 , 2 1 0 , 3 1 0 , 4 1 0 , .
a 1 0 , b 1 0 , c 1 0 , d 1 0 , .
α 1 0 , β 1 0 , γ 1 0 , δ 1 0 , .
Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.
| 1 | ≡ | Совпадают | (АВ)≡(CD) — прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки С и D |
| 2 | ≅ | Конгруентны | ∠ABC≅∠MNK — угол АВС конгруентен углу MNK |
| 3 | ∼ | Подобны | ΔАВС∼ΔMNK — треугольники АВС и MNK подобны |
| 4 | || | Параллельны | α||β — плоскость α параллельна плоскости β |
| 5 | ⊥ | Перпендикулярны | а⊥b — прямые а и b перпендикулярны |
| 6 | 
|
Скрещиваются | с  d — прямые с и d скрещиваются d — прямые с и d скрещиваются |
| 7 |  |
Касательные | t  l — прямая t является касательной к линии l. l — прямая t является касательной к линии l. β  α — плоскость β касательная к поверхности α α — плоскость β касательная к поверхности α |
| 8 | → | Отображаются | Ф1→Ф2 — фигура Ф1 отображается на фигуру Ф2 |
| 9 | S | Центр проецирования. Если центр проецирования несобственная точка, то его положение обозначается стрелкой, указывающей направление проецирования |
— |
| 10 | s | Направление проецирования | — |
| 11 | P | Параллельное проецирование | рs α Параллельное проецирование — параллельное проецирование на плоскость α в направлении s |
| 1 | M,N | Множества | — | — |
| 2 | A,B,C. | Элементы множества | — | — |
| 3 | Состоит из . | Ф | Ф — фигура Ф состоит из точек А, В,С, . | |
| 4 | ∅ | Пустое множество | L — ∅ — множество L пустое (не содержит элементов ) | — |
| 5 | ∈ | Принадлежит, является элементом | 2∈N (где N — множество натуральных чисел) — число 2 принадлежит множеству N |
А ∈ а — точка А принадлежит прямой а (точка А лежит на прямой а ) |
| 6 | ⊂ | Включает, cодержит | N⊂М — множество N является частью (подмножеством) множества М всех рациональных чисел |
а⊂α — прямая а принадлежит плоскости α (понимается в смысле: множество точек прямой а является подмножеством точек плоскости α) |
| 7 | ∪ | Объединение | С = A U В — множество С есть объединение множеств A и В; = ∪ |
ABCD = [AB] ∪ [ВС] ∪ [CD] — ломаная линия, ABCD есть объединение отрезков [АВ], [ВС], [CD] |
| 8 | ∩ | Пересечение множеств | М=К∩L — множество М есть пересечение множеств К и L (содержит в себе элементы, принадлежащие как множеству К, так и множеству L). М ∩ N = ∅— пересечение множеств М и N есть пустое множество (множества М и N не имеют общих элементов) |
а = α ∩ β — прямая а есть пересечение плоскостей α и β а ∩ b = ∅ — прямые а и b не пересекаются (не имеют общих точек) |
| 1 | ∧ | Конъюнкция предложений; соответствует союзу «и». Предложение (р∧q) истинно тогда и только тогда,когда р и q оба истинны |
α∩β = < К:K∈α∧K∈β>Пересечение поверхностей α и β есть множество точек (линия), состоящее из всех тех и только тех точек К, которые принадлежат как поверхности α, так и поверхности β |
| 2 | ∨ | Дизъюнкция предложений; соответствует союзу «или». Предложение (p∨q) истинно, когда истинно хотя бы одно из предложений р или q (т. е. или р, или q, или оба). |
— |
| 3 | ⇒ | Импликация — логическое следствие. Предложение р⇒q означает: «если р, то и q» | (а||с∧b||с)⇒a||b. Если две прямые параллельны третьей, то они параллельны между собой |
| 4 | ⇔ | Предложение (р⇔q) понимается в смысле: «если р, то и q; если q, то и р» | А∈α⇔А∈l⊂α. Точка принадлежит плоскости, если она принадлежит некоторой линии, принадлежащей этой плоскости. Справедливо также и обратное утверждение: если точка принадлежит некоторой линии, принадлежащей плоскости, то она принадлежит и самой плоскости |
| 5 | ∀ | Квантор общности, читается: для всякого, для всех, для любого. Выражение ∀(x)P(x) означает: «для всякого x: имеет место свойство Р(х) « |
∀( ΔАВС)( 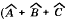 = 180°) Для всякого (для любого) треугольника сумма величин его углов = 180°) Для всякого (для любого) треугольника сумма величин его углов при вершинах равна 180° |
| 6 | ∃ | Квантор существования, читается: существует. Выражение ∃(х)P(х) означает: «существует х, обладающее свойством Р(х)» |
(∀α)(∃a)[a⊄α∧a||α].Для любой плоскости α существует прямая а, не принадлежащая плоскости α и параллельная плоскости α |
| 7 | ∃1 | Квантор единственности существования, читается: существует единственное (-я, -й). Выражение ∃1(x)(Рх) означает: «существует единственное (только одно) х, обладающее свойством Рх» |
(∀ А, В)(А≠B)(∃1а)(а∋А, В) Для любых двух различных точек А и В существует единственная прямая a, проходящая через эти точки. |
| 8 | (Px) | Отрицание высказывания P(x) | а b( ∃α )(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их
b( ∃α )(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их |
| 9 | Отрицание знака | [AB]≠[CD] —отрезок [АВ] не равен отрезку [CD].а?b — линия а не параллельна линии b |
Источник: nachert.ru
Знак дельта и его значение. Знак дельта в «Ворде»
Достаточно часто приходится в процессе набора различных документов вводить нам знак дельта. Именно его значение, а также способы ввода в различных приложениях под управлением такой ОС, как «Виндовс», и будут рассмотрены в этой статье.

Откуда он пришел?
Сам знак дельта пришел к нам из греческого языка. Это одна из букв его алфавита. На сегодняшний день ученые считают, что она послужила прародителем латинской буквы D, которая присутствует в большинстве алфавитов стран Европы и не только. В нашем же языке ее аналогом является «Д».
Большой символ данной буквы – это равнобедренный треугольник, у которого в основании расположена самая маленькая сторона (то есть «Δ»). В свою очередь, прописной буквой является маленький круг с характерным верхним хвостиком (он выглядит так: «δ»). Чуть позже эти символы начали активно использоваться в различных сферах человеческой жизни, среди которых можно выделить математику и географию.
География
Широко используется данное понятие в географии. Здесь под этим термином скрывается область впадения реки в море или океан. Сверху она выглядит как треугольник. То есть аналогия здесь налицо, и подобное определение в этом случае более чем оправданно. Наиболее яркие примеры – это реки Нил (впадает в Средиземное море в северной части Африканского континента) или Амазонка (впадает в Атлантический океан и расположена в Южной Америке). С высоты птичьего полета места на стыке суши и воды этих двух великих рек действительно выглядят, как греческая буква Δ.

Математика
Значительно чаще и больше используется знак дельта в математике. Здесь он может обозначать следующее:
- Приращение аргументов. То есть за этим понятием скрывается величина, на которую изменилась переменная. Например, 2+3=5. В этом случае 2 увеличилась на 3. Это и есть Δ.
- Еще один случай, при котором используется эта буква греческого алфавита, – оператор Лапласа.
- Последний вариант, при котором используется Δ, — это обозначение определителя матрицы.
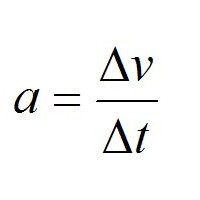
Это все справедливо для заглавной буквы. А вот с прописным символом ситуация аналогичная. Он может обозначать такое:
- В обозначении производной: δy/δx (аналогичным образом производная выглядит в физике, астрономии и космогонии).
- При описании дельта-функции, которая может быть равна бесконечности при аргументе ноль и нулю при всех остальных его значениях.
- С ее помощью обозначается символ Кронекера — δij. Он равен единице при равенстве индексов и нулю во всех остальных случаях.
В общем, не так уж и редко в современной математике можно встретить этот символ.
Физика
Еще одна сфера, где эта греческая буква повсеместно используется, — это физика. Большая часть величин этой науки связаны между собой в виде интегралов и производных. Например, скорость — это отношение δS к δt, то есть пройденного расстояния ко времени, за которое оно преодолено. В свою очередь, производной второго порядка от скорости по времени будет ускорение. Это лишь один из примеров, который показывает то, насколько важна эта греческая буква для современной физики.
Астрономия и космогония
Не меньшее значение греческая δ имеет и для этих наук. Здесь опять-таки многие величины взаимосвязаны между собой с помощью интегралов и производных. Именно последнее понятие и обозначается прописной буквой дельта.
Вводим в «Ворде»
Наиболее просто вставить в текст документа знак дельта в «Ворде» — с него и начнем. В первом случае в открытом окне данного приложения необходимо перейти на вкладку «Вставка» главного меню. Затем находим пункт с надписью «Символы». В нем открываем выпадающий список «Символ» (рядом с ним нарисована буква «омега», она по виду напоминает подкову).
В нем выбираем пункт «Другие символы» (расположен в самой нижней части этого списка). Затем путем перемещения по таблице всех доступных для ввода знаков находим нужный из них и вставляем в рабочую область приложения. Затем закрываем ранее открытое окно.
Второй вариант в текстовом процессоре «Ворд» основан на использовании редактора формул. Порядок набора в этом случае идентичный. Разница состоит лишь в том, что в пункте «Символы» выбираем не выпадающий список «Символ», а перечень «Формула». Затем выбираем пункт «Новая формула». Потом на месте главного меню появится панель «Конструктор».
В ее разделе находим подраздел «Символы». Затем, перемещаясь по нему, находим Δ (для заглавной буквы) или δ (в случае прописной). Потом с помощью клавиши «Таб» или указателя мыши нажимаем кнопку с надписью «Вставить». Далее закрываем окно вставки. В рабочей области текстового процессора должен появиться нужный нам символ.
Любое приложение
Можно набрать знак дельта на клавиатуре. Для этого нужно использовать АСКИ – код данного символа, который равен 916. Этот способ универсален и работает во всех приложениях под управлением ОС «Виндовс». Порядок набора в этом случае следующий:
- Переключаем язык ввода на английский.
- Переводим расширенную клавиатуру из режима навигации в режим ввода чисел. Для этого нажимаем клавишу «Нам Лук» до тех пор, пока ее светодиод не загорится.
- Переводим курсор в ту область приложения, в которой нужно набрать Δ с применением манипулятора.
- Зажимаем «Alt» в левой части клавиатуры.
- На следующем этапе необходимо ввести последовательно набор чисел, соответствующий символу дельта. Код знака у него — 916, как было отмечено ранее. Поэтому и набираем сразу 9, затем 1 и в конце 6.
- Отпускаем ранее зажатую клавишу «Alt». После этого в рабочей области нашего приложения должен появиться необходимый нам символ.
Кстати, можно код знака дельта в «Ворде» выяснить, если вы не знаете или забыли. Для этого достаточно по ранее приведенной методике зайти в окно вставки символа, найти в нем Δ, выделить его. В нижней части в поле «Код знака» и будет указана интересующая нас информация. Причем так можно узнать этот параметр для любого символа.
Этот же метод ввода можно использовать и при наборе прописной буквы. Единственное отличие – это то, что у нее код 948. То есть вместо 916 нужно этот порядок чисел применить. Минус данного способа состоит в том, что необходимо помнить АСКИ-коды. Если цифр в нем от одного до трех, то еще можно запомнить.
А при большем количестве символов этот метод уже не эффективно использовать.

Альтернативный вариант – буфер обмена
Еще один способ – это использовать буфер обмена, для того чтобы вставить «дельта». Знак треугольник нужно найти в любом приложении (например, на любом интернет–ресурсе). Выделить его с помощью манипулятора. Затем используется комбинация клавиш «Ctrl» и «Insert» (выполняем операцию копирования).
Переходим в то приложение, в котором нужно этот символ вставить (можно использовать комбинацию «Alt» и «Tab» или указатель мышки). Затем нажимаем «Shift» и «Insert» (выполняем операцию вставки). После этого справа от курсора должен появиться символ Δ. Аналогичным образом можно вставить и прописную букву. Минус этого способа состоит в том, что нужен исходный знак.
А не всегда есть возможность его найти. Поэтому это можно сделать только на компьютерах, которые подключены к глобальной паутине. В ней легко и просто можно найти исходный символ. В остальных случаях этот способ не рационально использовать.

Таблица символов: оптимальное решение в любом случае
Не всегда инсталлирован на компьютере текстовый процессор «Ворд». ЭВМ может быть не подключена к глобальной паутине и копировать знак дельта просто неоткуда. А АСКИ-код этого символа не помним. Как бы получается безвыходная ситуация. Но решение есть. Причем очень простое.
Достаточно использовать такую стандартную утилиту, как «Таблица символов». Для этого выполняем следующие манипуляции:
- Открываем меню «Пуск» с помощью нажатия соответствующей клавиши или кликом правой кнопки манипулятора типа мышь.
- В открывшемся списке необходимо выбрать пункт «Программы».
- На следующем этапе кликаем на надписи «Стандартные».
- Далее нужен раздел «Системные».
- Тут находим утилиту с надписью «Таблица символов».
- В списке находим нужную нам букву (заглавную Δ или прописную δ).
- Затем совершаем клик правой кнопкой мышки на кнопке «Выбрать». После этого должна активной стать другая кнопка – «Копировать». Ее и нажимаем. Затем выбранный нами символ помещается в буфер обмена.
- Далее переходим в то приложение, в котором необходимо вставить такой символ и нажимаем стандартную комбинацию «Ctrl» и «V». В качестве альтернативы можно использовать «Shift» и «Insert». Еще один способ вставки – это использование меню «Вставка» и одноименной кнопки.
В отличие от всех ранее приведенных методов, этот является универсальным и работает во всех программах под управлением такой операционной системы, как «Виндовс».

Подведем итоги: какой способ лучше?
Очень часто в процессе набора формул в математике, физике, астрономии и космогонии используется знак дельта, как заглавный, так и прописной. Поэтому важно его вводить именно в электронном виде документа. Проще всего вставить знак дельта в «Ворде» с помощью закладки «Вставка» и подпанельки «Вставка символа». Но это частный случай, и работает он только в этом текстовом процессоре.
В остальных случаях наиболее рационально использовать «Таблицу символов». При этом нет необходимости помнить специальные трехзначные АСКИ-коды или искать исходную букву, как в случае с буфером обмена. Тем более что эта утилита автоматически инсталлируется на все ПК в процессе установки операционной системы «Виндовс».
Источник: fb.ru
Треугольник
Треугольник – это фигура, состоящая из трех точек и трех отрезков, при этом три точки не лежат на одной прямой, а три отрезка попарно эти точки соединяют. Если быть точнее, то точки треугольника называются его вершинами, а отрезки – сторонами. Обозначается треугольник его вершинами, а вместо длинного слова треугольник рисуют символ Δ.
Давайте теперь подробнее рассмотрим разновидности треугольников.
- Равнобедренный треугольник – это такой треугольник, который имеет две одинаковые стороны, которые еще называют боковыми, третья сторона, отличная от тех двух, называется основанием.
- Равносторонний треугольник – треугольник с одинаковыми сторонами, также его иногда называют правильным треугольников.
- Прямоугольный треугольник – треугольник, который имеет прямой угол (90 градусов).
- Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90 градусов).
- Тупоугольный треугольник – треугольник, у которого один из углов тупой (то есть больше 90 градусов).
В принципе запомнить особенности каждого из вида треугольников легко, так каких названия говорят сами за себя.
Возьмем, к примеру, треугольник АВС. А, В, С являются его вершинами, а АВ, ВС и АС -соответственно его стороны.
Теперь рассмотрим строение данного треугольника более подробно. Угол треугольника АВС при вершине А – это угол, который образовался полупрямыми АВ и АС. Аналогично мы можем определить углы, которые лежат при вершине В и при вершине С.
Высота треугольника – это перпендикуляр, который опускается из заданной вершины к прямой, которая противоположна вершине.
Биссектриса треугольника – это отрезок биссектрисы угла данного треугольника, который соединяет вершину с точкой на противолежащей стороне.
Медиана треугольника, которая проводится из заданной вершины, является отрезок, соединяющий данную вершину с серединой противоположной стороны треугольника.
Средняя линия треугольника – это отрезок, который соединяет середины двух сторон данного треугольника. К этому обозначению также есть определенная теорема, которая говорит о том, что средняя линия треугольника всегда параллельна третьей стороне, а также равна ее половине.
Все эти обозначения (медиана, биссектриса, высота, средняя линия треугольника) обязательно понадобятся в решении практических задач. Скажем более того, без знания свойств этих вершин вы вряд ли сможете решить хоть какую-либо задачу, связанную с треугольниками.
Треугольники
- Решебник по математике
- Математические игры
- Справочник по математике
- Математическая литература
- Видео
- Добавить задачу
- Заказать работу
Источник: mateshka.ru