Что такое омега в физике

В курсе физики при изучении движения по окружности мы встречаем понятие угловой скорости. Обозначается греческой буквой омега ω и измеряется в радианах в секунду (рад/с). При изучении гармонических колебаний вылезает та же самая ω, только в роли циклической частоты, и с той же размерностью рад/с. Циклическая частота и угловая скорость — разные физические величины, хотя и во многом похожи. Их похожесть объясняется математическими представлением о круге.

Движение по кругу и колебания. Сходство

Рассмотрим равномерное движение точки по окружности. Если мы рассмотрим проекции этой точки на оси координат, то зависимость координат от времени будет описываться гармоническими функциями.

Движение точки по окружности. Зависимость угла от времени, и координат от времени

Если мы возьмем производную от координат по времени и посчитаем модуль скорости, то получим классическую формулу связи линейной и угловой скорости: v=Rω.

Зависимости в виде синуса и косинуса встречаются также и в задачах, связанных с гармоническими колебаниями — математический маятник, пружинный маятник, LC-контур. Только в качестве угла φ=ωt будет уже не угол поворота, а фаза колебаний. Таким образом, от представления движения по окружности, которое знакомо всем, можно переходить к анализу колебательных систем, в которых та же самая буква имеет другой физический смысл.

Что больше бесконечности?

В университетском курсе теории колебаний для анализа сложных колебательных систем используют понятие фазового портрета. Это график, по горизонтальной оси которого отложена координата, а по вертикальной — скорость. Точка на фазовом портрете — это состояние системы в некоторый момент времени.

Фазовым портретом простейшей колебательной системы — математического маятника без затухания — является окружность.

Фазовый портрет математического маятника без затухания.

В этом случае легко видеть, что угловой скоростью движения точки по фазовой плоскости будет как раз циклическая частота ω.

Итак, общность понятна, теперь перейдем к различиям.

Отличие угловой скорости и частоты

Пример 1. Математический маятник

Пусть φ — угол отклонения маятника от вертикали, тогда угловая скорость будет равна производной от угла по времени φ’.

Закон движения для математического маятника и зависимость угловой скорости от времени.

Поскольку угол меняется от времени не по линейному закону, а по гармоническому закону синуса или косинуса, то и угловая скорость будет меняться по гармоническому закону, а ее максимальное значение будет определяться амплитудой колебаний и угловой частотой: φ’ₘₐₓ=φ₀ω. Только при амплитуде колебаний, равной 1 радиану, максимальная угловая скорость по величине будет совпадать с циклической частотой. Поэтому в этом случае нельзя обозначать угловую скорость такой же буквой ω, как и циклическую частоту, нужно вводить другие обозначения.

Пример 2. Излучение

Рассмотрим электрон, движущийся по окружности с угловой скоростью ω. Согласно теории Максвелла, движущийся ускоренно электрон излучает электромагнитные волны. Будет ли частота излучения этих волн совпадать с частотой вращения электрона? Вовсе не обязательно, спектр излучения будет сложным, и зависеть от отношения скорости электрона к скорости света. При относительно малых скоростях электрона говорят о циклотронном излучении , и в его спектре действительно преобладают волны на частоте вращения, но есть и другие гармоники. Если же скорость электрона сравнима со скоростью света в вакууме, то такое излучение называют синхротронным , у него будет сплошной спектр, причем максимум не на частоте вращения, а на другой частоте, зависящей от скорости электрона.

Физика | Равномерное движение по окружности

Циклотронное и синхротронное излучение. Характерные спектры.

Итак, мы видим, что омега омеге рознь, и необходимо четко различать вращательное и колебательное движения. Конечно, примеров можно привести и больше, но на мой взгляд, это самые яркие. На этом закончу статью.

Спасибо, что дочитали до конца!

Надеюсь, что эта статья помогла прояснить непонятные моменты с омегами. А если остались вопросы — пишите в комментариях, постараюсь ответить!

Источник: dzen.ru

Угловая скорость и угловое ускорение

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
2. если задан угол поворота φ за единицу времени:
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c -1 ].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с 2 ], [с -2 ]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

• равномерное вращение (ω — const)
  
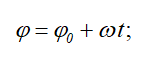
• равнопеременное вращение (ε — const)
  

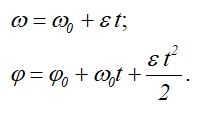
Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с 2 , r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с -1 = 9,42 рад/с.

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Источник: isopromat.ru

Чему равна омега в физике

Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).

Угловая частота является производной по времени от фазы колебания:

Другое распространённое обозначение ω = φ ˙ . >.>

Угловая частота связана с частотой ν соотношением [1]

В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:

В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2 π единиц времени.

Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC -контура равна ω L C = 1 / L C , ,> тогда как обычная резонансная частота ν L C = 1 / ( 2 π L C ) . u _ =1/(2pi ).>

В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2 π и 1/(2 π ), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.

В Викисловаре есть статья « омега »

Омега (греч. ὦ μέγα — большое «о») — последняя буква греческого алфавита. А также:

• Омега (кириллица) — буква кириллицы, а также обозначение числа 800 в кириллической системе счисления.
• Альфа и Омега (значения) — первая и последняя буквы греческого алфавита. Словосочетание, буквально означающее «начало и конец», «от и до», «от первой и до последней буквы». Часто применяется в названиях художественных произведений.

Омега в математике и информатике [ править | править код ]

• Омега-язык (ω-язык) — это множество бесконечно длинных последовательностей символов.
• Омега-код Элиаса — универсальный код для кодирования положительных целых чисел, разработанный Питером Элиасом.
• Cω (произносится: си́ оме́га, обычно записывается: Cw или Comega) — язык программирования, расширение языка программирования C#, разработанный Microsoft Research.
• Омега-мэппинг — один из способов изображения процесса общего системного мышления с помощью схем, вид диаграммы связей.

Омега в химии и физике [ править | править код ]

• Знаком Ω обозначают Ом — единицу измерения электрического сопротивления в СИ.
• Омега-3, омега-6, омега-9 — классы полиненасыщенных жирных кислот.

• Омега-гиперон (Ω − -гиперон) — элементарная частица из семейства барионов (Ω-барионы).

• ω — угловая частота.

Омега в астрономии [ править | править код ]

• Омега (ω) — обозначение звёзд в некоторых созвездиях в системе обозначений Байера буквами греческого алфавита.
• Омега — туманность в созвездии Стрельца.
• NGC 5139 — ω Центавра, шаровое скопление в созвездии Центавр.

Топонимы [ править | править код ]

• Бухта Омега — название одной из севастопольских бухт. В бухте находится одноименный пляж «Омега».

Подразделения специального назначения [ править | править код ]

• «Омега» — отряд специального назначения Управления «С» ПГУ КГБ СССР
• «Омега» — отряд специального назначения Управления ФСИН РФ Республики Хакасия, создан в 1991
• Омега (спецподразделение МВД Украины) — отряд специального назначения внутренних войск МВД Украины, создан в 2003
• «Омега» — спецподразделение Государственной службы исполнения наказаний Республики Киргизия
• «Omega» — спецподразделение полиции Латвии, создано в 1992
• «Omega» — спецподразделение МВД Грузии, создано в 1993

Музыкальные группы и произведения [ править | править код ]

• Omega (группа) — венгерская рок-группа.
• Deathspell Omega — французская блэк-метал-группа.
• Omega — альбом британской рок-группы Asia.

Автомашины [ править | править код ]

• Chevrolet Omega
• Oldsmobile Omega
• Opel Omega

«Омега» как марка технических устройств [ править | править код ]

• Омега (самолёт) — советский легкомоторный самолёт конструкции А. Н. Грацианского.
• «Омега» — прототип радиостанции «Север».
• «Омега» — радиоприёмник Р-311.
• Omega (компания) — швейцарская часовая компания, выпускающая часы под одноимённой маркой.
• Омега (компания) — российская компания по разработке и внедрению программного обеспечения для управления предприятиями, комплексной автоматизации бухгалтерского и налогового учёта средних и крупных российских предприятий.
• Omega (навигационная система) — система радионавигации.
• Омега — советская программа разработки лазерного оружия высокой мощности для ПВО.
• «Омега» — название советских космических аппаратов типа Космос-14 и Космос-23.

«Омега» в художественных произведениях, кинематографии и компьютерных играх [ править | править код ]

• Omega (Вавилон-5) — вымышленный класс космических кораблей в телесериале «Вавилон-5».
• Омега (Mass Effect) — название космической станции в виде медузы в вымышленной вселенной Mass Effect.
• Вариант «Омега» — советский пятисерийный художественный фильм, снятый в 1975 году режиссёром Антонисом-Янисом Воязосом.
• Омега Суприм (Омегатор) — персонаж-робот из мультсериала «Трансформеры».
• «Человек Омега» — американский фантастический фильм 1971 года режиссёра Бориса Сагала. Одна из экранизаций романа Ричарда Мэтисона«Я — легенда».

•Омега-персонаж из fortnite

• I Am Ωmega, букв. «Я — Омега» (Я воин) — американский художественный фильм 2007 года режиссёра Гриффa Фёрстa, экранизация романа Ричарда Мэтисона «Я — легенда».
• Омега-молекулы — один из видов оружия в вымышленной вселенной «Звёздного пути».
• Миры Омега — один из классов звёздных систем в вымышленной вселенной компьютерной игры Freelancer.
• God of War — используется символ Омега
• Омега — в дополнении SimCity Города будущего — высокотехнологичная субстанция, вызывающая зависимость. Производится корпорацией OmegaCo из нефти и железной руды.
• Омега (одиночка) — один из разрядов оборотней в телесериале «Волчонок».
• Омега Флауи — персонаж из игры Undertale.
• Е-123 Омега — персонаж из серии игр про ежа Sonic
• В American McGee’s Alice и Alice Madness Returns главная героиня, Алиса Лидделл, носит кулон в виде символа омеги
• Омега — персонаж из игры GTA V. Эксцентричный хиппи с ярко выраженными параноидальными наклонностями. Он из тех, кто верит в правительственные заговоры, инопланетян и, по всей видимости, регулярно употребляет запрещенные вещества.

Рассмотрите угловую скорость вращения тела в физике: определение, как объект вращается с угловой скоростью, формула решения задач, угловая и линейная скорость.

Чтобы проверить стремительность вращения тела, представим угловую скорость ω как скорость изменения угла:

Чем больше угол поворота за предложенный временной промежуток, тем выше угловая скорость. Единица – радиан в секунду.

Угловая скорость (ω) соответствует линейной (v). Чтобы отыскать точное соотношение между ними, рассмотрим углубление на вращающемся компакт-диске. Оно смещает длину дуги Δs за период Δt и поэтому обладает линейной скоростью v = Δs/Δt.

Из Δθ = (Δs)/r видно, что Δs = r ⋅ Δθ. Подставим в формулу для v, и видим:

v = (r ⋅ Δθ)/(Δt) = r (Δθ/Δt) = rω.

Это можно описать двумя путями: v = rω или ω = v/r.

Из первого видно, что линейная скорость (v) расположена пропорционально дистанции от центра вращения, поэтому ее максимум достигает для точки на ободе. На краю мы можем назвать ее тангенциальной скоростью.

Второе можно рассмотреть на перемещении машины. Обратите внимание на шину. Скорость точки в центре совпадает с показателями v машины. Чем быстрее движение, тем больше оборотов совершает шина, а значит v = rω. Точно также, шина большего радиуса, вращающаяся с той же угловой скоростью (ω), будет повышать линейную скорость (v).

Машина, смещающаяся вправо со скоростью v, обладает шиной с угловой скоростью ω. Скорость протектора шины относительно оси приравнивается к v так же, как если бы машину приподняли. Получается, что транспорт перемещается вперед с линейной скоростью v = rω (r – радиус шины). Большая угловая скорость шины приводит к повышению скорости автомобиля

Нет связанных сообщений

Источник: girlgames01.ru