Найдем функцию распределения длин свободного пробега молекул. Обозначим через вероятность того, что молекула пролетит расстояние l без столкновений. Тогда вероятность того, что молекула пролетит расстояние без столкновений, будет равна произведению вероятностей двух независимых событий: события, что молекула пролетит расстояние l без столкновений и события, что молекула пролетит расстояние без столкновений, т. е.
Вероятность же соударения на пути dl, очевидно, пропорциональна dl
где – коэффициент пропорциональности.
Вероятность же, что молекула пройдет расстояние без столкновения, очевидно, равна:
Подставим (4.2.3) в (4.2.1). В результате будем иметь
С другой стороны, разлагая функцию в ряд по степеням в точке l, получим:
Из сравнения выражений (4.2.4 – 4.2.5), будем иметь:
Проинтегрируем последнее уравнение.
где lnb – произвольная постоянная. Из последнего соотношения находим
Вероятность того, что молекула на расстоянии l испытывает столкновение, очевидно, равна
Физическая кинетика. Часть 1. Длина свободного пробега. Эффективный диаметр.
Функция , таким образом, представляет собой интегральную функцию распределения длин свободного пробега молекул. Для нахождения плотности вероятности необходимо продифференцировать (4.2.9) по переменной l (см. формулу (А. 20) прил. А):
Чтобы определить две произвольные постоянные, необходимо располагать двумя уравнениями. Первое из них – это условие нормировки для плотности вероятности w(l):
Второе уравнение – это выражение для средней длины свободного пробега:
Подставляя выражение (4.2.10) в (4.2.11), получим, что b = 1. Подставляя w(l) из (4.2.10) в (4.2.12) и интегрируя по частям, получим, что .
Таким образом, функция распределения длин свободного пробега молекул (формула Клаузиуса) примет вид:
4.3. Рассеяние молекулярного пучка в газе. Экспериментальное определение средней длины свободного пробега
Предположим, что узкий пучок, состоящий из N0 молекул, движется через газ в направлении оси X. Примем условие, что каждая частица пучка, сталкиваясь с молекулами газа, выбывает из пучка. Пусть в произвольный момент времени начала наблюдения в пучке было N молекул. Пройдя расстояние dx, молекулы пучка испытают Ndx/ < λ >столкновений и выбудут из пучка. Поэтому
Перепишем последнее соотношение в виде:
Проинтегрируем левую часть равенства (4.3.3) в пределах от N0 до N, а правую – от 0 до x:
После интегрирования получим
Таким образом, ослабление молекулярного пучка в газе происходит по экспоненциальному закону.
Формула (4.3.5) используется при экспериментальном определении средней длины свободного пробега молекул. Опыт М. Борна ставится следующим образом (рис. 59).
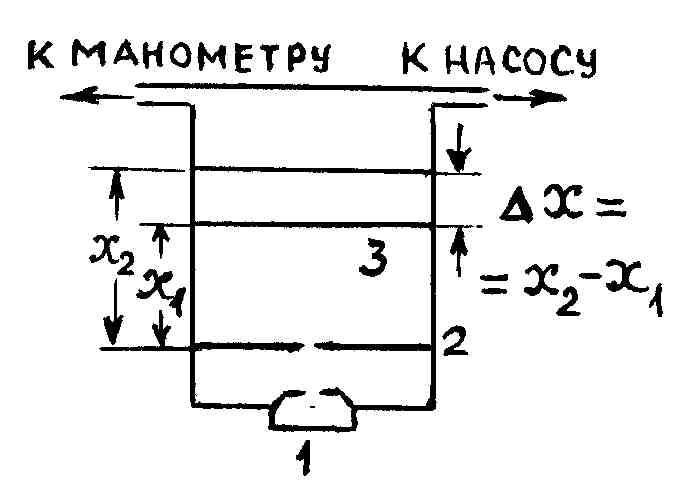
В сосуде, наполненном воздухом, имеются: источник 1 (печь), создающий поток атомов серебра, который, проходя систему диафрагм 2 с малыми отверстиями, превращается в узкий пучок, и стеклянной пластинки 3, на которой осаждалось серебро. Количество осадка пропорционально числу N атомов, падающих на пластинку 3. В сосуде с помощью насоса можно создавать любые заданные давления.
Длина свободного пробега
Сначала на одной из пластинок, находящейся на расстоянии x1 от отверстия диафрагмы, в течение определенного промежутка времени осаждалось серебро. Затем осаждалось серебро на другой пластинке, расположенной на расстоянии x2, в течение того же промежутка времени. Измеряя отношение N2/N1 по плотности осадка серебра на пластинках, нетрудно, используя формулу (4.3.5), определить среднюю длину свободного пробега атомов серебра
Измерения величины , проведенные при различных давлениях и температурах, показали удовлетворительное согласие опытных данных с соответствующими расчетами, проведенными по формуле (4.1.10).
Источник: studfile.net
Длина свободного пробега молекулы
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Длина свободного пробега молекулы — среднее расстояние, которое частица пролетает за время свободного пробега от одного столкновения до следующего.
![]()
Длина свободного пробега каждой молекулы различна, поэтому в кинетической теории вводится понятие средней длины свободного пробега l. Величина l является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры
Если нам нужно выразить формулу через давление и температуру, то производим маленькую замену в 1 части формулы:
![]()
Заменяем количество вещества на полученную нами формулу, и у нас получается:
![]()
![]() , , , значение средней длины свободного пробега будет:
, , , значение средней длины свободного пробега будет:
![]()
В Формуле мы использовали :
![]() — Длина свободного пробега молекулы
— Длина свободного пробега молекулы
— Эффективный диаметр молекулы
— Концентрация молекул
— Давление
![]() — Постоянная Больцмана
— Постоянная Больцмана
— Температура, при которой находится газ
Источник: xn--b1agsdjmeuf9e.xn--p1ai
Средняя длина свободного пробега электронов
Можно оценить среднюю длину свободного пробега электронов в твердом теле, содержащем п электронов в единице объема, в рамках общей теории потерь энергии в твердых телах:

где В — отношение энергии частицы к энергии возбуждения. Преобладающая часть потерь энергии электронов в твердом теле приходится на возбуждение плазмонов посредством дальних столкновений. Потери энергии происходят дискретными порциями, равными величине кванта htop. Таким образом, можно положить

и переписать (5.20) в виде
Если плазмоны — главная причина потерь энергии при определении средней длины свободного пробега электронов Я, то можно записать

откуда
Например, вычисленное по формуле (5.24) значение Я в алюминии равно 9,2 А для электронов с энергией 350 эВ (hv = 15 эВ, и 2 = 2Е/т = 1,23• 10 18 ). Полученное значение хорошо согласуется с данными, приведенными на рис. 5.5.
Оже-процесс и процесс эмиссии рентгеновского кванта
В спектре вторичных электронов (разд. 3.2.1, рис. 3.1) есть группы электронов, энергия которых не зависит от энергии первичных электронов, а определяется атомами, испустившими эти электроны. Это — оже- электроны, являющиеся основой широко известного метода — электронной оже-спектроскопии (ЭОС). На рис.
5.6 приведена обобщенная диаграмма уровней энергии электронов в твердом теле, включающая уровни остовиых атомов и зонную структуру обобществленных валентных электронов. С помощью данной диаграммы образование оже- элекгронов и рентгеновских квантов можно пояснить следующим образом.

Рис. 5.6. Диаграмма уровней энергии электронов в твердом теле и схемы оже-процесса и образования рентгеновского кванта
Первичный электрон с энергией Ер создает вакансию на глубоком уровне К остовного атома. Образовавшаяся вакансия через время t ~ 10 _14 -10 |6 с заполняется электроном с какого-либо верхнего уровня (в приведенном на рис. 5.6 примере с уровня L).
Избыток энергии Ек ~ Ец может освободиться одним из двух путей: 1) излучения рентгеновского кванта с энергией Рио =ЕК-Е1Л (волнистая линия внизу рисунка); 2) оже-процесса (стрелки между уровнями Ьх—*К и Ь2 -^?вверх). Первый процесс более вероятен при энергии связи электрона, превышающей 1 кэВ, второй — для легких атомов и энергии связи электрона, не превышающей 1 кэВ. В случае оже-процесса избыточная энергия передастся третьему электрону, находящемуся, например, на уровне Ь2. В результате в вакуум испускается оже-электрон с энергией

Слагаемое U в формуле учитывает, что в конечном состоянии атом оказывается дважды ионизованным в результате образования вакансий на уровнях Ь и Ь2. Он учитывает увеличение энергии связи ?2-электрона, когда удален 7,гэлектрон, и ?гэлектрона при наличии вакансии на уровне Ь2. Для вычисления слагаемого U(L,L2) используют эмпирическое соотношение, достаточно хорошо согласующееся с экспериментальными результатами:

где Z — атомный номер элемента.
Формулы (5.25) и (5.26) можно обобщить в виде

где — энергия оже-перехода а/2у элемента Z. Первые три члена в
(5.27) соответствуют разности энергий связи оболочек а, /2 и у элемента с атомным номером Z. Поправочный член мал и включает среднее от возрастания энергии связи у-электрона, когда /2-элсктрон удален, и /2-электрона, когда у-электрон удален. Измеренные величины оже- переходов наряду с величинами энергий связи табулированы. Численная проверка приближения, отраженного формулой (5.27), для переходов KLL выявляет хорошее согласие между теорией и экспериментом.
На рис. 5.7 показан оже-переход в атоме, который, по понятным из рисунка причинам, обозначают KLL2. Если в ожс-процсссе задействованы электроны валентной зоны, оже-процесс обозначается, например, так L22 VV2 (или LVV), где V, и V2 расположены в областях максимума плотности состояний валентной зоны. Конечное состояние обычно описывается с использованием спектроскопических обозначений для орбиталей. Например, переход KLL оставляет пустой оболочку 2s (две вакансии) и оболочку 2р с шестью электронами; переход обозначается как KLL (2s a 2p e ). Переход KL2 L2 оставляет вакансии в оболочке 2р и обозначается как KL2 L2 (2s’2p 4 ). Даже при сравнительно простом переходе KLL существует большое разнообразие конечных состояний, которые могут иметь слегка различающиеся энергии и поэтому отвечать слегка различающимся оже-линиям.
Процесс эмиссии рентгеновского кванта более подробно рассмотрен в разделе 5.8.
Источник: studme.org