Есть только 1 способ это проверить

9 способов узнать всё про человека, имея только его имя и фамилию

Многие люди недооценивают, как много информации можно найти о них в интернете, зная только их имя и фамилию.

И ведь любой желающий имеет доступ к этим данным! Потому что все сервисы, о которых речь пойдет ниже, бесплатные и легальные.

Расскажу о самых простых способах узнать всё о человеке по ФИО.

1. Находим человека в соцсетях

Первым делом по имени и фамилии можно найти человека во всех популярных социальных сетях, конечно, если он там зарегистрирован.

Советую начать с ВКонтакте, поскольку в России это самая популярная соцсеть, к тому же у неё есть хорошие фильтры для поиска.

▶️ Верни меня 1 и 2 серия — Мелодрама | Фильмы и сериалы — Русские мелодрамы

Затем можно искать человека в Instagram, Facebook, Одноклассниках и Twitter.

Не забывайте, что имя в интернете может не совпадать с данными паспорта. И если фамилию, как правило, пользователи редко меняют, то вместо Евгения человек может подписаться Женя. Поэтому учитывайте этот нюанс.

И еще один совет: когда найдете профиль в одной соцсети, пробейте имя пользователя в других сервисах. Вполне возможно, что человек везде использует одинаковый ник.

2. Как узнать, каким бизнесом владеет человек

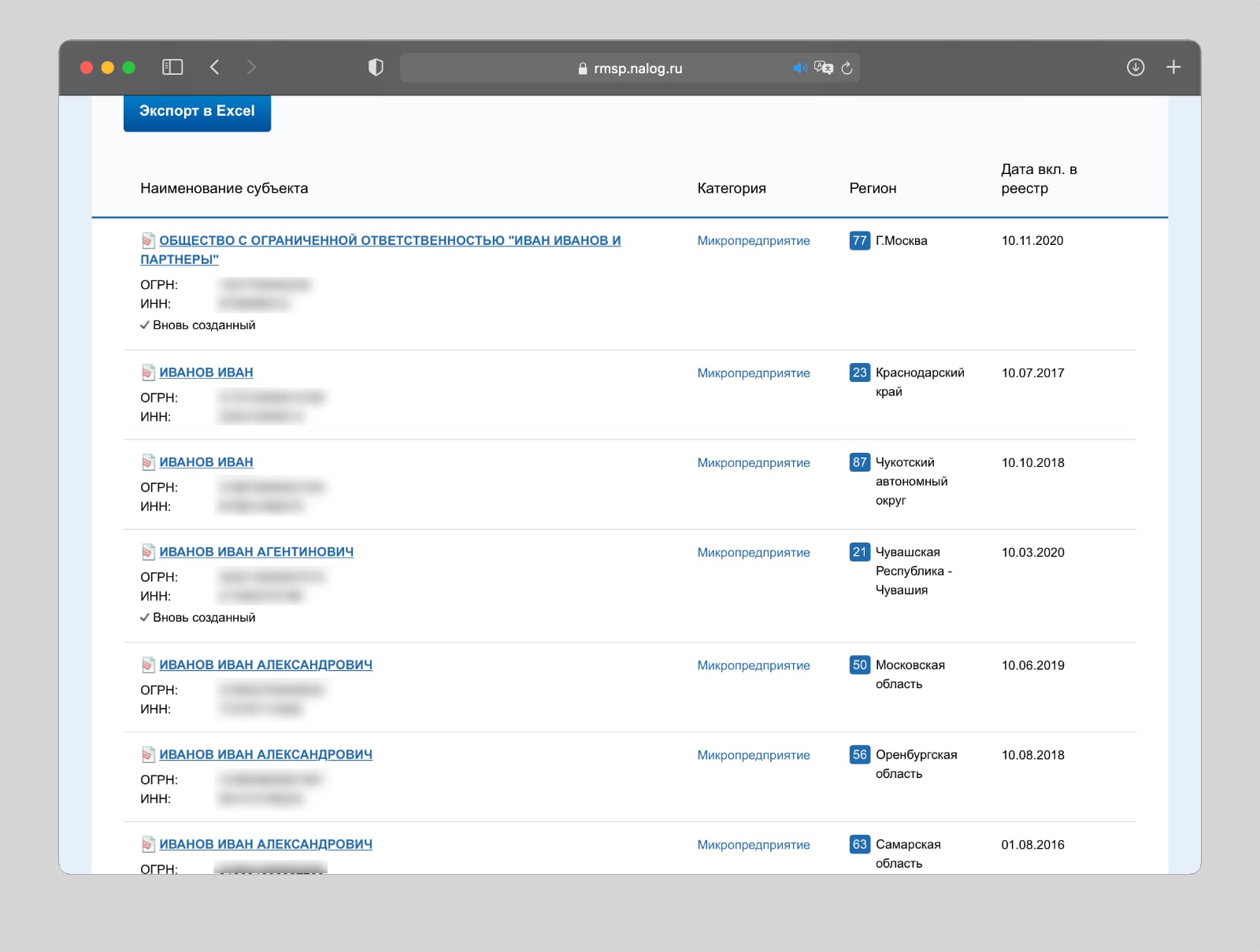
На сайте налоговой есть сервис по поиску предпринимателей по имени и фамилии. С помощью этой информации мы можем узнать, чем примерно занимается человек.

Кроме того, в базе открыто хранится номер ИНН. Первые его четыре цифры являются кодом подразделения ФНС. Ищем его в Google или Яндексе, и выясняем, в каком городе человек зарегистрировал ИП. Зная родной город незнакомца, искать его будет намного проще.

3. Что можно найти в Google и Яндексе

Поисковые системы могут выдать интересные результаты. Например, сайты и форумы, на которых зарегистрирован человек.

Таким образом, можно найти место работы, учебы и даже упоминания в СМИ. Правда для последнего потребуется чуть больше информации.

4. Как узнать, находится ли человек в розыске

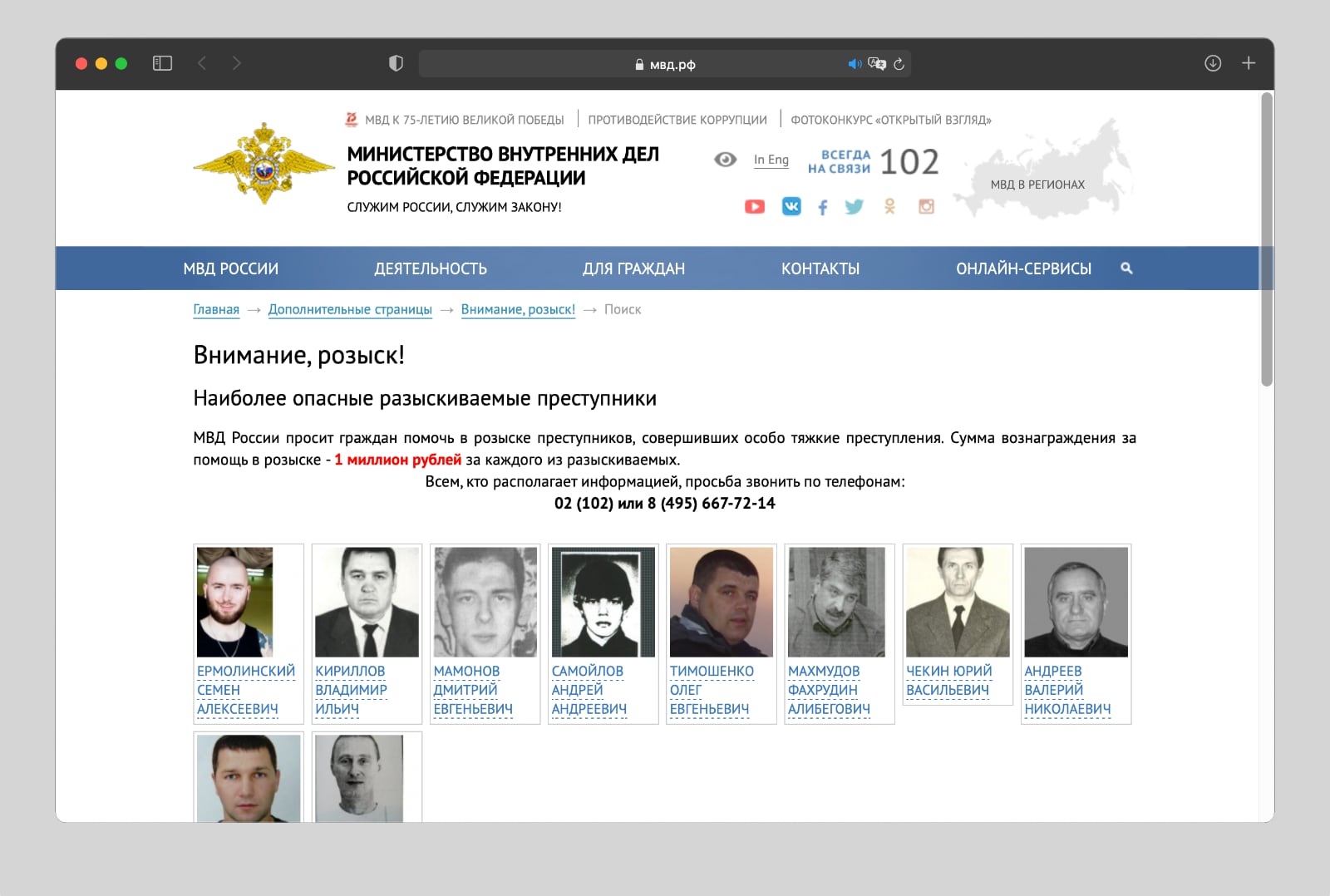
На всякий случай человека можно попробовать найти в базе МВД, особенно, если он вызывает опасения.

У МВД есть для этого бесплатный сервис, только для поиска придется указать год рождения. Данное поле можно заполнить наугад, если знаете примерный возраст.

Мобилизация в России! Законный способ избежать мобилизации

5. Как проверить долги человека

На главной странице сайта Федеральной службы судебных приставов есть поиск задолженностей, в том числе штрафов и алиментов.

Можно указать номер исполнительного производства или ФИО, причем отчество необязательное поле. В общем, пишем имя и фамилию, а затем изучаем базу.

6. Какие научные публикации есть у незнакомца

C помощью сервиса Google Академия можно найти научные статьи, которые опубликовал человек. В отличие от обычного Google Поиска, Академия ищет публикации и в закрытых библиотеках.

Для использования этого сервиса не помешает информация о месте учебы или работы. Это иногда указывается в Facebook и ВКонтакте.

7. Как найти неизвестного человека в судебных базах

На сайте государственной системы Правосудие можно проверить, в каких судебных делах участвовал незнакомец. Для этого понадобится только имя и фамилия, но лучше знать как можно больше данных, чтобы получить наиболее релевантные результаты поиска.

К сожалению, не ко всем делам прикреплен текст решения судьи. Но если он будет, то сможете прочитать почти все детали процесса (некоторая конфиденциальная информация в документах не указывается).

8. Как узнать, жив ли человек или нет

Если вы почти ничего не знаете про человека которого ищете, то не помешает проверить, живой ли он или уже умер.

Для этого можно воспользоваться справочной Федеральной нотариальной палаты.

9. Как найти информацию в архивах

Если вы ищете неживого человека, то все сервисы в этой статье будут бесполезны. Зато в FamilySpace можно найти старые архивы, в которых упоминается незнакомец.

В FamilySpace хранятся материалы переписей населения, метрические книги, адресные книги городских жителей, списки победителей и многое другое.

Что я нашел о себе в интернете

Я решил проверить некоторые из этих способов на себе. Первым делом написал свое имя в Google и нашел аккаунты в Twitter и Facebook. Затем открыл Яндекс и на первой странице увидел свой профиль в Instagram.

Больше всего я удивился, что мне не удалось найти страницу во ВКонтакте.

Однако мое имя пользователя в Facebook совпадает с ВКонтакте, поэтому я без проблем нашел аккаунт с помощью Google.

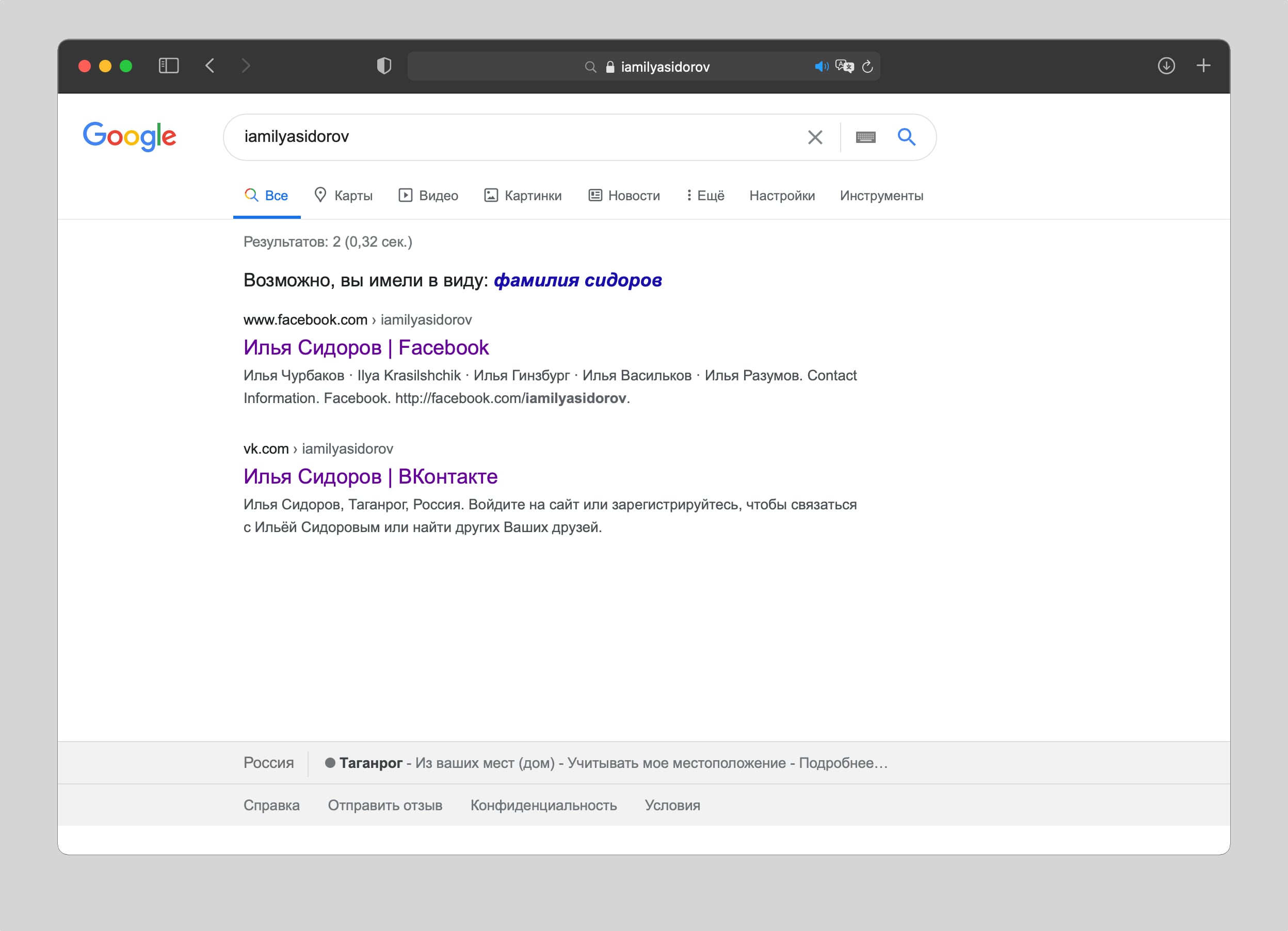
Помимо страниц в соцсетях, я нашел ссылки на свои материалы на iPhones.ru и других сайтах, где я работал раньше.

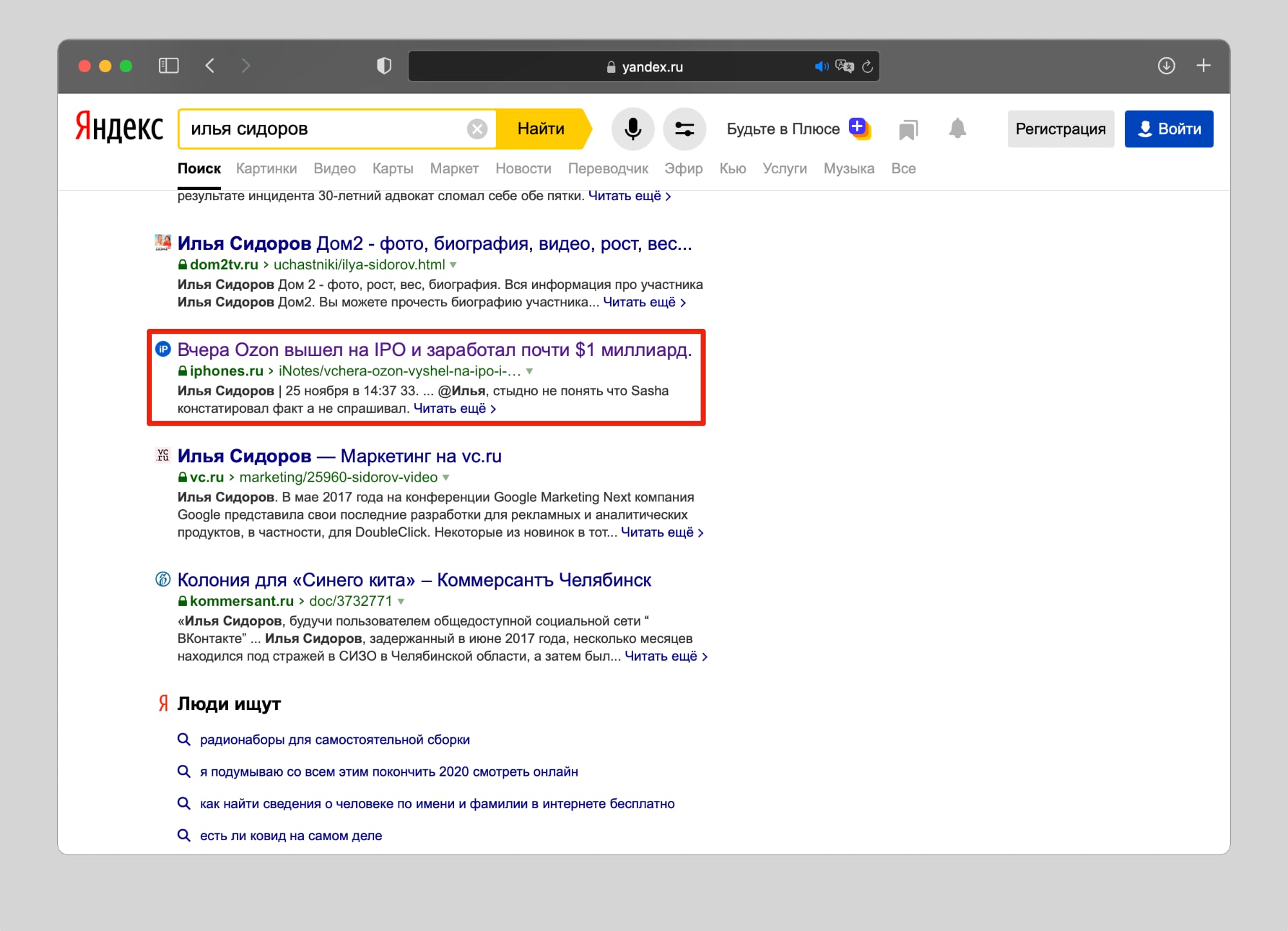
Благодаря Яндекс.Картинкам у меня получилось найти фото профиля на YouTube, а вместе с ним ссылку на свой канал.

В реестре предпринимателей я не стал искать себя, поскольку никогда не открывал ИП и ООО.

В базах МВД, ФССП и Правосудия про меня ничего нет.

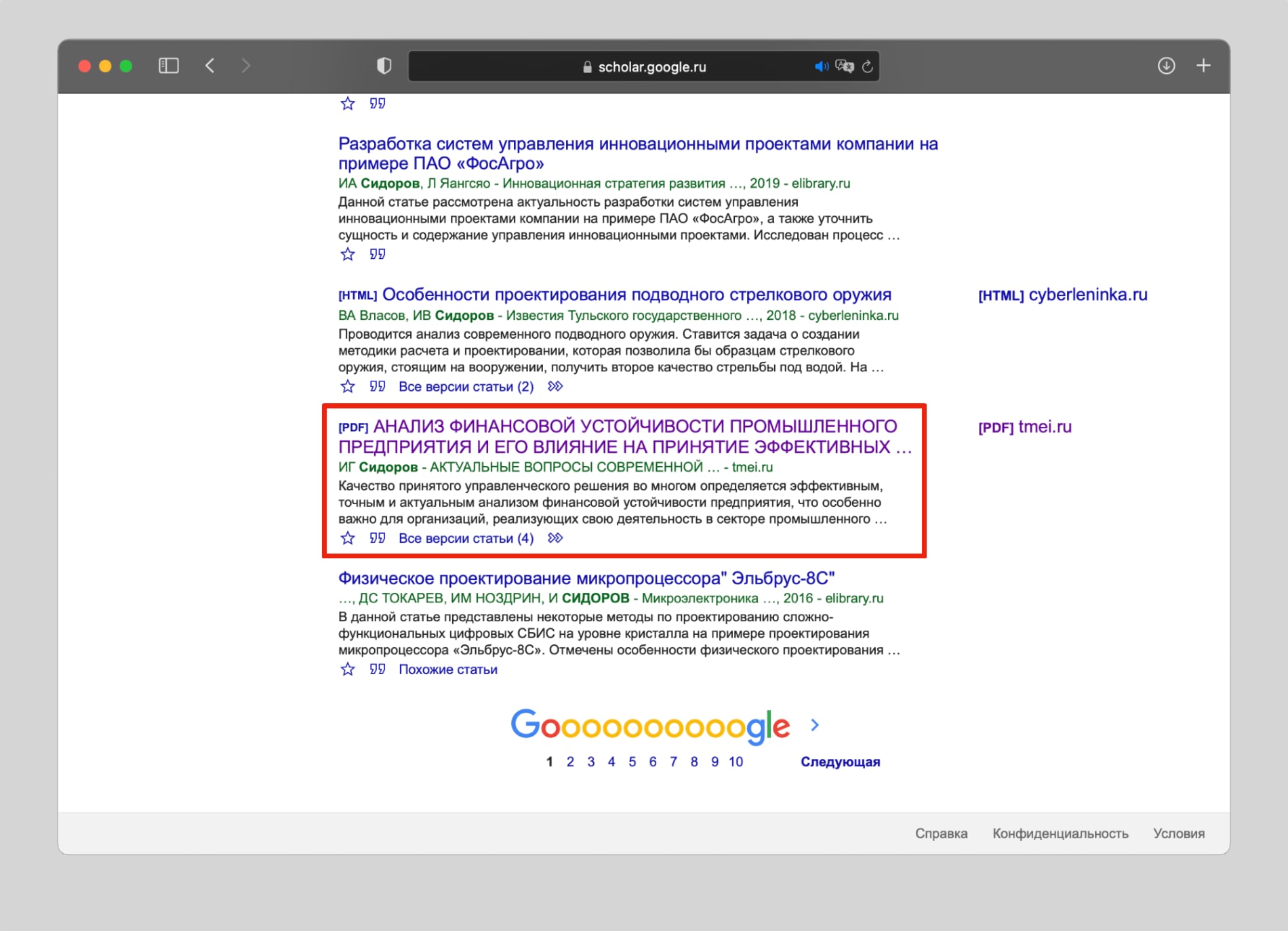
С помощью Google Академии нашел ссылку на свой доклад на научную конференцию, которая проходила в моем институте.

В итоге, зная только имя и фамилию, у меня получилось найти страницы в социальных сетях, место учебы, работы, научные публикации и фотографии.

Если проанализировать соцсети и попытаться найти другие фото, то можно получить еще больше информации.

Источник

Алгоритмы поиска простых чисел

«Самое большое простое число 2 32582657 -1. И я с гордостью утверждаю, что запомнил все его цифры… в двоичной форме».
Карл Померанс

Натуральное число называется простым, если оно имеет только два различных делителя: единицу и само себя. Задача поиска простых чисел не дает покоя математикам уже очень давно. Долгое время прямого практического применения эта проблема не имела, но все изменилось с появлением криптографии с открытым ключом. В этой заметке рассматривается несколько способов поиска простых чисел, как представляющих исключительно академический интерес, так и применяемых сегодня в криптографии.

Решето Эратосфена

Решето Эратосфена — алгоритм, предложенный древнегреческим математиком Эратосфеном. Этот метод позволяет найти все простые числа меньше заданного числа n. Суть метода заключается в следующем. Возьмем набор чисел от 2 до n.

Вычеркнем из набора (отсеим) все числа делящиеся на 2, кроме 2. Перейдем к следующему «не отсеянному» числу — 3, снова вычеркиваем все что делится на 3. Переходим к следующему оставшемуся числу — 5 и так далее до тех пор пока мы не дойдем до n. После выполнения вышеописанных действий, в изначальном списке останутся только простые числа.

Алгоритм можно несколько оптимизировать. Так как один из делителей составного числа n обязательно , алгоритм можно останавливать, после вычеркивания чисел делящихся на .

Иллюстрация работы алгоритма из Википедии:

Сложность алгоритма составляет , при этом, для хранения информации о том, какие числа были вычеркнуты требуется памяти.

Существует ряд оптимизаций, позволяющих снизить эти показатели. Прием под названием wheel factorization состоит в том, чтобы включать в изначальный список только числа взаимно простые с несколькими первыми простыми числами (например меньше 30). В теории предлагается брать первые простые примерно до . Это позволяет снизить сложность алгоритма в раз. Помимо этого для уменьшения потребляемой памяти используется так называемое сегментирование. Изначальный набор чисел делится на сегменты размером и для каждого сегмента решето Эратосфена применяется по отдельности. Потребление памяти снижается до .

Решето Аткина

Более совершенный алгоритм отсеивания составных чисел был предложен Аткином и Берштайном и получил название Решето Аткина. Этот способ основан на следующих трех свойствах простых чисел.

Если n — положительное число, не кратное квадрату простого числа и такое, что . То n — простое, тогда и только тогда, когда число корней уравнения нечетно.

Если n — положительное число, не кратное квадрату простого числа и такое, что . То n — простое, тогда и только тогда, когда число корней уравнения нечетно.

Если n — положительное число, не кратное квадрату простого числа и такое, что . То n — простое, тогда и только тогда, когда число корней уравнения нечетно.

Доказательства этих свойств приводятся в этой статье.

На начальном этапе алгоритма решето Аткина представляет собой массив A размером n, заполненный нулями. Для определения простых чисел перебираются все . Для каждой такой пары вычисляется , , и значение элементов массива , , увеличивается на единицу. В конце работы алгоритма индексы всех элементов массива, которые имеют нечетные значения либо простые числа, либо квадраты простого числа. На последнем шаге алгоритма производится вычеркивание квадратов оставшихся в наборе чисел.

Из описания алгоритма следует, что вычислительная сложность решета Аткина и потребление памяти составляют . При использовании wheel factorization и сегментирования оценка сложности алгоритма снижается до , а потребление памяти до .

Числа Мерсенна и тест Люка-Лемера

Конечно при таких показателях сложности, даже оптимизированное решето Аткина невозможно использовать для поиска по-настоящему больших простых чисел. К счастью, существуют быстрые тесты, позволяющие проверить является ли заданное число простым. В отличие от алгоритмов решета, такие тесты не предназначены для поиска всех простых чисел, они лишь способны сказать с некоторой вероятностью, является ли определенное число простым.

Один из таких методов проверки — тест Люка-Лемера. Это детерминированный и безусловный тест простоты. Это означает, что прохождение теста гарантирует простоту числа. К сожалению, тест предназначен только для чисел особого вида , где p — натуральное число. Такие числа называются числами Мерсенна.

Тест Люка-Лемера утверждает, что число Мерсенна простое тогда и только тогда, когда p — простое и делит нацело -й член последовательности задаваемой рекуррентно: для .

Для числа длиной p бит вычислительная сложность алгоритма составляет .

Благодаря простоте и детерминированности теста, самые большие известные простые числа — числа Мерсенна. Самое большое известное простое число на сегодня — , его десятичная запись состоит из 24,862,048 цифр. Полюбоваться на эту красоту можно здесь.

Теорема Ферма и тест Миллера-Рабина

Простых чисел Мерсенна известно не очень много, поэтому для криптографии с открытым ключом необходим другой способ поиска простых чисел. Одним из таким способов является тест простоты Ферма. Он основан на малой теореме Ферма, которая гласит, что если n — простое число, то для любого a, которое не делится на n, выполняется равенство . Доказательство теоремы можно найти на Википедии.

Тест простоты Ферма — вероятностный тест, который заключается в переборе нескольких значений a, если хотя бы для одного из них выполняется неравенство , то число n — составное. В противном случае, n — вероятно простое. Чем больше значений a использовано в тесте, тем выше вероятность того, что n — простое.

К сожалению, существуют такие составные числа n, для которых сравнение выполняется для всех a взаимно простых с n. Такие числа называются числам Кармайкла. Составные числа, которые успешно проходят тест Ферма, называются псевдопростыми Ферма. Количество псевдопростых Ферма бесконечно, поэтому тест Ферма — не самый надежный способ определения простых чисел.

Тест Миллера-Рабина

Более надежных результатов можно добиться комбинируя малую теорему Ферма и тот факт, что для простого числа p не существует других корней уравнения , кроме 1 и -1. Тест Миллера-Рабина перебирает несколько значений a и проверяет выполнение следующих условий.

Пусть p — простое число и , тогда для любого a справедливо хотя бы одно из условий:

1. Существует целое число r < sтакое, что

Чем больше свидетелей простоты найдено, тем выше вероятность того, что n — простое. Согласно теореме Рабина вероятность того, что случайно выбранное число a окажется свидетелем простоты составного числа составляет приблизительно .

Следовательно, если проверить k случайных чисел a, то вероятность принять составное число за простое .

Сложность работы алгоритма , где k — количество проверок.

Благодаря быстроте и высокой точности тест Миллера-Рабина широко используется при поиске простых чисел. Многие современные криптографические библиотеки при проверке больших чисел на простоту используют только этот тест и, как показал Мартин Альбрехт в своей работе , этого не всегда оказывается достаточно.

Он смог сгенерировать такие составные числа, которые успершно прошли тест на простоту в библиотеках OpenSSL, CryptLib, JavaScript Big Number и многих других.

Тест Люка и Тест Baillie–PSW

Чтобы избежать уязвимости, связанные с ситуациями, когда сгенерированное злоумышленником составное число, выдается за простое, Мартин Альбрехт предлагает использовать тест Baillie–PSW. Несмотря на то, что тест Baillie–PSW является вероятностным, на сегодняшний день не найдено ни одно составное число, которое успешно проходит этот тест. За нахождение подобного числа в 1980 году авторы алгоритма пообещали вознаграждение в размере $30. Приз пока так и не был востребован.

Ряд исследователей проверили все числа до и не обнаружили ни одного составного числа, прошедшего тест Baillie–PSW. Поэтому, для чисел меньше тест считается детерминированным.

Суть теста сводится к последовательной проверке числа на простоу двумя различными методами. Один из этих методов уже описанный выше тест Миллера-Рабина. Второй — тест Люка на сильную псевдопростоту.

Тест Люка на сильную псевдопростоту

Последовательности Люка — пары рекуррентных последовательностей , описываемые выражениями:

Пусть и — последовательности Люка, где целые числа P и Q удовлетворяют условию

Найдем такие r, s для которых выполняется равенство

Для простого числа n выполняется одно из следующих условий:

1. n делит
2. n делит для некоторого j < r

Вероятность того, что составное число n успешно пройдет тест Люка для заданной пары параметров P, Q не превышает 4/15. Следовательно, после применения теста k раз, эта вероятность составляет .

Тесты Миллера-Рабина и Люка производят не пересекающиеся множества псевдопростых чисел, соответственно если число p прошло оба теста, оно простое. Именно на этом свойстве основывается тест Baillie–PSW.

В зависимости от поставленной задачи, могут использоваться различные методы поиска простых чисел. К примеру, при поиске больших простых чисел Мерсенна, сперва, при помощи решета Эратосфена или Аткина определяется список простых чисел до некоторой границы, предположим, до . Затем для каждого числа p из списка, с помощью теста Люка-Лемера, на простоту проверяется .

Чтобы сгенерировать большое простое число в криптографических целях, выбирается случайное число a и проверяется тестом Миллера-Рабина или более надежным Baillie–PSW. Согласно теореме о распределении простых чисел, у случайно выбранного числа от 1 до n шанс оказаться простым примерно равен . Следовательно, чтобы найти простое число размером 1024 бита, достаточно перебрать около тысячи вариантов.

Источник