Как будет вести себя пучок атомов серебра попадая в неоднородное магнитное поле

Ложь на лжи сидит и ложью погоняет.
Народная поговорка.

В 1921 году двое немецких учёных Штерн и Герлах провели серию опытов с пропусканием узкого пучка атомов серебра через сильно неоднородное магнитное поле. При выключенном магните на пластинке за магнитом появлялась одна зеркальнaя полоска осевшего серебра. При включённом – две симметрично расположенных относительно центральной.
Объяснение опыту пришло в 1925 году, когда двое голландских физиков Гаудсмит и Юленбек опубликовали статью о неком предположительном вращении электрона вокруг собственной оси (спин) и создаваемом этим вращением собственным магнитным моментом электрона, позднее получившем название Магнетон Бора, хотя сам Бор вначале эту идею полностью отверг.
Я уже писал не раз, что во всех учебниках по квантовой механике в главе, посвящённой спину, немедленно появляется категорическая оговорка, что, де, никакого в обычном смысле вращения электрона вокруг своей оси нет и не может быть потому что не может быть никогда. Причём, опираясь на ссылку в чисто «классических» представлениях об электроне как неком упругом заряженном вращающемся шарике. Если это явление «сугубо квантовое», то и объясняйте его с позиций сугубо квантовых.

ЧК_МИФ_3_2_5_2_(L3) ОПЫТ ШТЕРНА-ГЕРЛАХА

ОБЪЯСНЕНИЯ НЕ ТОЛЬКО НЕ ДАЁТСЯ, но и даже вроде как запрещается. Мол, есть нечто и его же нет вовсе! Нечто, объяснению принципиально НЕ ПОДДАЮЩЕЕСЯ,
И так вся квантовая теория!

Но при чём здесь опыт Штерна-Герлаха.
А вот при чём: Де, атомы серебра собственного магнитного момента в так называемом «основном состоянии», невозбуждённом никакими внешними причинами, НЕ ИМЕЮТ. Единственное , что имеет магнитный момент, это электроны, спиново вращающиеся, которого, (вращения) на самом деле вовсе и нет!
Эти магнитные моменты электронов превращают атомы серебра в микромагнитики. Попав в сильно неоднородное магнитное поле эти магнитики (ранее хаотически направленные) не только поворачиваются этим полем, но и сдвигаются в одну или другую сторону в зависимости от направления поля магнитиков. Поэтому пучок расщепляется на два узких пучка (из-за специальных щелей при вылете из испарителя). Одни спины и магнитные моменты электронов поворачиваются по полю, а другие против поля, вот и разделяются они неоднородным магнитным полем.
И физики торжественно назвали это Пространственным Квантованием. При чём здесь пространство и почему квантование?
А это выглядит по-загадочней и более наукообразно. Ведь, если сказать, что электроны-микромагнитики ориентируются во внешнем магнитном поле – это же слишком заурядно и ПОНЯТНО, а надо – ПО-НЕПОНЯТНЕЙ!
Стрелки компасов ведь тоже ориентируются, так это ещё древним китайцам было известно, а, вот, ПРОСТРАНСТВЕННОЕ КВАНТОВАНИЕ ни им, и НИКОМУ до квантовиков в голову не приходило.
И что же происходит?
Оказывается, атомы с этими микромагнитиками -электронами поворачиваются. Одни вдоль поля, другие, в том же количестве, против поля. Вот и расходятся!

Квантовая механика 2 — Эксперимент Штерна-Герлаха. Спин электрона.

А теперь попробуем честно, без жульничества и наукоподобных Пространственных Квантований» разобраться в этом опыте и понять ЧТО к ЧЕМУ.

Представьте себе, что у вас есть много крупных свинцовых дробинок. Давайте-ка просверлим во всех тоненькие дырочки-канальцы и вставим в них тоненькие стержневые магнитики. Окрасим наши дробинки в синий цвет у северного полюса и в красный – у южного.

Будем теперь бросать эти дробинки через щель магнита тоже с очень неоднородным полем, но так, чтобы дробинки не прилипали к магниту, а быстро пролетали между его полюсами. И падали на некую клейкую пластину. Что мы увидим? Что ВСЕ дробинки отклонятся чуть от вертикали и упадут на клейкую пластину слегка «сбоку» от вертикали. ТОЛЬКО С ОДНОЙ СТОРОНЫ, И ВСЕ дробинки будут повёрнуты одной синей или красной стороной в одну сторону.
Почему все повернутся в одну сторону?
Да, потому, что магнитное поле при пролёте через щель повернёт их так же, как земное магнитное поле поворачивет все стрелки компасов.
А почему не разделит на два потока?
Потому что мощное магнитное поле «не умеет» поворачивать магнитики стрелки иначе. Тогда были у нас бы два вида компасов: Одни синей стрелкой указывают на север, другие на юг.
Но магнитное поле Земли об этих гениальных задумках физиков-квантовиков НЕ ЗНАЕТ и поэтому ВСЕ магниты ВСЕГДА поворачивает в одну сторону.
А почему они сместятся чуть вбок от вертикали?
Потому что неоднородное поле, именно, не только поворачивает, но ещё и смещает в сторону движущиеся сквозь него магниты.

Спины электронов и их магнитные моменты могут поворачиваться, но никак НЕ ПРОТИВ ПОЛЯ! Ибо нет никаких ограничивающих их ориентацию сил.
Уже поэтому, такое ОБЩЕПРИНЯТОЕ в квантовой механике объяснение есть наглая и неприкрытая ЛОЖЬ!
Магнитные моменты электронов МОГУТ поворачиваться под действием внешнего поля куда угодно, но только ПО ПОЛЮ!
И НИКОГДА САМИ СОБОЙ НЕ ПОВЕРНУТСЯ ПРОТИВ ПОЛЯ!

Но опыт даёт нам нечто другое!
Почему?
В природе все вещества физики условно разделили по их магнитным свойствам на три класса: Парамагнитики, Диамагнетики и Ферромагнетики
Парамагнетики – это вещества, у которых, под действием внешнего магнитного поля появляется своё слабое поле той же направленности.
Диамагнетики – это вещества, у которых при тех же условиях своё слабое магнитное поле повёрнуто ПРОТИВ внешнего.
Ферромагнетики – железоподобные, железо, кобальт и никель и различные специальные сплавы, это вещества, в которых под действием внешнего магнитного поля появляется своё , очень мощное поле, той же направленности, что и внешнее.
(Об антиферромагнетиках я говорить не буду, чтобы не задуривать читателям голову ненужными деталями).

Серебро является ДИАМАГНЕТИКОМ.
Его атомы обладают некосй способностью из-за так называемой Ларморовской прецессии орбит создавать противонаправленное внешнему магнитное поле.
Так, что происходит в опыте?
Скорей всего следующее.
Атомы серебра, сохраняющие природный диамагнетизм, отклоняются в одну сторону. Но есть атомы серебра, которые в мощном поле магнита становятся парамагнетиками, и поэтому они отклоняются в другую сторону. Говорить, что атомы остаются в прежнем невозбуждённом состоянии в мощном и неоднородном поле, это высказывать некую аксиому, ничем не доказанную и не подтверждённую.
Эффект Зеемана с расщеплением спектральных линий атомов в мощном магнитном поле как раз указывает на то, что энергетические орбитали электронов претерпевают изменения! Поэтому наше предположение, что часть атомов серебра остаётся диамагнетиками, а другая, под действием поля магнита (скажем, двигавшиеся очень близко к острому выступу магнита) превращается в парамагнетики, вполне резонно.
Во всяком случае, это больше соответствует явлениям природы, где свободно ориентирующиеся магниты ещё никогда не поворачивались ПРОТИВ ПОЛЯ, как этого очень хотят физики-квантовики! И своей нелепой байкой пудрят мозги дуракам-неофитам, вбивая в них серии невыдёргиваемых гвоздей – ложных догм.
Главное орудие труда в науке – это ГВОЗДЕДЁР!!
17 I 2022

P.S. Ещё мыслишки, пришедшие в голову с опозданием в несколько часов.
Тугодум-с!
Кроме упомянутого «кинематического эффекта Зеемана», отличного от общеизвестного «оптического», с расщеплением спектральных линий, результат опыта мог быть связан и с другими эффектами.

Другое предположение связано с тем, что атомарное серебро могло быть химически несравненно более активным, чем обычное молекулярное. (Вспомним химическую активность атомарного водорода или кислорода!). Из-за этого серебро могло вступать в химическую реакцию с атомами азота и кислорода, которых было даже в хорошо вакуумированном сосуде предостаточно. Эти атомарные соединения могли обладать и парамагнетизмом, а не присущим серебру диамагнетизмом.
Платина – парамагнетик и атомарное серебро могло образовывать некие амальгамные соединения с разогретой до 2200 градусов платиной.

Это, разумеется, лишь предположения, призванные объяснить эффект раздвоение осаждённых на пластине полосок.

Источник: proza.ru

9.2. Опыты Штерна и Герлаха. Спин электрона и спиновое квантовое число

В 1922 г. в опытах Штерна 1 и Герлаха 2 по измерению магнитных моментов атомов водорода было установлено, что при прохождении пучка атомов сквозь неоднородное магнитное поле этот пучок расщепляется на два пучка. На рис. 9.2,а показана схема установки и на рис. 9.2,б наблюдаемое расщепление пучка атомов серебра в неоднородном магнитном поле на 2 пучка.

Рис. 9.2

По классической теории на атом в неоднородном магнитном поле действует сила, для которой

где mz – проекция магнитного момента атома на направление магнитного поля (ось «ОZ»), что привело бы лишь к уширению пучка.

Из рассмотренного нами решения уравнения Шредингера для атома водорода следует, что невозбужденные атомы находятся в s-состоянии, в котором момент импульса электрона равен нулю. Магнитный момент атома, связанный с орбитальным движением электрона, пропорционален механическому моменту, поэтому он также равен нулю, и магнитное поле не должно оказывать влияния на движение атомов водорода в основном состоянии, т.е. расщепления быть не должно.

Однако опыты Штерна и Герлаха экспериментально доказали, что проекции магнитных моментов атомов на направление поля квантуются, т.е. принимают дискретные значения. Для объяснения этого явления в 1925 г. Уленбек 1 и Гаудсмит 2 предположили, что электрон обладает собственным механическим моментом импульса – спином.

Как было доказано позже, спин – квантовая величина, не связанная с движением электрона в пространстве. Спин – это внутреннее неотъемлемое свойство электрона, подобное заряду и массе, для которого нет классического аналога.

Наличие спина электрона было экспериментально подтверждено и целым рядом других опытов.

Таким образом, так как у электрона есть спин то с ним оказывается связанным некоторый собственный магнитный моментpms. В соответствии с выводами квантовой механики спин квантуется по закону

Вектор может принимать 2s + 1 ориентаций. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2s + 1 = 2, поэтому

Проекция спина на направление магнитного поля также является квантованной величиной и определяется выражением:

где ms – магнитное спиновое квантовое число, принимающее только два значения:

Таким образом, для полного описания состояния электрона в атоме необходимы 4 квантовых числа: главное n, орбитальное l, магнитное ml и магнитное спиновое ms.

9.3. Принцип Паули и заполнение электронных оболочек атомов. Спектры атомов

В сложных атомах присутствует группа электронов, т.е. группа тождественных частиц. По квантовой механике тождественные частицы неразличимы, так как определяется лишь их вероятность || 2 .

Принцип неразличимости тождественных частиц, вытекающий из квантовой механики, записывается следующим образом:

Возможны два случая:

1) Ψ(x1, x2) = +Ψ(x2, x1) – симметричная волновая функция для частиц, которые называются бозонами (описываются статистикой Бозе 1 Эйнштейна). К ним относятся частицы с целым спином s= 0, 1, 2 и т.д.: π, hν, …;

2) Ψ(x1, x2) =  Ψ(x2, x1) – антисимметричная волновая функция для частиц, которые называются фермионами (описывают-

ся статистикой Ферми 2 Дирака 3 ). К ним относятся частицы с полуцелым спином s= 1/2, 3/2 и т.д.: e, p, n… .

Для фермионов в квантовой механике Паули 4 был установлен (в 1925 г.) общий принцип: в системе одинаковых фермионов любые два из них не могут одновременно находиться в одном и том же состоянии. (Следует отметить, что по квантовой механике число бозонов не лимитируется.)

Как было показано выше, в атоме присутствуют электроны, а их состояния различаются по четырем квантовым числам: n, l, ml, ms. Принцип Паули в простейшей форме для электронов в атоме может быть сформулирован таким образом: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел n, l, ml и ms, т.е.

Z (n, l, ml, ms) = 0 или 1,

где Z(n, l, ml, ms) – число электронов, находящихся в квантовом состоянии, описываемом набором четырех квантовых чисел n, l, ml и ms.

Так как данному n соответствует n 2 различных состояний, отличающихся значениями l и ml, а квантовое число msможет принимать лишь два значения, то максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом n, равно 2n 2 , так как

.

В соответствии с этим выражением, т.е. с принципом Паули, происходит заполнение электронных оболочек в атомах и строится вся периодическая система элементов Д.И. Менделеева 1 . При этом учитывается и принцип минимума энергии электрона в энергетических состояниях (особенно начиная с элементов K, Ca,…).

В зависимости от строения электронных оболочек атомы и, следовательно, молекулы обладают различными оптическими спектрами, которые свидетельствуют о строении атомов и молекул, а также имеют широкое практическое применение.

Источник: studfile.net

Компьютерное моделирование опыта Штерна-Герлаха, изучение поведения атомов в неоднородном магнитном поле, измерение магнитного момента атомов

Цель работы: компьютерное моделирование опыта Штерна –
Герлаха, изучение поведения атомов в неоднородном магнитном поле, измерение магнитного момента атомов.

8.1. Пространственное квантование

В теоретическом введении к главе 3 приведены сведения о механическом и магнитном моментах атомов (этот материал следует предварительно изучить). Полные моменты электронной оболочки атома обусловлены частично орбитальным движением электронов, частично – их спинами. Как модули, так и проекции момента импульса и магнитного момента квантуются, причем единицей квантования момента импульса служит постоянная Планка ħ, а магнитного момента – магнетон Бора μB:

, ;

,

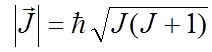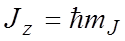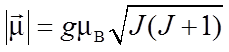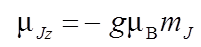
где J – квантовое число полного момента, а g – множитель Ланде. Число J принимает одно из значений

,

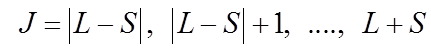
где S– спиновое квантовое число, а L– орбитальное квантовое число всей электронной оболочки. В свою очередь, магнитное квантовое число mJ может принимать одно из значений

.

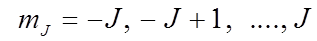
Очевидно, общее количество этих значений, а следовательно и проекций вектора момента с определенным Jравно 2 J+ 1. Множитель Ланде g зависит от орбитального и спинового вкладов в полный момент и определяется по формуле (36) введения:

.

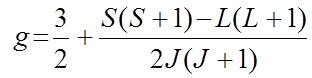
Квантование проекций означает, что если атом находится в магнитном поле, то угол θ между вектором момента импульса и направлением вектора магнитной индукции B может принимать лишь одно из 2 J+ 1 значений. Согласно (8.1) и (8.3) разрешены только те углы θJz, для которых проекция момента импульса кратна постоянной Планка, а косинус определяется соотношением:

.

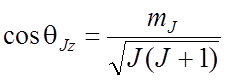
Никакие иные ориентации магнитного и механического моментов в пространстве не реализуются. Этот эффект принято называть пространственным квантованием. Разумеется, речь идет не о квантовании самого пространства, а лишь о пространственных аспектах поведения моментов микрочастиц. При этом, с наглядной точки зрения, момент атома, подобно гироскопу, совершает прецессию с частотой

.

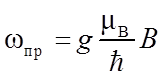
В ходе такой прецессии векторы механического и магнитного моментов описывают коническую поверхность с углом θJz между ее образующей и осью, которая совпадает с направлением вектора магнитной индукции.

8.2. Как обнаружить пространственное квантование?

Силовое воздействие внешнего магнитного поля на атом, обладающий магнитным дипольным моментом, подобно его действию на миниатюрную магнитную стрелку. Если поле однородно, то на магнитный диполь будет действовать только момент силы, стремящийся развернуть его вдоль направления вектора магнитной индукции.

Однако в неоднородном магнитном поле появится еще и сила, величина которой зависит от угла между диполем и градиентом магнитной индукции. Под действием этой силы при прохождении через неоднородное магнитное поле пучок таких атомов будет отклоняться.

Если на ориентацию атомных магнитных моментов не наложено никаких ограничений, как это было бы согласно классическим представлениям, то величины отклонений отдельных атомов будут непрерывным образом распределены в некотором интервале, и пучок окажется размытым. Наоборот, если «атомные магнитики» могут ориентироваться только под определенными углами к направлению магнитного поля, как это предсказывает квантовая теория, то будет возможно только некоторое ограниченное число отклонений, и пучок расщепится на несколько компонент. Именно это и имел в виду Отто Штерн в опубликованной в 1921 году статье: «Выяснить, какая теоретическая концепция – квантовая или классическая – является правильной, можно с помощью эксперимента, в принципе совсем простого. Требуется только исследовать отклонение, испытываемое пучком атомов в достаточно неоднородном магнитном поле».

8.3. Опыт Штерна – Герлаха

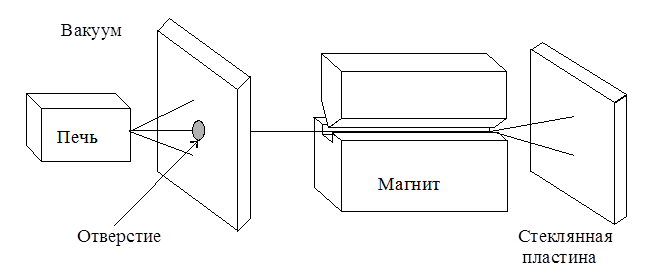
Вскоре Отто Штерн и его сотрудник Вальтер Герлах выполнили запланированный эксперимент. Схема опыта Штерна – Герлаха показана на рис. 8.1. Опыт проводился в вакууме, чтобы пучок атомов не разрушался из-за рассеяния на молекулах газа.

Путем испарения в миниатюрной печке создавался поток атомов серебра, который затем коллимировался двумя диафрагмами, проходил между полюсами магнита специальной конфигурации, формировавшими неоднородное магнитное поле, и попадал на стеклянную пластинку, образуя на ней осадок. Один из полюсных наконечников магнита имел вид призмы с острым ребром (лезвиеобразный), а вдоль другого была выточена канавка.

Нетрудно получить соотношения для количественной оценки величины отклонения атомов. В неоднородном магнитном поле на атомы действует сила

.

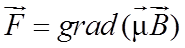
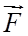
Поскольку и вектор магнитной индукции и его градиент направлены перпендикулярно к направлению движения атомов, сила , создающая их поперечное отклонение, будет иметь лишь компоненту Fz , равную

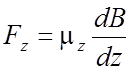
Под действием этой силы атом массы M, движущийся параллельно лезвиеобразному полюсу, приобретет ускорение вдоль оси z, равное Fz / M, и за время прохождения области поля t1 он отклонится от своего начального направления на величину Δz1 = (Fz / M) t1 2 /2. Время t1 равно отношению длины магнитных полюсов a, к скорости v атома: t1 = a/ v. Следовательно, поперечное отклонение атома при вылете из области поля составит:

Похожие материалы

• Магнитный момент атома. Атом в магнитном поле
• Определение дисперсии и разрешающей способности спектрографа
• Определение параметров потенциальной ямы и потенциала ионизации атома ксенона на основе эффекта Рамзауэра

Источник: vunivere.ru