Как самым простым способом не применяя никаких приборов определить больше или меньше 1 г см

§ 5. Точность и погрешность измерений Всякое измерение может быть выполнено с большей или меньшей точностью. В качестве примера рассмотрим измерение длины

Как узнать с помощью опыта не пользуясь весами и мензуркой больше или меньше единицы плотность ученической ручки?

Как узнать с помощью опыта не пользуясь весами и мензуркой больше или меньше единицы плотность ученической ручки.

Если всплывет то плотность меньше плотности воды и наоборот.

Как узнать плотность и объем своего тела зная что мой вес 50?

Как узнать плотность и объем своего тела зная что мой вес 50.

Помогите?

Две одинаковые мензурки с разными жидкостями уравновешенны на рычажных весах.

В первой цензуре вода.

Определите плотность жидкости во второй мензурке.

Никаких компромиссов. От топ переговорщика ФБР | Крис Восс

Как с помощью только одной мензурки определить плотность небольшого куска древесины?

Как с помощью только одной мензурки определить плотность небольшого куска древесины?

Как с помощью только одной мензурки определить плотность небольшого куска древесины?

Как с помощью только одной мензурки определить плотность небольшого куска древесины.

Как с помощью только одной мензурки определить плотность древесины предложенного небольшого тела?

Как с помощью только одной мензурки определить плотность древесины предложенного небольшого тела?

Как, не пользуясь весами, можно показать, что массы двух бильярдных шаров одинаковы?

Как, не пользуясь весами, можно показать, что массы двух бильярдных шаров одинаковы?

Как жто проверить с помощью весов?

Изменится ли вес тела при его погружении в воду?

Изменится ли вес тела при его погружении в воду?

Как с помощью только одной мензурки определить плотность древесины предложенного небольшого тела?

Как узнать экспериментально (не пользуясь весами и мензуркой) больше или меньше плотность воды плотность ученической резинки?

Как узнать экспериментально (не пользуясь весами и мензуркой) больше или меньше плотность воды плотность ученической резинки.

Как найти плотность стеклянной колбочки с помощью мензурки с водой без использования весов?

Как найти плотность стеклянной колбочки с помощью мензурки с водой без использования весов?

Лабораторная по физике.

10 Секретных Точек на Теле, Которые Наделят Тебя Суперсилой

Какие физические величины измеряют с помощью мензурки, линейки, секундомера, спидометра, термометра, весов?

Какие физические величины измеряют с помощью мензурки, линейки, секундомера, спидометра, термометра, весов.

На этой странице сайта размещен вопрос Как узнать с помощью опыта не пользуясь весами и мензуркой больше или меньше единицы плотность ученической ручки? из категории Физика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

На 74 градусов. Наверное так.

Площадь верхнего основания конуса не имеет никакого значения. Со стороны нижнего основания на стол действует сила mg, распределённая по площади Sa Единственно, надо площадь перевести в квадратные метры Sa = 4 см² = 4 / 10000 м² = 0, 0004 м² P = mg /..

Поскольку за ПЕРИОД грузик пройдет расстояние, равное четырем амплитудам: L₀ = 4 * 3 = 12 см или 0, 12 м то число колебаний: n = L / L₀ = 0, 36 / 0, 12 = 3 Ответ: 3 колебания.

Q = λ * m = 4 * 330000 = 1320000Дж или 1320 кДж.

Решение Q = m * λ Отсюда находим массу m = Q / λ = 0, 1 кг 100 грамм свинца.

V = 72 км / ч = 20 м / с; = V² / R = 20² / 500 = 0, 8 м / с²; N = m(g — ) = 500×(10 — 0, 8) = 4600 Н (4500, если брать g за 9. 8 м / с²).

Правильный ответ это б.

0, 3 * m1 = N * 0, 2 0, 1 * N = 0, 3 * M m1 = 2M M = 1, 2 кг.

Потому что перемещение, cкорость, ускорение — величины векторные и работать с векторами труднее чем с проекциями.

Ответ: Объяснение: Дано: S₁ = S / 4V₁ = 72 км / чS₂ = 3·S / 4V₂ = 15 м / с____________Vcp -? Весь путь равен S. Время на первой четверти пути: t₁ = S₁ / V₁ = S / (72·4) = S / 288 чВремя на остальной части пути: t₂ = S₂ / V₂ = 3·S / (15·4) = 3..

И можно ли его разбить, например, обычным молотком? Все очень и очень просто, но давайте начнем по порядку. Алмаз — действительно самый твёрдый минерал на нашей Планете и имеет по шкале твердости Мооса максимальные 10 баллов. А теперь перейдем к самому интересному. Как получить порошок или крошку из алмаза, если это самое твердое на Земле соединение? И как тогда можно разрушить его в домашних условиях? Тут все очень просто. Для начала нужно определить различия между терминами «твердость» и «прочность». Твердость — это способность материала сопротивляться проникновению в него другого материала, а прочность — это его способность не разрушаться под воздействием внешних сил.

Как самым простым способом не применяя никаких приборов определить больше или меньше

Всякое измерение может быть выполнено с большей или меньшей точностью.

В качестве примера рассмотрим измерение длины ручки демонстрационным метром с сантиметровыми делениями (рис. 14).

Вначале определим цену деления линейки. Она будет равна 1 см.

Если верхний конец ручки совместить с нулевым штрихом, то нижний будет находиться между 11 и 12 штрихами, но ближе к 11.

Какое же из этих двух значений следует принять за длину ручки? Очевидно, то, которое ближе к истинному значению, т. е. 11 см.

Считая, что длина ручки 11 см, мы допустили неточность, так как ручка чуть длиннее 11 см.

В физике допускаемую при измерении неточность называют погрешностью измерений.

Погрешность измерения не может быть больше цены деления шкалы измерительного прибора.

В нашем случае погрешность измерения ручки не превышает 1 см. Если такая точность измерений нас не удовлетворяет, то можно произвести измерения с большей точностью. Но тогда придётся взять масштабную линейку с миллиметровыми делениями, т. е. с ценой деления 1 мм.

В этом случае длина ручки окажется равной 11,2 см.

Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.

Чем меньше цена деления, тем больше точность измерения.

Точность измерения зависит также от правильного применения измерительного прибора, расположения глаза при отсчёте по прибору.

Вследствие несовершенства измерительных приборов и наших органов чувств при любом измерении получаются лишь приближённые значения, несколько большие или меньшие истинного значения измеряемой величины.

Во время выполнения лабораторных работ или просто измерений следует считать, что погрешность измерений равна половине цены деления шкалы измерительного прибора.

Измерим длину карандаша. Нулевую отметку линейки совместим с одним концом карандаша, а другой её конец окажется вблизи 14 см. Цена деления линейки 1 мм, тогда погрешность измерения будет равна 0,5 мм или 0,05 см.

Следовательно, длину карандаша можно записать в виде

где I — длина карандаша.

Истинное значение длины карандаша находится в интервале от 13,95 см до 14,05 см.

При записи величин, с учётом погрешности, следует пользоваться формулой

где А — измеряемая величина, а — результат измерений, Δа — погрешность измерений (Δ — греч. буква «дельта»).

Вопросы

1. Как понимать выражение «измерить длину с точностью до 1 мм»?
2. Можно ли линейкой, имеющей сантиметровые деления, измерить длину с точностью до 1 мм?
3. Какова связь точности измерений с ценой деления шкалы прибора?
4. Какой формулой необходимо пользоваться при записи физических величин с учётом погрешности?

Задание

1. Измерьте линейкой с миллиметровыми делениями длину и ширину вашего учебника. Запишите результаты с учётом погрешности измерения.

2. Пользуясь рисунком 11, б, определите погрешность измерения термометра.

3. Измерьте линейкой с миллиметровыми делениями длину и высоту картины Л. да Винчи (рис. 15). Запишите результаты измерений с учётом погрешности. Используя Интернет, найдите название картины, её истинный размер и определите масштаб, в котором картина представлена в учебнике.

Сравнение дробей, как правильно

О чем эта статья:

Сравнение дробей с одинаковыми знаменателями

Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.

Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:

Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.

А теперь на примерах.

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.

Давайте разберем наглядный пример сравнения дробей:

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.

Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.

Сравнение дробей с одинаковыми числителями

Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.

Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.

А теперь наши любимые примеры. Погнали!

Пример 1. Сравните дроби:

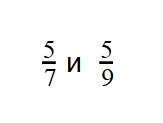
• У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
  9 > 7
  7 10
• Значит дробь с меньшим знаменателем — больше:

Пример 3. Сравните дроби:

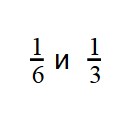
У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
6 > 3
3

Сравнение дробей с разными числителями и разными знаменателями

Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.

Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.

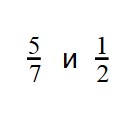
Давайте потренируемся в сравнении дробей.

Пример 1. Сравните дроби:

При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.

Пример 2: Сравните дроби:

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.

• 12 — 7 = 6
  12 — уменьшаемое
  7 — вычитаемое
  5 — разность

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.

Пример 1. Найдите разность:

Вычитаемая дробь меньше уменьшаемой

Пример 2.Найдите разность:

Если знаменатели одинаковые — больше та дробь, числитель которой больше.

Примеры для самопроверки

Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.

Пример 1. Сравните дроби:

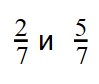
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что

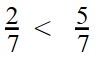
Пример 2. Сравните дроби:

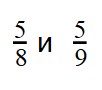
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что

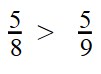
Пример 3. Сравните дроби:

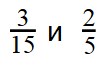
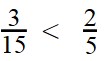
Ответ:.

Но алмаз молотком это варваство. А вот ювелиры разбивают крупные алмазы при поможи кувалдочки. молоток лёгкий и простого зубила. Знаменитый алмаз КуллинанИли Куллиан не помню уже точно разбили на 150 кусков. Три тысячи каратов вроде. Самый большой алмаз в мире был. Так этот ювелир амстердамский полгода изучал его в микроскоп изучая и выявляя микротрещины и линии по которым он должен разбиться. Он нанёс тушью линии и зажав его в приспособлении наставил зубило и ударил. Раздался сильный звон металла и ювелир потерял сознание.