Иногда в тестах ЕГЭ встречаются задачи, в которых при расчете массы конечного раствора необходимо учитывать выпавшее в осадок вещество.
Задача 3.2.
К 1170 г 0,5%-ного раствора хлорида натрия прилили 1275 г 0,2%-ного раствора нитрата серебра. Какова массовая доля нитрата натрия в полученном растворе.
Дано:
масса раствора хлорида натрия: mр_ра(NаС1) = 1170 г;
массовая доля NаС1 в исходном р-ре: (NаС1)в исх р-ре = 0,5% ;
масса раствора нитрата серебра: mр-ра(АgNО3) = 1275 г;
массовая доля АgNО3 в исходном р-ре: (АgNО3)в исх.р-ре= 0,2% ;
Найти: массовую долю NaNО3 в конечном растворе: (NaNО3)в кон..р-ре = ?
Решение 1 :
При смешивании двух исходных растворов, растворенные вещества вступают между собой в реакцию обмена с образованием осадка:
Для наглядности все условие задачи удобно отобразить в виде рисунка:
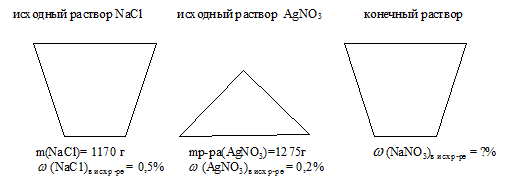
В условии указана информация, позволяющая определить количество вещества каждого из исходных участников реакции. Следовательно, сначала необходимо определить, какое вещество дано в недостатке, и далее по нему вести расчет. Кроме того, при определении массы конечного раствора следует учесть, что АgС1 выводиться из состава раствора в виде осадка.
ДРТ 2021 В14 Химия. Смесь. Система уравнений.
Алгоритм решения данной задачи можно отразить следующей схемой:
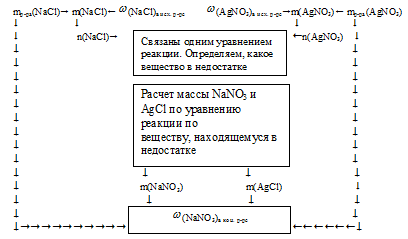
1. Находим массу и количество вещества аNaС1 в первом исходном растворе:
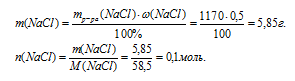
2. Находим массу и количество вещества AgNO3 во втором исходном растворе:
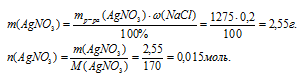
3. Находим, какое вещество дано в недостатке.
Выберем за основу хлорид натрия и определим по уравнению реакции количество АgNО3, которое необходимо для расходования 0,1 моль NаС1.
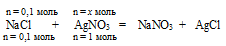
Составляем пропорцию:
на 0,1 моль NаС1 должно расходоваться х моль АgNО3 (по условию)
на 1 моль МаС1 полностью расходуется 1 моль
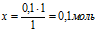
АgNО3 (по уравнению)АgNО3 необходимо для полного расходования всего NаС1.
| n(АgNОз) необходимо | n(АgNОз) дано по условию |
| 0,1 моль > 0,015 моль | |
Нитрат серебра находится в недостатке и расходуется весь в процессе реакции. Поэтому дальнейшие расчеты по уравнению реакции будем проводить по количеству АgNО3.
Нитрат серебра AgNO3 из ювелирного лома.
4. По уравнению реакции, используя полученные значения количества вещества АgNО3, находим массу NaNО3 и АgС1:

5. Находим массовую долю NaNО3 в конечном растворе:
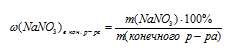
Масса раствора будет складываться из суммы масс исходных двух растворов, из которой вычтена масса осадка АgСl:
mкон. р-ра = mисх. р-ра(NaCl) + mисх. р-ра(AgNO3) – m(AgCl) =
= 1170 + 1275 – 2,15 = 2442,85 г.
Подставляем все данные в соотношение для массовой доли NaNО3:
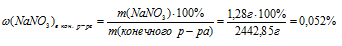
Ответ: (NaNO3)в кон. р-ре = 0,052%.
- Вы здесь:
- Главная

- Задачи

- ЕГЭ-химия

- Вычисление массовой доли нитрата натрия | Химия ЕГЭ-тестовые задачи
Источник: buzani.ru
Массовая доля серебра в нитрате серебра AgNO3 1) 0.64 2) 0.2 3) 0.28 4) 0.57
Получи верный ответ на вопрос «Массовая доля серебра в нитрате серебра AgNO3 1) 0.64 2) 0.2 3) 0.28 4) 0.57 . » по предмету Физика, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!
Новые вопросы по физике
Какую работу надо совершить, чтобы поднять тело массой 10 кг на высоту 2 метра, используя при этом подвижной блок? а) 100 Дж б) 200 Дж в) 10 Дж г) 20 Дж
Чтобы столбик ртути в медицинском термометре опустился, термометр «встряхивают»-двигают вниз, а затем резко останавливают. Какова причина опускания столбика ртути?
По двум парал-ым железнодорожным путям навстречу друг другу равномерно движутся два поезда: грузовой — длиной 630 м — со скоростью 48 км/ч и пассажирский длиной 120 м — со скоростью 102 км/ч.
Брусок массой 900 г соскальзывает с доски, наклоненной к горизонту под углом 30 градусов с ускорением 1,3 м/с2. Каков вес бруска? Как он направлен? Примите ℊ=9,8 м/с.
Частота свободных электромагнитных колебаний в колебательном контуре 20 МГц. Определите частоту колебаний в контуре, если конденсатор емкостью 1 мкФ заменить конденсатором, емкость которого 4 мкФ.
Источник: 4i5.ru
4.3.1. Расчеты с использованием понятия «массовая доля вещества в растворе».

Раствором называют гомогенную смесь двух или более компонентов.
Вещества, смешением которых получен раствор, называют его компонентами.
Среди компонентов раствора различают растворенное вещество, которое может быть не одно, и растворитель. Например, в случае раствора сахара в воде сахар является растворенным веществом, а вода является растворителем.
Иногда понятие растворитель может быть применимо в равной степени к любому из компонентов. Например, это касается тех растворов, которые получены смешением двух или более жидкостей, идеально растворимых друг в друге. Так, в частности, в растворе, состоящем из спирта и воды, растворителем может быть назван как спирт, так и вода. Однако чаще всего в отношении водосодержащих растворов традиционно растворителем принято называть воду, а растворенным веществом — второй компонент.
В качестве количественной характеристики состава раствора чаще всего используют такое понятие, как массовая доля вещества в растворе. Массовой долей вещества называют отношение массы этого вещества к массе раствора, в котором оно содержится:
где ω(в-ва) – массовая доля вещества, содержащегося в растворе (г), m(в-ва) – масса вещества, содержащегося в растворе (г), m(р-ра) – масса раствора (г).
Из формулы (1) следует, что массовая доля может принимать значения от 0 до 1, то есть составляет доли единицы. В связи с этим массовую долю можно также выражать в процентах (%), причем именно в таком формате она фигурирует практически во всех задачах. Массовая доля, выраженная в процентах, рассчитывается по формуле, схожей с формулой (1) с той лишь разницей, что отношение массы растворенного вещества к массе всего раствора умножают на 100%:
Для раствора, состоящего только из двух компонентов, могут быть соответственно рассчитаны массовые доли растворенного вещества ω(р.в.) и массовая доля растворителя ω(растворителя).
Массовую долю растворенного вещества называют также концентрацией раствора.
Для двухкомпонентного раствора его масса складывается из масс растворенного вещества и растворителя:
Также в случае двухкомпонентного раствора сумма массовых долей растворенного вещества и растворителя всегда составляет 100%:
Очевидно, что, помимо записанных выше формул, следует знать и все те формулы, которые напрямую из них математически выводятся. Например:
Также необходимо помнить формулу, связывающую массу, объем и плотность вещества:
а также обязательно нужно знать, что плотность воды равна 1 г/мл. По этой причине объем воды в миллилитрах численно равен массе воды в граммах. Например, 10 мл воды имеют массу 10 г, 200 мл — 200 г и т.д.
Для того чтобы успешно решать задачи, помимо знания указанных выше формул, крайне важно довести до автоматизма навыки их применения. Достичь этого можно только прорешиванием большого количества разнообразных задач. Задачи из реальных экзаменов ЕГЭ на тему «Расчеты с использованием понятия «массовая доля вещества в растворе»» можно порешать здесь.
Примеры задач на растворы
Пример 1
Рассчитайте массовую долю нитрата калия в растворе, полученном смешением 5 г соли и 20 г воды.
Решение:
Растворенным веществом в нашем случае является нитрат калия, а растворителем — вода. Поэтому формулы (2) и (3) могут быть записаны соответственно как:
Из условия m(KNO3) = 5 г, а m(Н2O) = 20 г, следовательно:
Пример 2
Какую массу воды необходимо добавить к 20 г глюкозы для получения 10%-ного раствора глюкозы.
Решение:
Из условий задачи следует, что растворенным веществом является глюкоза, а растворителем — вода. Тогда формула (4) может быть записана в нашем случае так:
Из условия мы знаем массовую долю (концентрацию) глюкозы и саму массу глюкозы. Обозначив массу воды как x г, мы можем записать на основе формулы выше следующее равносильное ей уравнение:
Решая это уравнение находим x:
т.е. m(H2O) = x г = 180 г
Пример 3
150 г 15%-ного раствора хлорида натрия смешали со 100 г 20%-ного раствора этой же соли. Какова массовая доля соли в полученном растворе? Ответ укажите с точностью до целых.
Решение:
Для решения задач на приготовление растворов удобно использовать следующую таблицу:
1-й раствор
2-й раствор
3-й раствор
mр.в.
mр-ра
ωр.в.
где mр.в., mр-ра и ωр.в. — значения массы растворенного вещества, массы раствора и массовой доли растворенного вещества соответственно, индивидуальные для каждого из растворов.
Из условия мы знаем, что:
Вставим все эти значения в таблицу, получим:
1-й раствор
2-й раствор
3-й раствор
mр.в.
mр-ра
ωр.в.
Нам следует вспомнить следующие формулы, необходимые для расчетов:
Начинаем заполнять таблицу.
Если в строчке или столбце отсутствует только одно значение, то его можно посчитать. Исключение — строчка с ωр.в., зная значения в двух ее ячейках, значение в третьей рассчитать нельзя.
В первом столбце отсутствует значение только в одной ячейке. Значит мы можем рассчитать его:
Аналогично у нас известны значения в двух ячейках второго столбца, значит:
Внесем рассчитанные значения в таблицу:
1-й раствор
2-й раствор
3-й раствор
mр.в.
mр-ра
ωр.в.
Теперь у нас стали известны два значения в первой строке и два значения во второй строке. Значит мы можем рассчитать недостающие значения (m(3)р.в. и m(3)р-ра):
Внесем рассчитанные значения в таблицу, получим:
1-й раствор
2-й раствор
3-й раствор
mр.в.
mр-ра
ωр.в.
Вот теперь мы вплотную подобрались к расчету искомой величины ω(3)р.в.. В столбце, где она расположена, известно содержимое двух других ячеек, значит мы можем ее рассчитать:
Пример 4
К 200 г 15%-ного раствора хлорида натрия добавили 50 мл воды. Какова массовая доля соли в полученном растворе. Ответ укажите с точностью до сотых _______%
Решение:
Прежде всего следует обратить внимание на то, что вместо массы добавленной воды, нам дан ее объем. Рассчитаем ее массу, зная, что плотность воды равна 1 г/мл:
Если рассматривать воду как 0%-ный раствор хлорида натрия, содержащий соответственно 0 г хлорида натрия, задачу можно решить с помощью такой же таблицы, как в примере выше. Начертим такую таблицу и вставим известные нам значения в нее:
1-й раствор
2-й раствор
3-й раствор
mр.в.
mр-ра
ωр.в.
В первом столбце известны два значения, значит можем посчитать третье:
Во второй строчке тоже известны два значения, значит можем рассчитать третье:
Внесем рассчитанные значения в соответствующие ячейки:
1-й раствор
2-й раствор
3-й раствор
mр.в.
mр-ра
ωр.в.
Теперь стали известны два значения в первой строке, значит можем посчитать значение m(3)р.в. в третьей ячейке:
Источник: scienceforyou.ru