Ханойская башня на пальцах
Пообщавшись с некоторыми знакомыми программистами, внезапно обнаружил, что не все знают про Ханойскую башню, а среди тех кто знает — мало кто понимает как решается эта задача.
Википедия по этому поводу пишет очень строго, по делу, и ничего не объясняет. Мол принимайте как прописную истину. Поэтому понять как она решается — сходу трудновато. А ведь задача очень простая, и между тем интересная в программировании и математически.
В статье будет много картинок. Объяснение как решать задачу рекурсивно и как она решается бинарным поиском.
В общем статья посвящается тем смелым, кто пока еще боится Ханойской башни, но хочет перестать её бояться.
Правила игры
Они очень просты. Есть 1 пирамидка с дисками разного размера, и еще 2 пустые пирамидки. Надо переместить диски с одной пирамидки на другую. Перекладывать можно только по одному диску за ход. Складывать диски можно только меньший на больший.
Итак у нас есть вот такая пирамидка:
Как собрать кольцо-головоломку: четырёхчастный и семичастный варианты
И нам надо переложить её скажем на среднюю ось.
Если начать решать задачу не с начала, а с конца — она оказывается очень простой. Давайте подумаем. Чтобы переложить пирамидку на вторую ось — нам надо переложить самый нижний диск, а сделать это можно только когда 4 верхних диска будут на третьей оси:
Для того, чтобы переложить 4 диска на третью ось нужно по сути решить ту же задачу, но для 4-х дисков. То есть на третью ось мы можем переложить 4-ый диск только тогда, когда у нас 3 диска на второй оси:
Чувствуете рекурсию?
Перекладывание стека из 5 дисков — это:
1. Перекладывание стека из 4х дисков на независимую ось
2. Перекладывание 5-го диска на нужную нам ось
3. Перекладывание стека из 4х дисков на нужную нам ось
В свою очередь перекладывание стека из 4 дисков — это:
1. Перекладывание стека из 3х дисков на независимую ось
2. Перекладывание 4-го диска на нужную нам ось
3. Перекладывание стека из 3х дисков на нужную нам ось
Рекурсивная реализация
Итак я описал модуль с типами башенок:
TTower — структура описывающая башню. В ней в RingCount хранится количество фактически одетых колец на башне. Размер колец хранится в массиве Rings от 1 и до MaxRingCount. Поскольку у нас 3 башни — то был объявлен тип TTowers = array [0..2] of TTower;
Так же с башни можно переложить верхее кольцо на другую с помощью функции MoveRing. Функция проверяет корректность операции через Assert-ы.
Само же решение башни находится в файле проекта:
Алгоритмическая сложность
Мы легко можем подсчитать, сколько действий нам понадобится, чтобы переместить пирамидку.
Если мы перемещаем стек из одного диска — то нам нужно 1 действие.
Если стек из двух — то 1 * 2 (переместить дважды стек из одного диска ) + 1 (перемещаем последний диск)
Если из трех ((1 * 2) + 1) * 2 + 1
Из пяти: (((((1 * 2) + 1) * 2 + 1) * 2 + 1) * 2 + 1)
Решение головоломки Кольцо Leonardo Hanayama
Итак каждая операция увеличивает в 2 раза + 1 кол-во перемещений. Раскрыв скобки для n операций — получаем:
От суммы можно избавиться, ибо она равна:
p.s. я избавился от суммы в голове, вспомнив сумму членов бесконечно убывающей геометрической прогрессии, но я надеюсь математики покажут как правильно записать эти преобразования
Итого у нас после всех преобразований вышло:
То есть если нам захочется странного, например записать решение ханойской башни для 64 дисков, то никаких современных носителей информации нам не хватит. В действительности — нам вообще не надо ничего никуда записывать. Это все равно, что записывать все числа от 0 до +бесконечности, чтобы потом их использовать, потому что решение ханойской башни — это фрактал.
Фрактальная природа
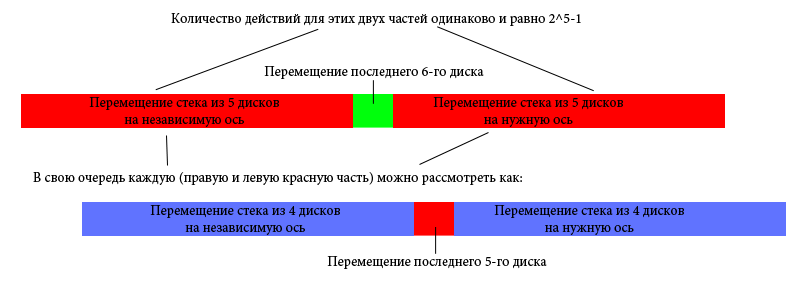
Да да. Решение ханойской башни имеет фрактальную природу. Давайте посмотрим. Допустим у нас каждое действие записывается в строку. Тогда для башни из 6 дисков можно записать это как-то так:
Ну а поскольку это фрактал — то мы можем легко назвать любую операцию зная лишь её порядковый номер. И даже более, мы можем в точности восстановить положение всех дисков на момент любой операции.
Бинарный алгоритм
Итак, мы знаем точное количество операций, а так же знаем индекс операции, для которой мы хотим восстановить состояние.
Допустим у нас башня из 6 дисков (перемещаем как обычно, с 1-ой на среднюю ось), а значит операций у нас 2^6-1 = 63. Допустим нам требуется восстановить состояние для 49-ой операции.
Делим целочисленно 63 на 2. Получается 31. Это индекс операции, на которой будет перемещен 6-ой диск:
У нас 49-ый индекс операции. Это значит что 6-ой диск уже лежит на средней оси. Кроме того, поскольку мы находимся в правой части, то пятый диск у нас лежит либо на 3-ей оси, либо на 2-ой. Для того чтобы мы могли работать с башней по тому же алгоритму — отнимаем от 49-ой операции 32, находим индекс подоперации. Это 17.
Для перемещения стека из 5 дисков нужна 31 операция, при этом 5-ый диск перемещается на 16-ю операцию и с 3-ей оси на 2-ую.
Итак число 17 лежит правее:
А это значит что диск 5 уже перемещен на вторую ось.
По аналогии восстанавливаем положение остальных дисков.
Реализация (бинарный способ)
Я добавил красивую отрисовку башенок. Согласитесь, скучно смотреть в консольный лог. Поэтому реализация разрослась, и я прикреплю полный проект (исходник + бинарник) в конце статьи. Здесь же приведу
Треугольник Серпинского

Я хотел бы еще вскользь упомянуть интересную особенность. Если все возможные перемещения колец собрать в граф, то для каждого узла будет чаще всего по 3 связи. Все узлы и связи можно красиво расположить в форме треугольника. Треугольника Серпинского:
Подробнее об этом сказано на википедии вот тут. Что в общем не удивительно, потому что мы уже знаем фрактальную природу решения 😉
Итого
Я постарался показать, насколько иногда просто может решаться казалось бы не совсем очевидная задача. Более того, при внимательном изучении можно внезапно обнаружить совершенно другие интересные алгоритмы решения задачи, открывающие новые возможности. Ищите разные подходы, экспериментируйте, анализируйте. Ведь мы на то и программисты.
Спасибо тем кто дочитал, и кому статья понравилась. Прикрепляю демо пример, в котором можно поелозить трекбаром, и посмотреть на то как перекладываются башенки.
Как собрать головоломку кольцо
Карманные головоломки придумали несколько сотен лет назад. В наше время они не теряют своей актуальности. Современный рынок предлагает большое многообразие головоломок из различных материалов. Одной из таковых является небезызвестное «кольцо», сущность которой заключается в сборке трех (или более) колец воедино и в их последующем разъединении.

- Как собрать головоломку кольцо
- Как собрать головоломку «Звезда»
- Как решить металлические головоломки
Стандартная головоломка «кольцо» состоит из 4 частей. При работе с ней вам потребуется ровная поверхность, на которой вы смогли бы ее разложить, и яркое освещение: все детали головоломки должны быть хорошо видны.
Разобрать уже собранную конструкцию из четырех колец можно без особого труда: например, швырнув с небольшой силой о поверхность стола. Сразу после этого вы со всей ясностью увидите перед собой четыре кольца, сплетенных в один «узел». Обычно в таких головоломках есть два типа колец: кольца с «галочками» и кольца с небольшим изгибом (кольца-«синусоиды»).
Возьмите в руки два кольца с «галочками» наложите их друг на друга так, чтобы изделие с большей шириной «галочки» оказалась под кольцом с меньшим размером «галочки». Если вы все сделали правильно, то ощутите, что все части головоломки встали на свое место. При этом так называемая задняя часть колец (та, что располагается обычно с внутренней стороны ладони), будет представлять собой две тонкие параллельные друг другу линии. Зафиксируйте это положение.
Внимательно рассмотрите два кольца с небольшими изгибами. На поверхности одного из них вы увидите небольшой проем (впадинку), который будет необходим для совмещения этого типа частей головоломки. Кольцо с небольшим изгибом и «впадинкой» наложите рисунком вверх поверх двух колец с «галочками» так, чтобы все три детали расположились ровно. (О том, что вы на правильном пути, будут свидетельствовать три параллельные линии, расположенные на противоположной от рисунка колец стороне).
Рассмотрите рисунок, полученный от совмещения трех колец, повнимательнее и увидите одну линию – «впадинку» для четвертого элемента головоломки. Наложите четвертое кольцо также – рисунком поверх предыдущих трех. Вставьте его заднюю часть внутрь так, чтобы эта линия плотно заполнила недостающее пространство среди трех предыдущих колец. Головоломка собрана!
Источник