
А если немного отойти от правил? Например построить кольцо Мёбиуса, поверхность которого не будет пересекать образующую ось тора?
Для этого нужно взять за основу ленту (поверхность) волнообразного профиля в сечении, как показано на Рис.1 и Рис.2 (внизу под спойлерами показаны их изображения). Затем, уже традиционно, берём такой профиль и ведём его по кругу поворачивая один из краёв на угол, необходимый для построения односторонних колец — 180 град, 540 град, 900 град и т.д. Как показано на Рис.3. В данном конкретном случае, для наглядности, берём угол поворота профиля равный 180 градусам.
В результате получаем кольцо, которое изображено на Рис.4. Такой — волнообразный профиль кольца естественно не сомкнётся по всей своей боковой поверхности. Волновые, изогнутые части профиля не сомкнутся. Но если проследить внимательно полученное кольцо, то мы обнаружим, что данная модель кольца всё равно является односторонней. Если провести образующую ось тора Рис.5 (выделена синим цветом), то наглядно видно, что кольцо с таким профилем не будет его пересекать.
Лента МЕБИУСА — простейшая топологическая односторонняя поверхность.
Далее построим тор (выделен прозрачной текстурой бледно-бирюзового цвета), диаметр образующей окружности которого будет равен ширине профиля кольца. Таким образом мы впишем наше одностороннее кольцо в тор Рис.6 и увидим, что своим краем наше кольцо Мёбиуса описывает тор полностью. В сечении на Рис.7 мы видим, что край нашего кольца Мёбиуса плотно прилегает к поверхности тора.
Вывод — мы построили, хотя и не обычное, но всё же одностороннее кольцо Мёбиуса торового типа без пересечения образующей оси тора.
Источник: moebius.ucoz.com
Лента Мебиуса — удивительное открытие
Практически все знают, как выглядит символ бесконечности, напоминающий перевернутую восьмерку. Этот знак называют еще «лемниската», что с древнегреческого означает лента. Представьте себе, что символ бесконечности очень похож на реально существующую математическую фигуру. Знакомьтесь, Лента Мебиуса!
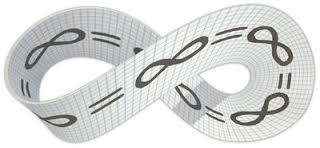
Что такое Лента Мебиуса?
Лента Мебиуса (или ее еще называют петля Мебиуса, лист Мебиуса и даже кольцо Мебиуса) – одна из наиболее известных в математике поверхностей. Петля Мебиуса — это петля с одной поверхностью и одним краем.
Чтобы понять, о чем идет речь, и как такое может быть, возьмите лист бумаги, вырежьте полоску прямоугольной формы и в момент соединения ее концов перекрутите на 180 градусов один из них, после чего соедините. Разобраться в том, как сделать ленту Мебиуса поможет картинка ниже.
Как разрезать бесконечность?! Режем ленту Мёбиуса. Фокус который способен удивить!
Что же такого примечательного в ленте Мебиуса?
Лента Мебиуса – пример неориентируемой односторонней поверхности с одним краем в обычном трёхмерном Евклидовом пространстве. Большинство предметов являются ориентируемыми, имеющими две стороны, например, лист бумаги.
Как тогда лента Мёбиуса может быть неориентируемой, односторонней поверхностью — скажете вы, ведь бумага, из которой она сделана имеет две стороны. А вы попробуйте взять маркер и заполнить цветом одну из сторон ленты, в конечном итоге вы упретесь в начальную позицию, причем вся лента окажется целиком закрашенной, что подтверждает наличие у нее всего одной стороны.
Чтобы поверить в то, что у петли Мебиуса всего один край – проведите пальцем по одному из граней ленты не прерываясь, и Вы точно так же, как и в случае с раскрашиванием, упретесь в точку, с которой начали движение. Удивительно, не правда ли?
Изучением ленты Мёбиуса и множества других интересных объектов занимается – топология, раздел математики, который исследует неизменные свойства объекта при его непрерывной деформации – растяжении, сжатии, изгибе, без нарушения целостности.
Открытие Августа Мебиуса
«Отцом» открывателем этой необычной ленты признан немецкий математик Август Фердинанд Мебиус, ученик Гаусса, написавший не одну работу по геометрии, но прославившийся преимущественно открытием односторонней поверхности в 1858 году.

Удивительным является тот факт, что ленту с одной поверхностью в тот же самый 1858 год открыл другой ученик Гаусса – талантливый математик Иоганн Листинг, придумавший термин «топология» и написавший серию основополагающих трудов по этому разделу математики. Однако свое название необычная лента все же получила по фамилии Мебиуса.

Есть расхожее мнение, что прообразом модели «бесконечной петли» стала неверно сшитая лента служанкой профессора Августа Мебиуса.
На самом деле, лента была открыта давным-давно еще в древнем мире. Одним из подтверждений служит находящаяся во Франции, в музее города Арль древнеримская мозаика с такой же перекрученной лентой. На ней нарисован Орфей, очаровывающий зверей звуками арфы. На фоне неоднократно изображен орнамент с перекрученной лентой.

«Магия» ленты Мебиуса
- Несмотря на кажущееся наличие у листа Мебиуса двух сторон, на самом деле сторона всего одна, и раскрасить в два цвета ленту не получится.
- Если ручкой или карандашом начертить по всей длине петли линию, не отрывая руку от листа, то грифель в конечном итоге остановится в точке, с которой Вы начали чертить линию;
- Примечательные опыты получаются при разрезании ленты, способные удивить, как взрослого, так и ребенка в особенности.
- Для начала склеим ленту Мебиуса, как было рассказано ранее. Затем разрежем ее вдоль по всей длине ровно посередине, как показано ниже:

Вас порядком удивит результат, ведь вопреки ожиданиям в руках останется не два отрезка ленты, и даже не два отдельных круга, но другая, еще более длинная лента. Это уже будет не лента Мебиуса, перекрученная на 180 градусов, а лента с поворотом на 360 градусов.
- Теперь проведем другой эксперимент – сделаем еще одну петлю Мебиуса, после чего отмерим 1/3 ширины ленты и отрежем по этой линии. Результат поразит вас еще больше – в руках останутся две отдельные ленты разных размеров, соединенные вместе, как в цепочке: одна маленькая лента, и более длинная вторая.

У меньшей ленты Мёбиуса будет 1/3 от изначальной ширины ленты, длина L и поворот на 180 градусов. У второй более длинной ленты будет также ширина 1/3 от начальной, но длина 2L, а поворот на 360 градусов.
- Можно и дальше продолжать эксперимент, разрезая получившиеся ленты на еще более узкие, результат увидите сами.
Зачем нужна петля Мебиуса? Применение
Лента Мебиуса – вовсе не абстрактная фигура, нужная лишь для целей математики, она нашла применение и в реальной повседневной жизни. По принципу этой ленты функционирует в аэропорту лента, передвигающая чемоданы из багажного отделения. Такая конструкция позволяет ей служит дольше в связи с равномерным изнашиванием. Открытие Августа Мебиуса повсеместно исполбьзуется в станкостроении. Конструкцию используют для большего времени записи на пленку, а также в принтерах, использующих ленту при распечатке.
Благодаря своей наглядности, петля Мебиуса дает возможность делать современным ученым все новые и новые открытия. С момента обнаружения удивительных свойств петли по всему миру прокатилась волна новых запатентованных изобретений. Например, значительное улучшение свойств магнитных сердечников, изготовленных из ферро-магнитной ленты, намотанных по способу Мебиуса.
Н. Тесла получил патент на многофазную систему переменного тока, использовав намотку катушек генератора по типу петли Мебиуса.
Американский ученый Ричард Дэвис сконструировал нереактивный резистор Мебиуса — способный гасить реактивное (емкостное и индуктивное) сопротивление, не вызывая элекстромагнитных помех.
Лента Мебиуса – широкое поле для Вдохновения
Сложно оценить важность значения открытия петли Мебиуса, которое вдохновило не только большое множество ученых, но и писателей, художников.
Самой известной работой, посвященной ленте Мебиуса считается картина Moebius Strip II, Red Ants или Красные Муравьи голландского художника-графика Маурица Эшера. На картине представлены муравьи, карабкающиеся по петле Мебиуса с обеих сторон, на самом деле сторона всего одна. Муравьи ползут по бесконечной петле друг за другом по одной и той же поверхности.
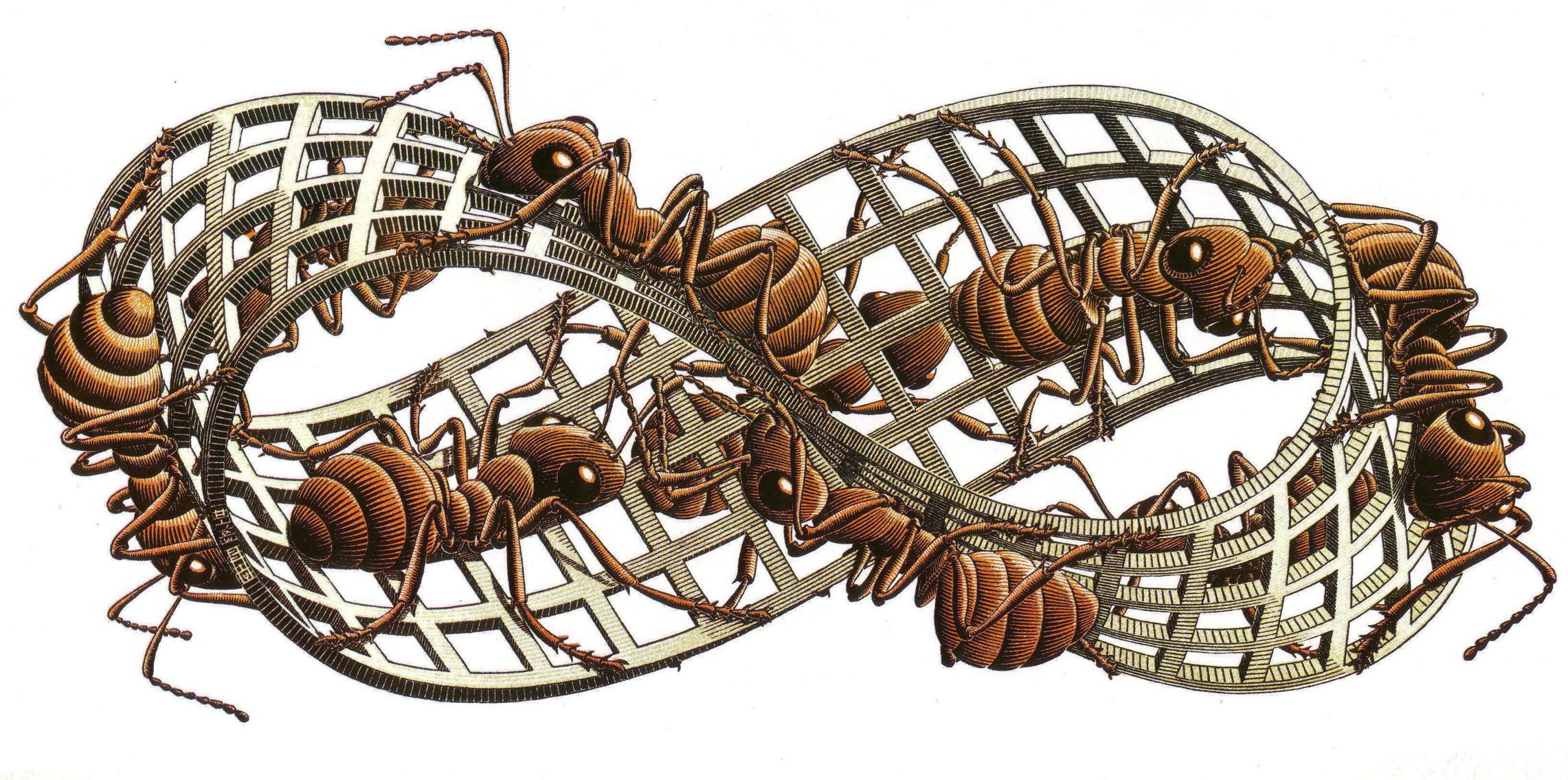
Художник черпал свои идеи из статей и трудов по математике, он был глубоко увлечен геометрией. В связи с чем на его литографиях и гравюрах часто присутствуют различные геометрические формы, фракталы, потрясающие оптические иллюзии.
До сих пор интерес к петле Мебиуса находится на очень высоком уровне, даже спортсмены ввели одноименную фигуру высшего лыжного пилотажа.
По произведению «Лента Мёбиуса» писателя фантаста Армина Дейча снят не один фильм. В форме петли Мебиуса создается огромное множество украшений, обуви, скульптур и многих других предметов и форм.


Лист Мебиуса наложил отпечаток на производство, дизайн, искусство, науку, литературу, архитектуру.

Умы многих людей волновала схожесть формы молекулы ДНК и петли Мебиуса. Существовала гипотеза, которую выдвинул советский цитолог Навашин, что форма кольцевой хромосомы по строению аналогична ленте Мебиуса. На эту мысль ученого натолкнул тот факт, что кольцевая хромосома, размножаясь, превращается в более длинное кольцо, чем в самом начале, или в два небольших кольца, но как в цепи продетых одно в другое, что очень напоминает выше описанные опыты с листом Мебиуса.
В 2015 году группа ученых из Европы и США смогла закрутить свет в кольцо Мёбиуса. В научном опыте ученые использовали оптические линзы, и структурированный свет — сфокусированный лазерный луч с преопределенными интенсивностью и поляризацией в каждой точке своего движения. В итоге были получены световые ленты Мебиуса.
Есть еще одна более масштабная теория. Вселенная – это огромная петля Мебиуса. Такой идеи придерживался Эйнштейн. Он предположил, что Вселенная замкнута, и космический корабль, стартовавший из определенной ее точки и летящий все время прямо, возвратится в ту же самую точку в пространстве и времени, с которой и началось его движение.
Пока это всего лишь гипотезы, у которых есть как сторонники, так и противники. Кто знает, к какому открытию подведет ученых, казалось бы, такой простой объект, как Лента Мебиуса.
Источник: kalkpro.ru
Эксперименты с листом Мёбиуса
Вначале изготовим лист Мёбиуса. Берем бумажную ленту АВСD. Прикладываем ее концы АD и СB друг к другу и склеиваем. Но не как попало, а так, чтобы точка А совпала с точкой С, а точка B с точкой D. Изготовим также обычное бумажное кольцо, края которого склеены обычным способом.
Чтобы понять, в чём особенность и отличие листа Мёбиуса, эксперименты будем проводить одновременно с обычным и перекрученным кольцом.


Эксперимент 1.
Определение непрерывности листа Мёбиуса.
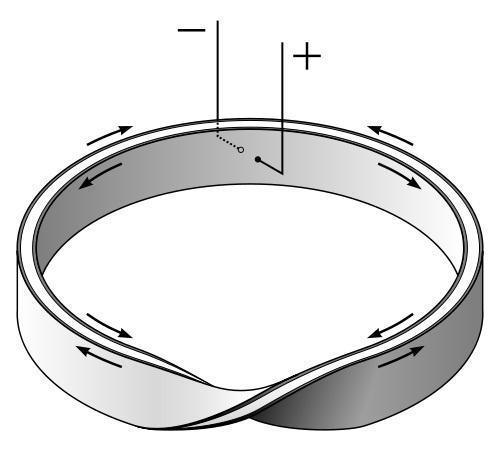
Поставим точку на одной стороне каждого кольца и проведём непрерывную линию вдоль него, пока не придём снова в отмеченную точку.
На обычном бумажном кольце линия проходит по одной стороне, замыкаясь в точке начала. В случае с листом Мёбиуса линия замыкается, полностью закрасив всю ленту. Следовательно, лист Мёбиуса – непрерывная поверхность. На листе Мёбиуса любая точка может быть соединена с любой другой точкой и при этом ни разу не придётся «переползать» через край ленты.
Эксперимент 2.
Определим, сколько сторон имеет лист Мёбиуса.
Попробуем закрасить краской обычное кольцо и лист Мёбиуса.
У обычного кольца закрашена только одна внешняя сторона. Внутренняя сторона осталась чистой. Лента Мёбиуса оказалась закрашена полностью.
«Внешняя» и «внутренняя» стороны в процессе закрашивания по ходу движения вдоль ленты как бы переходят друг в друга. Следовательно, у листа Мёбиуса только одна сторона! В книге «Что такое математика?» Рихард Курант и Герберт Робинс пишут: «Если кто-нибудь вздумает раскрасить только одну сторону поверхности мёбиусовой ленты, пусть сразу погрузит её всю в ведро с краской».


Эксперимент 3.
Определение, сколько краёв имеет лист Мёбиуса.
Закрасим непрерывной линией только один край колец.
В результате эксперимента мы обнаружили, что один край обычного кольца закрашен, второй край нет. Линия края ленты Мёбиуса оказалась, непрерывно закрашена на всём кольце.
Значит, у листа Мёбиуса не только одна сторона, но и только один край!


Эксперимент 4.
Разрежем кольца вдоль пополам, по линии параллельной краям и равноудалённой от краёв ленты.
При разрезании обычного кольца получилось два кольца, точнее две половинки от исходного кольца. Каждое будет уже, но длина их будет такой же, как длина первоначального кольца.
При разрезании листа Мёбиуса получилось одно перекрученное дважды кольцо в виде восьмёрки. Его длина в два раза больше, чем у исходного листа Мёбиуса. Значит, при таком разрезании лист Мёбиуса утратил свойство непрерывности.



Эксперимент 5.
Разрежем кольцо вдоль, отступив от края на 1/3 ширины кольца.
При разрезании обычного кольца получились два кольца: одно уже, другое шире. При разрезании ленты Мёбиуса получились два перекрученные сцепленные между собой кольца. Кольцо меньшего диаметра более широкое будет тоже листом Мёбиуса. Второе кольцо большего диаметра более узкое.


Эксперимент 6.
Возьмём кольца — результаты эксперимента 4 и разрежем их пополам вдоль.
При разрезании колец, полученных из обычного кольца, снова получились простые кольца. Их ширина стала ещё уже. При разрезании колец, получившихся при разрезании листа Мёбиуса, снова получились два перекрученные восьмёркой сцепленные друг с другом кольца.
Следовательно, листу Мёбиуса присуща связность: при разрезании вдоль края он не распадается на отдельные части.


Нам показалось неудобным каждый раз склеивать бумажные кольца для экспериментов на разрезание. Мы придумали и изготовили наглядное пособие «Лист Мёбиуса», сшив между собой пять разноцветных застёжек-«молний». Теперь нет необходимости каждый раз разрезать данную импровизированную ленту Мёбиуса. Достаточно расстегнуть нужную «молнию».




Выводы:
Листу Мёбиуса присущи интересные свойства:
Ø Лист Мёбиуса можно получить из прямоугольника, где длина значительно больше ширины, т. е. из полоски бумаги, ленты.
Ø Лист Мёбиуса имеет одну сторону (поверхность). Это подтверждают результаты 1 и 2 экспериментов.
Ø Лист Мёбиуса имеет один край. Результат эксперимента 3.
Ø Если пустить по поверхности листа Мёбиуса движущиеся объекты (например, паука и муху), они будут двигаться бесконечно долго, т.е. поверхность непрерывна.
Ø Листу Мёбиуса присуща связность.
Ø Следовательно, можно сделать вывод, что лист Мёбиуса – односторонняя непрерывная связная неориентируемая поверхность с одним краем.
Ø Лист Мёбиуса, как и любая топологическая фигура, не меняет своих свойств, пока её не разрезают, не разрывают, или не склеивают его отдельные куски.
Ø Свойства листа Мёбиуса присущи ему как геометрической фигуре и не связаны с его положением в пространстве.
Источник: kozelrozel.jimdofree.com