Найти содержание серебра в сплаве если в 300 г сплава содержится 63 г серебра

Содержание

(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.

Задание 1 #846
Уровень задания: Равен ЕГЭ

Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?

Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда

(4 — x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,

(dfracx) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac(4 — x)) – объём кислоты в растворе, содержащем (40%) кислоты.

Так как в итоге кислоты оказалось (dfrac cdot 4 = 1,3) литра, то:

[dfracx + dfrac(4 — x) = 1,3,] откуда находим (x = 1,5) .

Чистое серебро в К31-11-3

Задание 2 #844
Уровень задания: Равен ЕГЭ

Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.

Пусть (x) грамм – масса второго газа, тогда

(x + 300) грамм – масса первого газа,

(dfrac(x + 300)) грамм – масса кислорода в первом газе,

(dfracx) грамм – масса кислорода во втором газе,

тогда масса кислорода в третьем газе составляет (dfrac(2x + 300)) грамм.

Так как третий газ возник в результате смешивания первого и второго, то:

[dfrac(x + 300) + dfracx = dfrac(2x + 300),] откуда находим (x = 600) . Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.

Задание 3 #843
Уровень задания: Равен ЕГЭ

Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%) . В итоге у него получилось 5 литров молока жирностью (4,6%) . Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?

Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда

(5 — x) литров молока жирностью (6%) было у Ивана,

(dfracx) – объём жира в молоке жирностью (2,5%) , (dfrac(5 — x)) – объём жира в молоке жирностью (6%) .

Так как в итоге жира оказалось (dfrac cdot 5 = 0,23) литра, то:

(dfracx + dfrac(5 — x) = 0,23) , откуда находим (x = 2) .

Задание 4 #841
Уровень задания: Равен ЕГЭ

В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?

Читайте также:

Монета серебряная дерево любви

Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100 (%) . До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.

Сколько серебра в регулировачных СП3-33.

После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac cdot 100% = 18,4%.]

Задание 5 #2133
Уровень задания: Равен ЕГЭ

Во сколько раз больше должен быть объём (5) -процентного раствора кислоты, чем объём (10) -процентного раствора той же кислоты, чтобы при смешивании получить (7) -процентный раствор?

Пусть объём (5) -процентного раствора кислоты равен (x) литров, а объём (10) -процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac) при условии [0,05x + 0,1y = 0,07(x + y) qquadLeftrightarrowqquad dfrac = dfrac = 1,5,,] таким образом, ответ: (1,5) .

Задание 6 #2134
Уровень задания: Равен ЕГЭ

Во сколько раз больше должен быть объём (20) -процентного раствора кислоты, чем объём (14) -процентного раствора той же кислоты, чтобы при смешивании получить (18) -процентный раствор?

Пусть объём (20) -процентного раствора кислоты равен (x) литров, а объём (14) -процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac) при условии [0,2x + 0,14y = 0,18(x + y) qquadLeftrightarrowqquad dfrac = 2,,] таким образом, ответ: (2) .

Задание 7 #2629
Уровень задания: Равен ЕГЭ

Смешав (25) -процентный и (95) -процентный растворы кислоты и добавив (20) кг чистой воды, получили (40) -процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30) -процентного раствора той же кислоты, то получили бы (50) -процентный раствор кислоты. Сколько килограммов (25) -процентного раствора использовали для получения смеси?

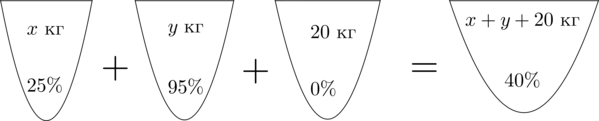
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfraccdot x) кислоты.

Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:

Аналогично составим схему, описывающую получение (50) -процентного раствора:

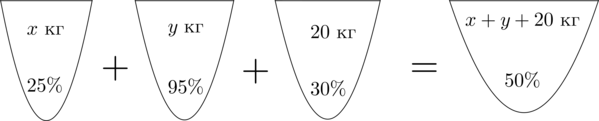
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:

Таким образом, решив систему из полученных двух уравнений, найдем (x) . Для этого можно умножить оба уравнения на (100) , чтобы сделать их проще на вид:

[begin 25x+95y+0=40(x+y+20)\ 25x+95y+30cdot 20=50(x+y+20) end]

Вычтем из второго уравнения первое и получим новую систему:

[begin begin 3x-11(40-x)+160=0\ y=40-x end quad Rightarrow quad begin x=20\y=20end end]

Таким образом, раствора с (25%) кислоты было (20) кг.

Источник: shkolkovo.net

Банк России выпустил памятную серебряную монету номиналом 3 рубля «Творчество Виктора Цоя»

Банк России радует поклонников рок-музыки и любителей коллекционирования монет новым выпуском памятной серебряной монеты, посвященной творчеству Виктора Цоя. Этот выдающийся советский рок-музыкант, солист и основатель легендарной группы «Кино» оставил незабываемый след в истории музыки и стал символом эпохи перестройки.

Монета номиналом 3 рубля изготовлена из серебра (чистота 925) и имеет форму круга диаметром 39,0 мм. Ее масса в чистоте составляет 31,1 г. Монета имеет выступающий кант, придающий ей дополнительный объемный эффект.

Читайте также:

Полироль для серебряной машины

На лицевой стороне монеты изображен рельефный Государственный герб Российской Федерации, а также надписи «РОССИЙСКАЯ ФЕДЕРАЦИЯ», «БАНК РОССИИ», номинал монеты «3 РУБЛЯ», дата «2023 г.», обозначение металла и пробы сплава. Кроме того, присутствует товарный знак Санкт-Петербургского монетного двора и указание массы драгоценного металла в чистоте.

Оборотная сторона монеты украшена рельефным изображением портрета Виктора Цоя с микрофоном на фоне гитары с символическими языками пламени. Слева по окружности нанесена рельефная надпись «ВИКТОР ЦОЙ», а внизу в две строки указаны даты жизни музыканта: «1962» и «1990». Боковая поверхность монеты имеет рифленую текстуру.

Монета выполнена в качестве «пруф», что означает ее высокое качество и отличную отделку. Всего будет выпущено 5 тысяч экземпляров этой памятной серебряной монеты.

Статус законного средства наличного платежа делает эту монету не только ценным коллекционным предметом, но и полноценным платежным средством на территории Российской Федерации. Она обязательна к приему по номиналу во все виды платежей без ограничений.

Источник: ЦБ РФ

Автор: Кирилл

В Нижнем Тагиле

В Каменске

В Первоуральске

В Арамиле

В Шале

Сообщить новость

Отправьте свою новость в редакцию, расскажите о проблеме или подкиньте тему для публикации. Сюда же загружайте ваше видео и фото.

8 800 300 43 25
Нашли ошибку в тексте?
Выделите её мышкой и нажмите

1. Все отзывы, оставленные посетителями сайта, поступают в редакцию и прочитываются людьми, имеющими непосредственное отношение к выходу статьи: журналистом, редактором, модератором.
2. Отзывы прочитываются людьми, имеющими непосредственное отношение к выходу статьи: журналистом, редактором, модератором. Отзывы выставляются на сайт с 07:00 до 22:00 в будние дни и с 09:00 до 18:00 в выходные и праздничные (время московское). Если по прошествии разумного времени отзыв не появился на сайте, то это могло быть вызвано следующими причинами:

— ваш комментарий носил критичный или провокационный характер о работе редакции данного сайта. Действия администрации сайта в комментариях не обсуждаются
— ваш отзыв носил провокационный характер: призывы к межнациональной и социальной розни, к свержению действующей власти и т. п.;
— ваш отзыв содержал нецензурную брань, в т.ч. в криптованном виде, т.е. с заменой букв на символы либо заменой брани на слово с аналогичной фоносемантикой;
— ваш отзыв содержал выражения оскорбительного характера в чей-либо адрес: автора материала, лиц, давших свои комментарии к статье, в адрес героя и т. д. Также не выставляются отзывы, в категоричной форме и бездоказательно — обвиняющие вышеуказанные лица в некомпетентности либо угрожающие им судебным преследованием – в таких случаях вам следует обращаться в прокуратуру напрямую;
— ваш отзыв содержал прямую рекламу (название и контактную информацию) фирмы, речь о которой не шла в авторском материале;
— ваш отзыв указывал на грамматические и орфографические ошибки ранее высказавшихся: грамотность – личное дело каждого;
— ваш отзыв содержал вопрос, ответ на который был дан ранее;
— ваш отзыв содержал слова из молитвы какой-либо религии (например: Аминь) или носит религиозный характер;
— ваш отзыв состоял из одного-двух слов, не несущих информативной нагрузки: «Афтар жжет», «Супер», «Наконец-то», «Отстой». Если цель вашего отзыва – дать односложную оценку мнению кого-либо из высказавшихся, воспользуйтесь рейтингом: «+», если вы поддерживаете комментатора, и «-», если не поддерживаете;
— ваш отзыв содержал слишком длинную ссылку или конструкцию, написанную без пробелов («плохие__________водители___________» и т. п.).

Читайте также:

Карась серебряный вес длина

Источник: ural24.com

Задачи на сплавы и смеси на ЕГЭ 2023 с решением

Zadachi na smesi i splavy

Как правило, ученики очень не любят задачи на сплавы и смеси. Для них они являются сложными и непонятными.

Поэтому многие даже время не тратят на попытки решения такой задачи в ЕГЭ, а просто пропускают ее. А зря!

Сейчас покажем, как можно решить такую задачу, выполнив всего три действия.

Как решить задачу на смеси и сплавы: 3 действия
Примеры решения задач на смеси: от простого к сложному
Примеры решения задач на сплавы: от простого к сложному

Как решить задачу на смеси и сплавы: 3 действия

Итак, решение любой задачи на смеси и сплавы сводится к выполнению трех действий:

Необходимо составить таблицу, в которой указываем общую массу каждого вещества и чистую массу каждого вещества. Эти данные содержатся в условии задачи. Если какие-то данные в условии отсутствуют, то обозначаем их как неизвестные — х, у.
Составляем систему уравнений, основываясь на том, что при соединении двух смесей (или сплавов) их массы складываются. Т.е. мы складываем как общую массу двух изначальных смесей (или сплавов), так и чистую массу каждого вещества, содержащихся в них. Решаем полученную систему уравнений.
После решения системы уравнений и нахождения всех неизвестных обязательно возвращаемся к условию задачи и смотрим, что требовалось найти. Многие ученики, решив правильно систему уравнений, неправильно записывают ответ. Ведь решение системы – это еще не ответ к задаче! Вернитесь к условиям задачи, прочитайте, что именно требовалось найти, и запишите ответ.

Примеры решения задач на смеси: от простого к сложному

А теперь разберем на примерах, как с помощью этих трех действий решать задачи на смеси и сплавы.

Задача 1

Смешали 3 литра раствора, содержащего 20% кислоты, и 5 литров раствора, содержащего 40% той же кислоты. Какова концентрация кислоты в полученном растворе.

Для решения задачи выполняем три действия, о которых мы говорили выше:

1. Составляем таблицу, в которой указываем общую массу раствора и массу чистого вещества, то есть в нашем случае – кислоты.

Из условий задачи имеем три раствора:

Раствор 1: 3 литра с 20% кислотой, т.е. общая масса = 3 литра, масса чистого вещества = 3 * 20% = 3 * 0,2 = 0,6

Раствор 2: 5 литров с 40% кислотой, т.е. общая масса = 5 литров, масса чистого вещества = 5 * 40% = 5 * 0,4 = 2

Zadachi na smesi i splavy

Раствор 3: какое-то количество раствора (обозначим его общую массу за х) с какой-то концентрацией кислоты (обозначим ее чистую массу за у), заносим эти данные в таблицу:Первое действие выполнено, переходим ко второму.

2. Составляем уравнения. Вспоминаем, что общая масса раствора 3 является суммой общих масс раствора 1 и раствора 2. А масса чистого вещества в растворе 3 является суммой массы чистового вещества в растворе 1 и массы чистового вещества в растворе 2. Таким образом, получаем:

Читайте также:

Звезды золотые или серебряные

Решаем простейшее уравнение и получаем, что х = 8, а у = 2,6. Таким образом, раствор 3 получился 8 литров, из которых 2,6 литра – это кислота.

Но ответ к задаче записывать рано! Переходим к третьему действию решения нашей задачи.

3. Возвращаемся к условию задачи и вспоминаем, а что же требовалось найти. В нашей задаче требовалось определить концентрацию кислоты в растворе 3. Когда мы решили уравнения, мы нашли общую массу раствора 3 и массу чистого вещества (кислоты), содержащегося в нем.

Чтобы определить концентрацию вещества необходимо разделить массу чистого вещества на общую массу раствора.

Таким образом, концентрация кислоты в растворе 3 равна:

Переводим долю вещества в проценты. Для этого умножаем полученный результат на 100:

Задача 2

Газ в сосуде А содержал 21% кислорода, а газ в сосуде В содержал 5% кислорода. Масса газа в сосуде А была больше массы газа в сосуде В на 300 г. Когда перегородку между сосудами убрали, газы перемешались, и получился третий газ, который содержит 14,6% кислорода. Найти массу третьего газа.

(х +300) * 0,21 + х * 0,05 = 0,146 (х + (х +300))

0,21х + 63 + 0,05х = 0,292х + 43,8

0,26х + 63 = 0,292х + 43,8

3. Возвращаемся к условиям задачи и вспоминаем, что нужно было найти. А найти нам нужно было массу третьего газа. Подставляем в уравнение общей массы газа 3 из таблицы и получаем:

600 + 600 + 300 = 1500 г

Ответ: масса третьего газа равна 1500 г.

Задача 3

Смешали 40%ый и 15%ый растворы кислоты, затем добавили 3 кг чистой воды, в результате чего получили 20%ый раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%ый раствор кислоты. Сколько килограммов 40%го и 15%го растворов кислоты было смешано?

1. Составляем таблицу. По условиям задачи мы имеем пять растворов:

Раствор 1: 40%ая кислота. Обозначим ее массу за х, тогда масса чистого вещества = х * 40% = 0,4х

Раствор 2: 15%ая кислота. Обозначим ее массу за у, тогда масса чистого вещества = х * 15% = 0,15х

Вода: вода, масса которой равна 3 кг. Концентрация кислоты в воде равна 0. Таким образом, масса чистого вещества равна 3 * 0 = 0

Раствор 3: 80%ая кислота. Ее масса по условию задачи равна 3 кг, тогда масса чистого вещества равна 3 * 80% = 3 *0,8 = 2,4

Раствор 4: соединение раствора 1, раствора 2 и воды. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 0

Раствор 5: соединение раствора 1, раствора 2 и раствора 3. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 2,4.

Zadachi na smesi i splavy 3

Сводим полученные результаты в таблицу:2. Составляем уравнение.

По условиям задачи раствор 5 имеет концентрацию 50%. Таким образом, чтобы получить массу чистого вещества в растворе 5 нужно его общую массу умножить на концентрацию. Получаем (х + у + 3) * 0,5. Теперь берем массу чистого вещества раствора 5, которую мы выразили в таблице и приравниваем два этих уравнения:

Читайте также:

Литр серебра сколько весит

(х + у + 3) * 0,5 = 0,4х + 0,15у + 2,4

Аналогично поступаем с раствором 4. По условиям задачи его концентрация равна 20%. Тогда получаем следующее уравнение:

(х + у + 3) * 0,2 = 0,4х + 0,15у

Zadachi na smesi i splavy 4

Объединяем полученные уравнения в систему:Решаем систему и получаем х = 3,4, у = 1,6

3. Возвращаемся к условиям задачи.

По условиям задачи необходимо было найти, какое количество килограммов 40%го и 15%го растворов кислоты было смешано. Общая масса 40%й кислоты мы обозначали х, а общую массу 15%й кислоты мы обозначили у. Следовательно, масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.

Ответ: масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.