Это статистическое уравнение, в котором неизвестное – только продольная составляющая скорости Vt. Можно провести усреднение по столкновениям, вводя частоту столкновений ν (число ударов в единицу времени) и средний косинус угла отклонения – эта характеристика реакции не сильно отличается от нуля. Обычно вводят эффективную частоту столкновений: νэфф =ν(1-θ>).
Надо сказать, что предположение о том, что частота столкновений не зависит от энергии электрона, также достаточно грубое приближение.
Получаем уравнение усредненного движения:
Будем называть далее усредненную продольную скорость дрейфовой скоростью Vd.
Подвижность.
Уравнение ( 7 ) интегрируется для случая однородного поля. Решение имеет вид ( 8 ):
Решение ( 8 ) демонстрирует, что средняя продольная компонента скорости Vd быстро устанавливается. Время установления составляет порядка 1/νэфф, то есть порядка времени между столкновениями. Стационарное значение дрейфовой скорости Vd равно:
Коэффициент пропорциональности μ между дрейфовой скоростью и напряженностью поля называется подвижностью.
КАКАЯ СКОРОСТЬ ТОКА В ПРОВОДАХ?
Итак, в рамках данной модели оказывается, что электрон перемещается вдоль поля с постоянной скоростью. Но это не означает, что в среднем возникает сила, аналогичная силе трения, которая не дает увеличиваться импульсу и поглощает энергию, передаваемую электрическим полем. Ведь мы сами заложили в модель тот факт, что в упругих столкновениях энергия не теряется. Противоречия здесь нет, столкновения останавливают рост средней скорости, но не среднеквадратичной.
Дрейфовая и тепловая скорости.
Дрейфовая скорость Vd определяет перемещение электрона в пространстве на масштабах много больше пробега между столкновениями. В каких случаях можно использовать эту величину?
Плотность электрического тока при движении набора частиц с зарядами qi и скоростями Vi в области пространства с объемом V равна:
При большом числе частиц в объеме с одинаковыми зарядами происходит усреднение вектора скорости. Таким образом, с электрическим током связана именно усредненная скорость V>, то есть дрейфовая скорость.
С другой стороны, способность электрона ионизовать или возбудить молекулу, зависит от его кинетической энергии. Средняя кинетическая энергия определяется среднеквадратичной скоростью V 2 >. Назовем эту величину тепловой скоростью Vth:
Именно через нее выражается средняя кинетическая энергия электронов:
Полный путь и путь по дрейфу.
Дрейфовая скорость позволяет вычислять перемещение электрона за много упругих ударов. Выше было показано, что вне зависимости от начальной скорости через несколько упругих ударов электрон в среднем начинает двигаться вдоль силовой линии. Значит, на больших масштабах мы можем считать, что электрон двигается вдоль силовой линии. Силовая линия поля представляет усредненную гладкую траекторию движения электрона в воздухе. Длина участка силовой линии, которую прошел электрон, называют путь по дрейфу.
Движение свободных электронов в металлах
Однако реальная траектория электрона оказывается хаотичной, а значит, более протяженной. Длина реальной траектории электрона называется полный путь.
Дрейфовая скорость дает нам перемещение электрона вдоль силовой линии на больших пространственных масштабах, а значит, связана с путем по дрейфу sd:
Тепловая скорость связана с полным путем sполн:
Источник: vunivere.ru
Расчет тепловой скорости движения электронов
Свободные электроны в металле образуют электронный газ. Рассчитаем скорость беспорядочного движения электронов в газе V, предполагая, что они подчиняются обычным газовым законам. Тогда кинетическая энергия движения электронов равна
(18)
где me– масса электрона,
Эта энергия равна энергии теплового движения, которая определяется абсолютной температурой газа T
(19)
где k– постоянная Больцмана.
Приравнивая (17) и (18) находим
(20)
Подставив значения для комнатной температуры t= 20 o C и справочные данныеk= 1,38*10 -23 Дж/К ,me= 9*10 -31 кг получим
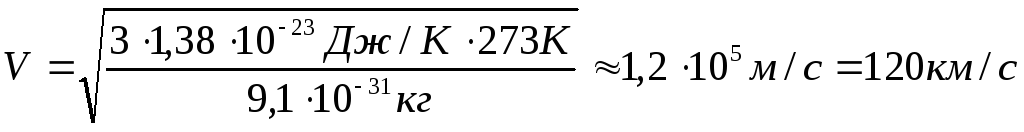
Полученную скорость называют тепловой скоростью электронов Vтепл.
Задачи для самостоятельного решения
- Рассчитать скорость теплового движения электронов в проводнике электронагревательной спирали из нихрома при температуре 600 о С по модели электронного газа.
- Рассчитать скорость теплового движения электронов в медном проводнике, охлажденом до температуры жидкого азота –195 о С.
Расчет электрической проводимости металлов
Запишем закон Ома 
(21) Подставим в него выражение для сопротивления проводника 
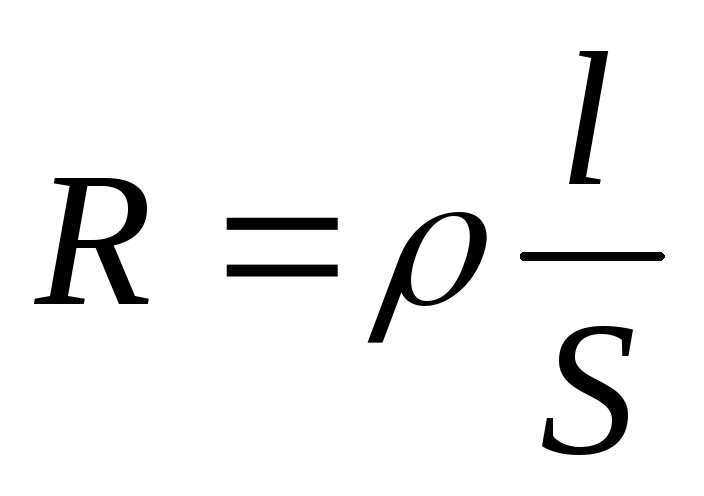(22) где l– длина проводника,S– его сечение ,– удельное сопротивление материала. Тогда 
или 
(24) Учтя , что I / S = jесть плотность тока,U / l = Eнапряженность электрического поля,1/ = удельная проводимость, получим закон Ома в локальной формулировке 
(25) Удельная проводимостьявляется свойством материала, которое, в свою очередь, зависит от характеристик движения электронов в металле.
Найдем эти соотношения. Так как 
(26) из (25) и (26) получим 
(27) Обозначим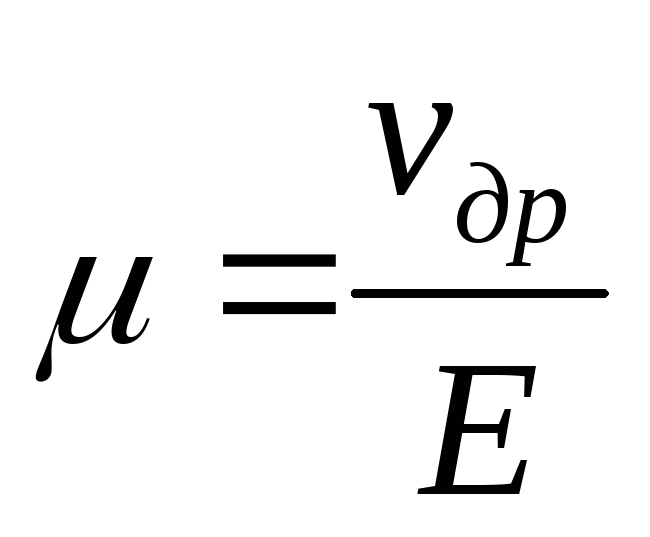 
(28) Величина называется подвижностью носителей заряда.
Тогда 
(29) Для расчета дрейфовой скорости электронов vдрвоспользуемся моделью свободного движения электронов в промежутках между столкновениями с ионами кристаллической решетки. Среднее время свободного движения называется временем релаксациирел, расстояниепреодолеваемое электроном за это время – длиной свободного пробега. Они связаны соотношением 
(30) За время движения между столкновениями, за счет действия силы со стороны электрического поля, электрон приобретает импульс p 
(32) Приравнивая его к (31) находим 
(33) Подставим полученное выражение в (27) , получим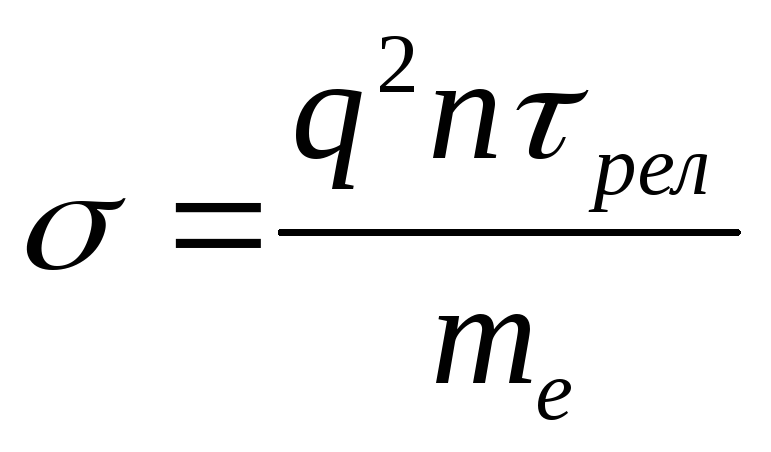 
(34) или, учтя (30), 
(35) В данную формулу входит неизвестная величина длины свободного пробега . В качестве приблизительной оценки выберем ее равной десяти периодам кристаллической решетки металла.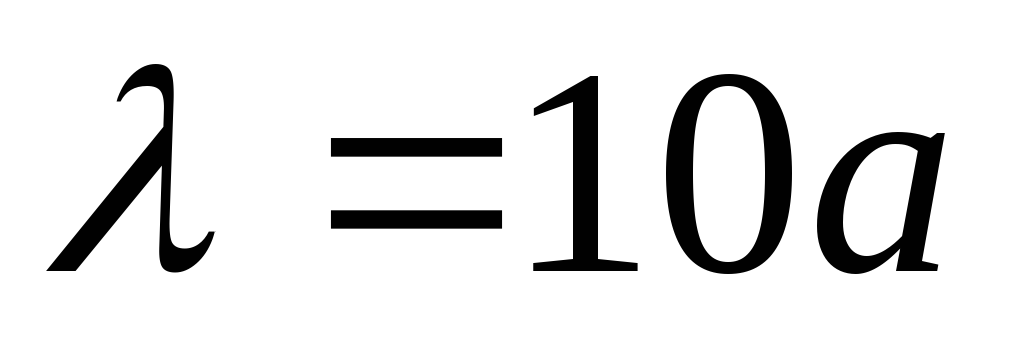 
Тогда подставив другие известные величины, получим, например, для меди величину удельной электрической проводимости 
или для удельного электрического сопротивления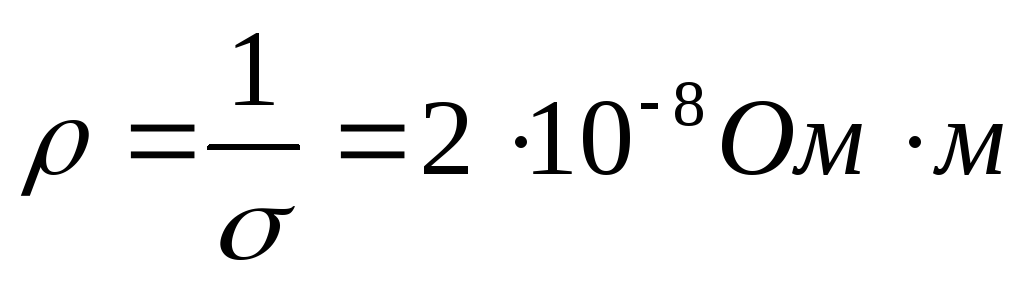 
Сравнивая полученную величину с табличным значением 
, видим хорошее согласие с экспериментальными данными.
Задачи для самостоятельного решения
- Как изменяется длина свободного пробега электронов в металлическом проводнике при его нагревании?
- Во сколько раз изменится длина свободного пробега электронов при нагревании серебряного проводника от 300 до 1000 К?
- Почему удельное электрическое сопротивление ферромагнитных металлов существенно выше неферромагнитных?
- Рассчитать электропроводность медного проводника, приняв длину свободного пробега электронов в металле равной 5 нм.
- Рассчитать электропроводность проводника из никеля, приняв длину свободного пробега электронов в металле равной 2 нм.
Источник: studfile.net
Доррга. Лабораторная работа 2 ИЗМЕРЕНИЕ ЗАРЯДА И ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА лабораторная работа 3
Единственный в мире Музей Смайликов
Самая яркая достопримечательность Крыма
Скачать 0.84 Mb.
Порядок выполнения эксперимента
35
Задание 1 Снятие вольтамперной характеристики и определение удельного сопротивления проводника.
1. На миниблоке «Удельное сопротивление» установите с помощью отвёртки заданную длину проводника от 0,5 до 2,5 м.
2. Установите миниблок на наборную панель и запишите значения длины проводника, диаметра:
=
l
……………….м;
=
d
…………….мм;
3. Соберите цепь как показано на рис.5, используя правый мультиметр в качестве вольтметра, а левый — в качестве амперметра. Установите на них соответствующие режимы и пределы измерения 20 В и 200 мА.
4. Включите блок генераторов напряжений и установите регулятором ток в цепи 50 мА. Запишите в табл.1 значения тока и напряжения.
5. Изменяя ток от 50 до 150 мА через 10 мА, запишите в таблицу значения тока и напряжения.
Рис. 5
36 6. Построить вольт-амперную характеристику, т.е. зависимость
( )
U
f
I
=
7. Вычислить сопротивление
R
по формуле
I
U
R
∆
∆
=
8. Определите удельное сопротивление материала, из которого изготовлен проводник: м
Ом
4 2
⋅
=
=
l
d
R
π
ρ
Таблица 1
№ п/п
U, B
I, мA
R, Ом
1 50 2
…
Задание 2 Определение температурного коэффициента сопротивления проводника
1. Установите миниблоки
«Температурная зависимость» и
«Электронный ключ» на наборное поле, как показано на рис. 6. и выполнить показанные на рисунке соединения.
Рис. 6 2. Включите компьютер и вызовите на дисплей виртуальный прибор:
«Термометр/термостат». Запишите в табл. 2 значение температуры и сопротивления проводника в исходном состоянии (без подогрева).
37 3. Включите термостат, введите в окно «Заданное значение температуры» какое-нибудь значение, превышающее температуру окружающей среды, включите блок генераторов напряжений и выведите регулятор напряжения в крайнее правое положение
(максимальный ток нагрева). При этом на термостате включится надпись «Нагрев», а в окне миниблока загорится сигнальная лампочка.
4. Следите за изменением температуры по красному столбику термометра. Как только температура превысит заданное значение на
C
0 5
,
1 1K
, нагрев выключится. После снижения температуры до значения на
C
0 5
,
1 1K
меньше заданного нагрев включится снова.
5. При отключенном нагреве измерьте сопротивления проводника (
R
) и запишите их значения в табл.2. (При включённом нагреве в участок цепи, на котором измеряется сопротивление, входит отрезок провода и контактное соединение, обтекаемые током нагрева, поэтому показание прибора будет неточным).
6. Шаг за шагом увеличивайте значение заданной температуры и, когда она достигается, измеряйте сопротивления проводника и записывайте их значения в таблицу.
Таблица 2 t, 0C
30 35
…
…
70
R, Ом
Предупреждения:
1. Для надёжной длительной работы миниблока не нагревайте его
выше
C
0 90
2. Ток нагрева в крайнем правом положении регулятора несколько
превышает номинальное значение тока генератора 200 мА, поэтому
возможно отключение генератора защитой, особенно при высокой
температуре окружающей среды. В этом случае нужно уменьшить ток
нагрева.
7. Постройте график зависимости сопротивления от температуры
( )
t
R
8. Определите температурный коэффициент сопротивления проводника. Для этого определите из графика значение сопротивления
R
при
=
t
(рис. 7) и коэффициент наклона прямой
t
R
∆
∆
. Тогда: град.
/
1 0
=
∆
∆
=
t
R
R
α
38
Контрольные вопросы.
1. Назовите условия появления и существования электрического тока.
2. Сформулируйте основные положения классической теории электропроводности металлов.
3. Опишите основные опыты, доказывающие, что носителями заряда в металлах являются электроны.
4. Оцените порядок дрейфовой скорости движения электронов и скорости их теплового движения. Какая из них больше?
5. Получите закон Ома в дифференциальной форме исходя из основных положений классической теории электропроводности металлов.
6. Какой вид имеет зависимость сопротивления металлов от температуры.
7. Сформулируйте физический смысл температурного коэффициента сопротивления.
8. Объясните, почему при включении электрической лампочки сила тока в ней в первый момент больше, чем после того, как лампочка начнет светиться?
Рис. 7
Источник: topuch.com