Откуда появились треугольники

Ученик в работе показал насколько интересена тема «Треугольник». Данную работу можно использовать на уроках геометрии в 7 — 9 классах.

Скачать:

Предварительный просмотр:

VIII межрегиональные соревнования школьников «Шаг в будущее, Юниор»

Этот удивительный треугольник.

Авторы: Ипаев Андрей.

Россия, Республика Бурятия, Муйский район,

п. Таксимо, 8 «А» класс

Научный руководитель: Панченко Галина Константиновна.

Россия, Республика Бурятия, Муйский район,

п. Таксимо, учитель математики МОУ СОШ №3

Оглавление .

1).Введение Стр. 2

2) Все о замечательном треугольнике. Стр. 2-3

3). Где используются треугольники. Стр.3-9

4). Всё треугольниками.

5) головоломки. Стр.9-14

Цель : Изучить историю создания треугольника и его применения в . жизни.

Задачи: 1)Изучить литературу по данному вопросу.

2)Рассмотреть логические задачи.

3)Исследовать, как с помощью треугольника можно составить

Краткая история Бермудского треугольника

4)Предложить игру «Треугольник в треугольнике»

1) Введение.

В 7 классе мы начали изучать геометрию. Эта удивительная наука покорила меня. Я захотел знать больше, чем изучают в школе. Учитель на уроке часто говорит о практической направленности математики. Мне захотелось понять, когда и где появились треугольники, кто и как их изобрёл, для чего они нужны, раскрыть особенности этой фигуры.

2) Все о замечательном треугольнике

Крупнейший древнегреческий историк Геродот (v век до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. По Геродоту, с этого и началась геометрия – «землемерие» ( от греческого «гео» — «земля» и «метрео» — измеряю ).

Древнее землемеры выполняли геометрические построения, измеряли длины и площади; астрологии рассчитывали расположение небесных светил – всё это требовало весьма обширных познаний о свойствах плоских и пространственных

Фигур, и в первую очередь о треугольнике.

Треугольник по праву считается простейшей из фигур: любая плоская, то есть простирающаяся в двух измерениях, фигура должна содержать хотя бы три точки ,не лежащие на одной прямой. Если соединить эти точки попарно прямолинейными отрезками, то построенная фигура и будет треугольником. Так же называют и заключенную внутри образовавшегося контура часть плоскости. Таким образом, любой плоскостной многоугольник может быть разбит на треугольники.

Изображение треугольников и задачи на треугольники встречаются в папирусах в документах. В древней Греции учение о треугольниках развивалось в ионийской школе Пифагора и других; оно было, затем полностью изложено в первой книге «Начал» Евклида.

Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.

Несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о «геометрии треугольника» как о самостоятельном разделе элементарной геометрии.

Выживший летчик рассказал, что он увидел в Бермудском треугольнике

При определении вида треугольника учитывают величины его углов и наличие равных сторон. По первому из этих признаков треугольники делят на остроугольные – у них все углы острые, прямоугольные – с прямым углом и тупоугольные – с тупым углом. У любого треугольника сумма углов равна 180 градусов, а потому только один из его углов не может быть острым. Стороны прямоугольного треугольника имеют особые названия: сторона, лежащая напротив прямого угла, называется гипотенузой, а две другие катетами. По наличию равных сторон различают три вида треугольников.

У равносторонних (или правильных) треугольников все три стороны равны. Равнобедренные треугольники имеют две равные стороны; эти стороны называют боковые, а третью основанием. Все остальные треугольники разносторонние. Равносторонние треугольники, по существу, все одинаковы – они имеют одну и ту же форму и могут отличаться лишь размерами.

Равнобедренные треугольники оказываются той очень удобной ступенькой, на которую нетрудно подняться, как только, только приступают к изучению геометрии. А с этой ступеньки уже открывается возможность дальнейшего движения вперёд.

В древней Греции учение о треугольниках развивалось в ионийской школе, основанной в VII в.до н.э. Фалесом, и в школе Пифагора. Уже Фалес доказал, что треугольник определяется одной стороной и двумя прилежащими к ней углами. Учение о треугольниках было затем полностью изложено в первой книге «Начал» Евклида.

Среди «определений», которыми начинается эта книга, имеются и следующие: «из трёхсторонних фигур равносторонний треугольник есть фигура, имеющая три равные стороны. Равнобедренный треугольник – имеющая только две равные стороны, разносторонний – имеющая три неравные стороны». Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.

О равнобедренном треугольнике. Фалес Милетский.

Равнобедренный треугольник обладает рядом геометрических свойств, которые привлекли к себе внимание ещё в древности. В задачах на треугольники, содержащихся в папирусе Ахмеда, на первый план выступают равнобедренный и прямоугольный треугольники. На практике часто применялось свойство медианы равнобедренного треугольника, являющейся одновременно и высотой и биссектрисой. Термин «медиана» происходит от латинского слова mediana – «средняя» (линия). То, что углы при основании равнобедренного треугольника равны, было известно ещё древним вавилонянам 4000 лет назад.

В четвертой книге «Начал» Евклид решает задачу: «Вписать круг в данный треугольник». Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга. Из решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре описанного круга.

3). Где в жизни встречаются треугольники?

Треугольник самая распространенная фигура. В лесу, когда мы смотрим на ель и ее тень, то перед нами представляется равнобедренный треугольник.

На магических символах.

Предметы обихода: треуголки, вырезы на одежде.

ТРЕУГОЛЬНИК, самозвучащий музыкальный инструмент — стальной прут, согнутый в виде треугольника, по которому ударяют палочкой. Применяется в оркестрах и инструментальных ансамблях.

Среди бесконечного количества возможных прямоугольных треугольников, особый интерес всегда вызывали так называемые «пифагоровы треугольники», стороны которых являются целыми числами. Несомненно, «пифагоровы треугольники» также относятся к разряду «сокровищ геометрии», а поиски таких треугольников представляют одну из из интереснейших страниц в истории математики. Наиболее широко известным из них является прямоугольный треугольник со сторонами 4, 3 и 5. Он назывался также «священным» или «египетским», так как он широко использовался в египетской культуре

3)Аномальные явления в природе связанные с геометрией треугольника.

Почему пишут о бермудском треугольнике, а не, скажем, о Багамским, Флоринском или пуэрто-риканском? Почему говорят о треугольнике, а не, к примеру, о квадрате, круге или трапеции? Бермудский треугольник — далеко не единственное название этого удивительного района в западной части Атлантического океана. Его называют также «дьявольское море», «кладбище Антлантики», «море вуду», «море проклятых». И все-таки почему, собственно, бермудский? Ведь

Бермудские острова образуют лишь одну из вершин этого треугольника и расположены отнюдь не в его центре. Вероятно, определение «бермудский» укоренилось по той причине, что многие загадочные исчезновения случились именно около Бермуд, а может быть, потому, что слово это довольно выразительно и благозвучно. Так что название «бермудский треугольник» вошло в обиход, скорее всего, из-за своих фонетических достоинств. Все утверждают, что в бермудском треугольнике происходят сверхъестественные, необъяснимые вещи. Это место, между Флоридой, Кубой и Бермудами, считается самым ужасным, самым жутким местом планеты.

В 5 декабря 1945 года было обычным днем для американских ВВС, базирующихся во Флориде. В то время на службе там состояло большое количество пилотов, получивших богатый боевой летный опыт, поэтому происшествия в воздухе случались сравнительно редко. Да и задание на этот раз они получили не слишком сложное: выйти прямым курсом на Чикен Шоал, находящийся севернее острова Бимини.

Погода была великолепной, пять трехместных бомбардировщиков-торпедоносцев «Эвенджер» («Мстители») взлетели и взяли курс на восток, имея на борту горючего на 5,5 часов.

Больше их никто не видел, что было с ними потом — ведает лишь один Бог. Различных гипотез (чаще всего надуманных) и версий по этому поводу было выдвинуто предостаточно. Все они оставались недосказанными только лишь по одной причине — не были найдены пропавшие самолеты.

После дела о пропаже 5 самолетов «как грибы после дождя» стали возникать новые истории с печальным концом. «Обычных» таинственных исчезновений бермудологам было уже недостаточно, поэтому в ход пошли приписки, недомолвки и просто обман, в результате которых в число жертв треугольника попали суда, утонувшие либо по вполне тривиальным .

Настоящих, запротоколированных случаев исчезновений кораблей едва ли наберется больше 10-15% оттого, что сообщалось в сенсационных газетных публикациях. Вся беда в том, что

разобраться с этими случаями практически невозможно, это таинственное «нечто» не оставляет свидетелей.

Итак, первый и бесспорный вывод, который следует из прослушивания радиопереговорных записей — пилоты столкнулись в воздухе с чем-то необычным и странным. Океан имеет странный вид, появилась «белая вода», стрелки приборов пляшут. Да и в самом Бермудском треугольнике «белый туман» не такой уж редкий гость. После встречи с ним исчез однажды с экранов локаторов приближавшийся к Майами авиалайнер, и когда через 10 минут появился вновь, все имевшиеся на борту часы отставали на те же самые минуты. В том полете никто из пассажиров ничего необычного не заметил; не исключено, что так же незаметно для глаз будет внезапное увеличение скорости по причине «фокусов» со Временем.

Что же говорить о районе Бермуд в Атлантике, где мощное течение Гольфстрим закручивает водяные вихри в сотни километров диаметром! (Именно подобные образования иногда становятся видимыми на поверхности океана в виде белых или даже слабосветящихся кругов и «колес»). Закручиваются вихри — изменяется Время — должна изменяться и гравитация.

В центре вихря (там, где американские спутники фиксировали уровень воды на 25-30 метров ниже обычного) гравитация повышенная, на периферии — пониженная. Не в том ли причина многих катастроф морских судов, что грузы в трюме внезапно увеличивают свой вес? При неоднородном нагружении и превышении запаса прочности корпуса катастрофа практически неминуема! Для полноты трагической картины к этому нужно добавить и ненадежность радиосвязи в таких местах.

Зато кое-какие выводы можно сделать в деле с пропажей 5 самолетов. Вероятнее всего, в небе над Бермудским треугольником это звено столкнулось с нестационарной кочующей аномальной зоной, в которой у них отказали приборы и забарахлила радиосвязь. Затем самолеты, находясь в «странном тумане», с очень большой скоростью переместились в Мексиканский залив, где пилоты и узнали с удивлением местную гряду островов.

Вот оно, недостающее звено в цепи разгадок! Пока на земле прошел всего один час, в белом тумане пролетело около трех!! Скорость самолетов была все это время обычной, но для гипотетического стороннего наблюдателя она показалась бы в 3 раза быстрее! Вероятно, за эти 3 часа собственного времени торпедоносцы, увы, проскочили выступ Флориды с родной базой и оказались в Мексиканском заливе. Пилоты еще до конца не вышли из цепких лап весьма поредевшего тумана, когда под крыльями появилась гряда островов.

Треугольники в астрономии .

Маленькое созвездие к юго-востоку от Андромеды. У его западной границы видна спиральная галактика М 33, или Туманность Треугольника (5,7 зв. вел.), повернутая к нам почти плашмя. Ее английское прозвище Pinwheel переводится как «цевочное колесо» – разновидность зубчатого колеса со стерженьками вместо зубьев; оно довольно точно передает видимую форму галактики.

Она, как и Туманность Андромеды (М 31), член Местной группы галактик. Обе они расположены симметрично относительно звезды Мирах ( Андромеды), что существенно

облегчает поиск более слабой М 33. Обе галактики находятся от нас примерно на одинаковом расстоянии, но Туманность Треугольника чуть дальше, на расстоянии 2,6 млн. световых лет.

4)Всё треугольниками.

Из треугольников можно составить разные: предметы, фигуры, вещи. В общем из треугольников можно составить всё.

Например, из треугольников можно составить планету земля.

Из треугольников можно составить сердце.

Можно составить солнце.

Источник: nsportal.ru

Треугольники

В повседневной жизни нас окружает масса предметов имеющих треугольную форму. Например: Часы, воздушный змей, кусочек торта, пиццы, арбуза, салатники, рамки для фотографий, пузырек парфюма – этот список можно продолжать бесконечно. Но что же такое треугольник?

План урока:

Как выглядит треугольник?

В выходной день Глеб с родителями ехали в парк. Мальчик заметил, что вдоль дороги стояла непонятная табличка, увидев которую, отец поехал очень медленно.

«Что это такое?» – поинтересовался ребенок. Папа рассказал, что это дорожный знак, который предупреждает о трудностях на пути. Глебу очень понравился знак, а особенно его форма. Отец продолжил рассказ о знаках: «Форма знака о многом говорит водителю, ведь при плохой видимости автолюбитель видит только форму, а не надпись.

Поэтому все предупреждающие знаки – треугольные». «А что такое треугольные?» – не унимался мальчик. Найти ответ на этот и многие другие вопросы папе помог наш сегодняшний урок.

Вначале, давайте разберемся, что же такое треугольник и из чего он состоит.

В повседневной жизни нас окружает масса предметов имеющих треугольную форму. Например:

Часы, воздушный змей, кусочек торта, пиццы, арбуза, салатники, рамки для фотографий, пузырек парфюма – этот список можно продолжать бесконечно. Но что же такое треугольник?

Приведем примеры треугольников:

Исходя из определения, каждый рисунок состоит из трех отрезков. В геометрии такие отрезки называют сторонами треугольника.

Кроме отрезков, составляющей частью фигуры являются три точки, которые принято называть вершинами.

В геометрии, вершины треугольника принято обозначать заглавными буквами латиницы: A,C,D,B.

Начертим треугольник. Вершины, обозначим буквами A,C,D.

Данная геометрическая фигура имеет три вершины A,C,D и три стороны АС, CD, DА.

А как же на письме показать, что данная фигура является треугольником?

Очень интересным является то, что записывать название, можно перечисляя вершины в любом порядке.

Можно записать: ∆NOK, ∆OKN, ∆KNО. Каждый вариант записи обозначает один и тот же треугольник и является верным.

Само название фигуры «Треугольник» предполагает, что в состав должны входить три угла. Так ли это?

Внимательно рассмотрим рисунок:

Действительно, мы видим три угла, которые отмечены дугами: ∠RFP,∠FPR, ∠PRF(мы уже знаем, что буква, обозначающая вершину угла всегда записывается в середине) или∠F, ∠P,∠R.

Виды треугольников

Все геометрические фигуры, имеющие треугольную форму,делятся на группы по двум направлениям:

• По углам.
• По сторонам.

Давайте рассмотрим, на какие группы делятся треугольники по углам:

Теперь, познакомимся с группами треугольников по сторонам(на рисунках равные стороны принято обозначать одинаковым количеством черточек):

Постарайтесь запомнить все виды треугольников, так как на протяжении всего учебного процесса, вам часто придется сталкиваться с выполнением заданий на данную тему.

Равенство треугольников

Случаются ситуации, когда точно известно, что два треугольника равны, а что же в таком случае можно сказать про углы и стороны таких треугольников?

Нам дано: ∆ABC = ∆A1B1C1. Равны ли соответствующие стороны и углы данных фигур?

По условию треугольники равны. Значит, применяем рассмотренное правило, которое говорит о том, что все соответствующие элементы фигуры равны между собой.

Если ∆ABC = ∆A1B1C1, то равны соответствующие стороны:

и соответствующие углы равны:

Геометрия интересна тем, что большинство её правил нуждаются в доказательствах. Такие правила называют теоремами.

Вместе с этим, имеются и самостоятельные правила, которые называют аксиомами геометрии.

Сегодня мы рассмотрим первую теорему с названием «Первый признак равенства треугольников», и проведем работу по сбору доказательств для данной теоремы.

Два треугольника – ∆OMN и ∆KLT. Известно, что две стороны треугольников и угол между ними равны.

Докажем, что ∆OMN=∆KLT.

Доказательство первого признака равенства треугольников:

Из условия нам известно, что соответствующие углы равны ∠M =∠L, следовательно, мы можем выполнить наложение двух треугольников так, чтобы вершина M совпадала с вершиной L.

Тогда, сторона OM наложится на сторону KL, а сторона MN на отрезок LT. По условию нам известно, что отрезки равны OM=KL, MN=LT, значит, при наложении они совпадут. Получается, что при наложении совпадает угол, и две стороны, следовательно, будут совпадать и оставшиеся стороны ON и KT, то есть ON = KT . Если при наложении совмещаются три стороны и одна вершина, значит, совместятся и две другие вершины KO и TN.

Выходит, что при совмещении совпадают все элементы ∆, а такие ∆ называются равными.

Презентация, доклад Из истории треугольников

Слайд 2
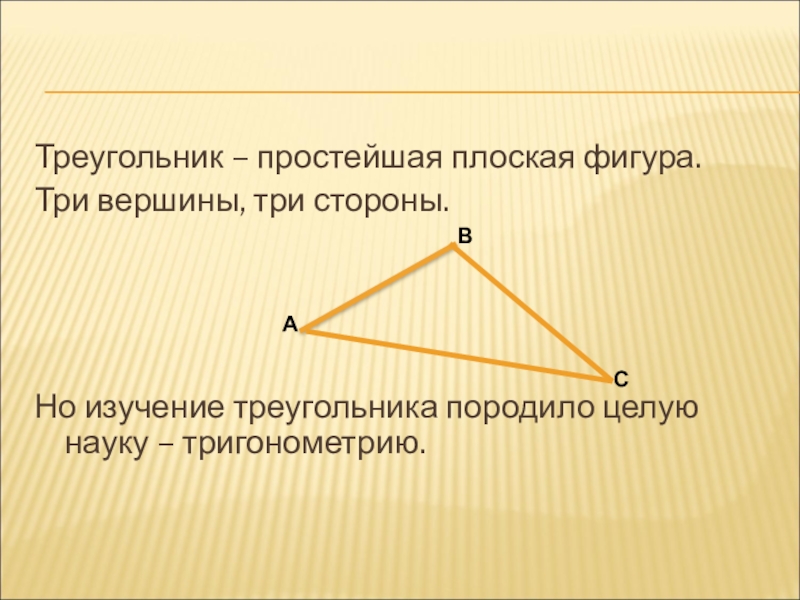
Треугольник – простейшая плоская фигура.
Три вершины, три стороны.

треугольника породило целую науку – тригонометрию.

Слайд 3ВАВИЛОН
Есть основания полагать, что именно они открыли то, что ныне известно

как теоремы о треугольниках.

В геометрии вавилоняне знали о таких соотношениях, как пропорциональность
соответствующих сторон подобных треугольников. Им известна теорема Пифагора.

Слайд 4ЕГИПЕТ
Первые упоминания о треугольнике и его свойствах ученые находят в египетских

папирусах, которым более 4000 лет.

Слайд 5ДРЕВНЯЯ ГРЕЦИЯ
В Древней Греции изучение свойств треугольника достигает высокого уровня –

это теорема Пифагора и формула Герона, которым более 2000 лет.

Пифагор и его последователи доказали много теорем о треугольниках.

Слайд 6ФАЛЕС МИЛЕТСКИЙ

Древнегреческий философ, математик, астроном.
Происходил из Милета (Малая Азия).
Образование

получил в Египте, там же занимался вычислением высот некоторых пирамид. Путешествовал по странам Востока. Произведения Фалеса не дошли до нашего времени, о них известно из сочинений его учеников и последователей.

Фалес первым доказал теорему о равенстве углов при основании равнобедренного треугольника, о равенстве двух треугольников по равным стороне и двум углам.

Слайд 7Тригонометрические функции возникли впервые в связи с исследованиями в астрономии и

геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся по существу тригонометрическими функциями, встречаются уже в 3 в. до н. э. в работах математиков Древней Греции — Евклида, Архимеда, Аполлония Пергского

Слайд 8 Слово тригонометрия впервые встречается в 1505 году в заглавии

книги немецкого математика Питискуса.
Тригонометрия – слово греческое и в переводе означает “треугольник”, “измеряю”.
В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них.
Возникновение тригонометрии
связано с землемерением,
астрономией и строительным
делом.

Слайд 9
В XV – XVI веках появилось огромное количество исследований свойств треугольника.

Это большой раздел планиметрии, получивший название “Новая геометрия треугольника”. Большой вклад в изучение свойств треугольника внес русский ученый Н.И.Лобачевский. Его труд «Новое начало геометрии» получил применение в физике, кибернетике и математике.

Слайд 10ПАСКАЛЬ БЛЕЗ
(Pascal Blaise) (1623-1662), французский религиозный мыслитель, математик и физик.

дар мальчика требовал проявления, и в 12 лет он самостоятельно, пользуясь собственным словарем и схемами, которые рисовал в комнате для игр, пришел к некоторым геометрическим выводам и пытался (не будучи знаком с Началами) построить доказательство 32-й теоремы первой книги Евклида: сумма углов треугольника равна сумме двух прямых углов.

Слайд 11ОБ ЭЛЕМЕНТАХ ТРЕУГОЛЬНИКА
Медиана (от латинского mediana — средняя) отрезок, соединяющий одну

из вершин треугольника с серединой противоположной стороны.

Слайд 12

Биссектриса (от лат. bis — дважды и seco — рассекаю) угла,

отрезок, выходящий из вершины угла и делящий его пополам

Слайд 13
ГИПОТЕНУЗА [греч. hypoteinusa — натягивающая] -сторона прямоугольного треугольника, лежащая против прямого

Слайд 14ТРЕУГОЛЬНИК-
Не только геометрическая фигура,

а и философское понятие…

Треугольник – триединая природа вселенной:

Слайд 15
НЕБО-ЗЕМЛЯ- ЧЕЛОВЕК
ОТЕЦ- МАТЬ-ДИТЯ

Слайд 16

У греков дельта символизирует дверь жизни, женское начало, плодородие.
У

пифагорейцев равносторонний треугольник символизирует Афину как богиню мудрости.

Источник: shareslide.ru