Опыт Штерна — опыт, впервые проведённый немецким физиком Отто Штерном в 1920 году. Опыт явился одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.
Для проведения опыта Штерном был подготовлен прибор, состоящий из двух цилиндров разного радиуса, ось которых совпадала и на ней располагалась платиновая проволока с нанесённым слоем серебра. В пространстве внутри цилиндров посредством непрерывной откачки воздуха поддерживалось достаточно низкое давление.
При пропускании электрического тока через проволоку достигалась температура плавления серебра, из-за чего атомы начинали испаряться и летели к внутренней поверхности малого цилиндра равномерно и прямолинейно со скоростью v, соответствующей подаваемому на концы нитинапряжению. Во внутреннем цилиндре была проделана узкая щель, через которую атомы могли беспрепятственно пролетать далее.
Как Вытянуть Металл
Стенки цилиндров специально охлаждались, что способствовало оседанию попадающих на них атомов. В таком состоянии на внутренней поверхности большого цилиндра образовывалась достаточно чёткая узкая полоса серебряного налёта, расположенная прямо напротив щели малого цилиндра. Затем всю систему начинали вращать с некой достаточно большойугловой скоростью ω. При этом полоса налёта смещалась в сторону, противоположную направлению вращения, и теряла чёткость. Измерив смещение s наиболее тёмной части полосы от её положения, когда система покоилась, Штерн определил время полёта, через которое нашёл скорость движения молекул:
,
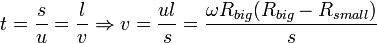
где s — смещение полосы, l — расстояние между цилиндрами, а u — скорость движения точек внешнего цилиндра.
Найденная таким образом скорость движения атомов серебра совпала со скоростью, рассчитанной по законам молекулярно-кинетической теории, а тот факт, что получившаяся полоска была размытой, свидетельствовал в пользу того, что скорости атомов различны и распределены по некоторому закону — закону распределения Максвелла: атомы, двигавшиеся быстрее, смещались относительно полосы, полученной в состоянии покоя, на меньшие расстояния, чем те, которые двигались медленнее.
8. Идеальный газ во внешнем силовом поле. Барометрическая формула.
Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.
Для идеального газа, имеющего постоянную температуру 
и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения 
одинаково), барометрическая формула имеет следующий вид: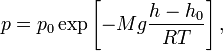 
Холодное цинкование жидким цинком (цинковый грунт, цинковая краска, цинковое покрытие)
где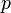 
— давление газа в слое, расположенном на высоте 
, 
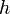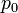— давление на нулевом уровне ( 
), 
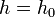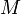— молярная масса газа, 
— газовая постоянная, — абсолютная температура. Из барометрической формулы следует, что концентрация молекул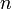 
(или плотность газа) убывает с высотой по тому же закону: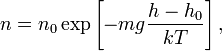 
где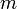 
— масса молекулы газа, 
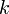— постоянная Больцмана.
Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина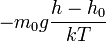 
, определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной 
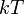. Чем выше температура , тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести 
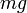(при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести может изменяться за счёт двух величин: ускорения и массы частиц .
Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.
Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.
Источник: studfile.net
10 класс
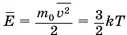
Из сопоставления основного уравнения MKT с уравнением состояния идеального газа ранее было получено выражение для средней кинетической энергии хаотического поступательного движения молекул идеального газа: . Из него можно найти средний квадрат скорости хаотического движения молекул:
В § 42 «Основное уравнение MKT» мы установили связь между этой величиной и среднеквадратичной скоростью. C учётом выражения (1) можно записать:
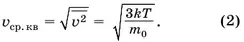
Так как постоянная Больцмана равна отношению универсальной газовой постоянной к постоянной Авогадро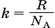 
, а массу молекулы можно выразить через её молярную массу 
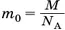, то из формулы (2) следует
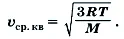
Вычисленные по этой формуле скорости для различных газов при t = 0 °C (Т = 273 К) приведены в таблице 3.
Таблица 3
| Газ | υср.кв, м/с |
| Водород | 1838 |
| Азот | 493 |
| Кислород | 461 |
| Углекислый газ | 393 |
Из неё видно, что скорости молекул имеют большие значения — порядка скорости артиллерийских снарядов — и несколько больше скорости звука в соответствующем газе. Если скорости молекул столь велики, то как объяснить, например, что запах духов, пролитых в комнате, распространяется довольно медленно; должно пройти несколько секунд, чтобы запах распространился по всей комнате.
Объяснить этот факт достаточно просто. Молекулы газа, несмотря на свои малые размеры, непрерывно сталкиваются друг с другом. Из-за большой скорости движения молекул число столкновений молекул воздуха в 1 с при нормальных атмосферных условиях достигает нескольких миллиардов. Траектория каждой молекулы представляет собой очень запутанную ломаную линию (рис. 6.25).
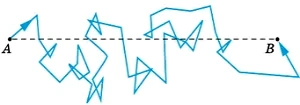
Молекула обладает большими скоростями на прямолинейных отрезках ломаной. Перемещение же молекулы в каком-либо направлении в среднем невелико даже за время порядка нескольких секунд. При перемещении молекулы из точки А в точку В пройденный путь оказывается гораздо больше расстояния AB (см. рис. 6.25).
Экспериментальное определение скоростей молекул газа.
Опыты по определению скорости теплового движения молекул подтвердили справедливость формулы (2).
Отто Штерн
Один из них был осуществлён немецким физиком Отто Штерном (1888—1969) в 1920 г. Одна из схем опыта Штерна показана на рисунке 6.26.
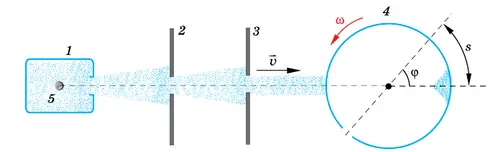
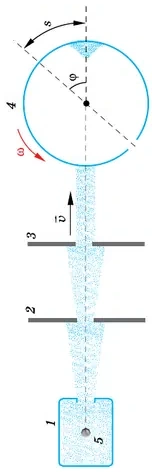
Прибор состоит из сосуда 1, системы диафрагм 2, 3 и цилиндра 4, вращающегося с большой угловой скоростью ω.
В сосуде 1 натянута тонкая платиновая проволочка 5, покрытая слоем серебра. По проволочке пропускают электрический ток. При прохождении тока слой серебра испаряется, и сосуд заполняется газом из одноатомных молекул серебра. Газ находится в равновесном состоянии при температуре Т, которую можно измерить.
В стенке сосуда 1 сделано маленькое отверстие, через которое небольшое количество молекул серебра вылетает из сосуда в пространство, где создан вакуум. Здесь молекулы практически не сталкиваются друг с другом. C помощью диафрагм 2, 3 выделяется пучок молекул, направленный вдоль диаметра вращающегося цилиндра. В цилиндре имеется узкая щель. В момент, когда щель оказывается на пути пучка, небольшая порция молекул попадает внутрь цилиндра и движется к его противоположной стенке.
Расстояние, равное диаметру цилиндра D, эти молекулы пролетают за время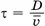 
, где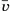 
— среднее значение скорости. За это время цилиндр повернётся на угол 
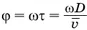Если бы цилиндр был неподвижен, то молекулы осаждались бы на его внутренней поверхности прямо напротив щели. Но при вращении цилиндра молекулы попадают на участок цилиндра, смещенный на расстояние 
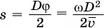от точки, лежащей на одном диаметре со щелью (см. рис. 6.26).
В результате на внутренней поверхности цилиндра образуется след от осаждённых молекул серебра в виде тёмного пятна. Его толщина не везде одинакова. Измерив длину дуги s, соответствующую наибольшей толщине слоя серебра, и зная диаметр цилиндра и его угловую скорость, можно определить среднюю скорость молекул по формуле
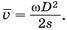
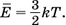
Полученные значения средней скорости молекул серебра находились в интервале 560—640 м/с, что соответствовало среднеквадратичной скорости, вычисленной по формуле (2) и равной 584 м/с. Это является экспериментальным доказательством справедливости формулы (2), а следовательно, и выражения Измеряя толщину пятна серебра в разных местах, можно приблизительно подсчитать число молекул, скорости которых лежат в тех или иных интервалах.
Анализ экспериментальных данных позволил найти распределение молекул газа по скоростям при определённой температуре. Видно, что построенная кривая (рис. 6.27) имеет максимум, показывающий, что наибольшее число молекул обладает скоростью υн.в.
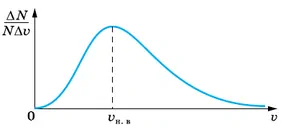
Наиболее вероятная скорость — это скорость, которой обладает максимальное число молекул.
Другими словами, модули скоростей большинства молекул близки к наиболее вероятной скорости. Наиболее вероятная и среднеквадратичная скорости отличаются друг от друга в пропорции υн.в : υср.кв ≈ 1 : 1,22.
Вопросы:
1. Опишите устройство экспериментальной установки Штерна.
2. Как было получено распределение молекул серебра по скоростям в опыте Штерна?
3. Какое значение имеет опыт Штерна для МКТ
Вопросы для обсуждения:
1. Скорости хаотического движения многих молекул при комнатной температуре близки к скорости летящей пули. Почему же запаху духов требуется заметное время, чтобы распространиться по комнате?
2. На высоте нескольких сотен километров над Землёй молекулы атмосферы обладают скоростями, которым соответствуют температуры в несколько тысяч градусов. Почему же не плавятся летающие на этой высоте искусственные спутники Земли?
3. Можно ли в опыте Штерна измерить скорость одной молекулы газа?
Пример решения задачи
В опыте Штерна покрытая серебром платиновая проволочка, натянутая вдоль общей оси цилиндров диаметрами 12 и 240 мм (рис. 6.28, a), нагрелась током.
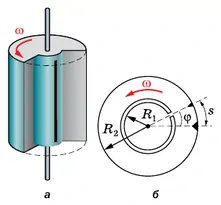
Испаряющиеся с её поверхности молекулы серебра пролетали в вакууме сквозь щель в малом цилиндре и создавали на поверхности большего цилиндра полоску серебра. Когда прибор приводился в быстрое вращение вокруг оси цилиндров, полоска смещалась на расстояние 7,6 мм (рис. 6.28, б). Вычислите среднюю скорость молекул, если температура нити равна 1173 К, а цилиндры совершают 2800 оборотов в минуту.
Ответ: ≈ 528 м/с.
Упражнения:
1. Каким будет смещение напылённой полоски серебра в приборе Штерна при частоте вращения 20 об/с, если скорость движения молекул 300 м/с? Радиус внешнего цилиндра 10 см. Радиусом внутреннего цилиндра пренебречь.
2. При вращении прибора Штерна (см. рис. 6.28) с частотой 45 об/с среднее смещение полоски серебра составляло 1,12 см. Радиусы внутреннего и внешнего цилиндра соответственно равны 1,2 и 16 см. Найдите скорость движения молекул серебра и оцените температуру нити.
Источник: xn—-7sbbfb7a7aej.xn--p1ai
Почему в опыте Штерна наблюдалось не только смещение, но и размытие полоски из атомов серебра?.
Задача №1. Почему в опыте Штерна наблюдалось не только смещение, но и размытие полоски из атомов серебра?
Решение:
Размытие полоски при конденсации атомов серебра на внутренней поверхности вращающегося цилиндра в опыте Штерна указывает на тот факт, что не все атомы серебра движутся с одинаковой скоростью. Встречаются очень «быстрые» атомы, скорости которых во много раз превосходят среднюю квадратичную скорость. Но есть и «медленные» атомы, скорость которых близка к нулю.
Задача №1. Почему в опыте Штерна наблюдалось не только смещение, но и размытие полоски из атомов серебра?
Задача №2. При вращении прибора Штерна с частотой 45 с-1 среднее смещение полоски серебра, обусловленное вращением, составляло 1,12 см. Радиусы внутреннего и внешнего цилиндров соответственно равны 1,2 и 16 см. Найти среднюю квадратичную скорость атомов серебра из данных опыта и сравнить ее с теоретическим значением, если температура накала платиновой нити равна 1500 К.
Задача №3. Какое количество вещества содержится в газе, если при давлении 200 кПа и температуре 240 К его объем равен 40 л?
Задача №4. Каково давление сжатого воздуха, находящегося в баллоне вместимостью 20 л при температуре 12 °С, если масса этого воздуха 2 кг?
Задача №5. В баллоне вместимостью 25 л находится смесь газов, состоящая из аргона (Аr) массой 20 г и гелия (Не) массой 2 г при температуре 301 К. Найти давление смеси газов на стенки сосуда.
Задача №6. Найти массу природного горючего газа объемом 64 м3, считая, что объем указан при нормальных условиях. Молярную массу природного горючего газа считать равной молярной массе метана (СН4).
Задача №7. Воздух объемом 1,45 м3, находящийся при температуре 20 °С и давлении 100 кПа, перевели в жидкое состояние. Какой объем займет жидкий воздух, если его плотность 861 кг/м3?
Задача №8. В одинаковых баллонах при одинаковой температуре находятся водород (Н2) и углекислый газ (СО2). Массы газов одинаковы. Какой из газов производит большее давление на стенки баллона и во сколько раз?
Задача №9. На рисунке 57 приведена изотерма для 1 моль газа при температуре 260 К. Построить на этом же чертеже изотермы: а) для 1 моль газа при 390 К; б) для 2 моль газа при 260 К.
Задача №10. В баллоне находится газ при температуре 15 °С. Во сколько раз уменьшится давление газа, если 40% его выйдет из баллона, а температура при этом понизится на 8 °С?
Рымкевич, А. П. Физика. Задачник. 1011 кл.: пособие для общеобразоват. Учреждений / А. П. Рымкевич. 10-е изд., стереотип. М.: Дрофа, 2006.
188, [4] с.: ил.
Источник: claw.ru