Предположив, что корона короля Гиерона в воздухе весит 20 Н, а в воде 18,75 Н, вычислите плотность вещества короны. Полагая, что к золоту было подмешано только серебро, обусловьте, сколько в короне было золота и сколько серебра. При решении задачки плотность золота считайте равной 20 000 кг/м3, плотность серебра 10 000 кг/м3. Каковой был бы объём короны из чистого золота?
- Toljan Lopatko
- Физика
- 2019-09-24 07:47:31
- 212
- 2
Антонина Михачева 2019-09-24 07:49:40
Рвозд = 20Н — вес короны в воздухе
Р вод = 18,75Н — вес короны в воде
вод = 1000 кг/м — плотность воды
g = 10 м/с — ускорение свободного падения
зол = 20 000кг/м — плотность золота
сер = 10 000кг/м — плотность серебра
m спл = Рвозд : g = 20 : 10 = 2(кг) — масса сплава
V cпл — ? — объём сплава
С одной стороны Fарх = Рвозд — Рвод , а с иной стороны по закону Архимеда Fарх = вод g Vспл, тогда
Vспл = (Рвозд — Рвод) : ( вод g) = (20 — 18,75) : (1000 10) = 1,2510(м)
Физика 7 класс, упражнение 26 номер 5
спл = m спл : V спл = 2 : 1,2510 = 16 000 (кг/м)
Для определения массы золота m зол и массы серебра m сер в сплаве cоставим два уравнения:
m зол + m сер = m cпл, откуда m зол = m спл — m cер (1)
V спл = m зол : зол + m cер : сер (2)
Подставим выражение (1) в (2)
V спл = (m спл — m cер) : зол + m cер : сер
V спл зол cер = (m спл — m cер) сер + m cер зол
V спл зол cер = m спл сер — m cер сер + m cер зол
m сер = сер (V спл зол — m спл) : ( зол — сер) =
= 10 000 (1,2510 20 000 — 2) : (20 000 — 10 000) = 0,5(кг)
m зол = m спл — m сер = 2 — 0,5 = 1,5(кг)
Найдём объём короны из незапятнанного золота, имеющей вес в воздухе Рвозд = 20Н
V чист зол = Р возд : (g зол) = 20 : (10 20 000) = 110(м) = 100cм
Источник: obrazovalka.com
Полагая что к золоту было подмешано только
1. Как можно на опыте определить, с какой силой тело, погружённое целиком в жидкость, выталкивается из жидкости?
Проведем следующий эксперимент. Подвесим на пружину цепочкой пустое ведерко и груз (а). Далее в емкость с жидкостью опустим груз, при этом всю жидкость, которую груз выдавит из емкости, соберем в стакан (б). Сам же груз поднимется вверх, под действием силы Архимеда.
Жидкость перельем в ведерко, и увидим, что в этом случае груз опустится в емкости, а индикатор вернется на то место, где она был до погружения груза в емкость с жидкость (в). Из этого опыта можно сделать заключение, что весь объем жидкости по его массе будет компенсировать силу выталкивания.
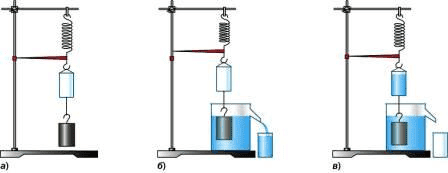
рис. 151. Опыты с ведёрком Архимеда
2. Чему равна эта сила?
Из опыта проведенного выше можно сделать вывод, что сила выталкивающая тело, которое целиком погружённое в жидкость, равна весу жидкости в объёме этого тела. Это и есть архимедова сила.
$F_ = gρ_V_$, где:
$F_$ − архимедова сила,
$ρ_$ − плотность жидкости,
$V_$ − объём погруженного тела.
Как проверить золото йодом / How to test gold with iodine
3. Как называют силу, которая выталкивает тела, погружённые в жидкости и газы?
Выталкивающую силу называют архимедовой силой (или выталкивающей силой), не важно жидкость это или газ.
4. Как подсчитать архимедову силу?
Архимедова сила находится как плотность взятая в объеме тела и она равна:
$F_ = gρ_V_$, где:
$F_$ − архимедова сила,
g − ускорение свободного падения,
$ρ_$ − плотность жидкости,
$V_$ − объём погруженного тела.
5. От каких величин зависит архимедова сила? От каких величин она не зависит?
Из формулы силы Архимеда видно, что она зависит от плотности жидкости, в которую погружаем тело, от объёма этого тела, от условия погружения (полностью или не полностью погружается тело. Однако она не зависит, от плотности вещества самого погружаемого тела, от формы тела.
Упражнение 26
1. К коромыслу весов подвешены два цилиндра одинаковой массы: свинцовый и алюминиевый. Весы находятся в равновесии. Нарушится ли равновесие весов, если оба цилиндра одновременно погрузить в воду; в спирт? Ответ обоснуйте. Проверьте его на опыте.
Как зависит выталкивающая сила от объёма тела?
Из справочной информации мы знаем, что плотность свинца больше плотности алюминия. То есть два подвешенных груза будут иметь разный объем тел. (V=$frac$). В итоге, когда мы погрузим одно и второе тело в жидкость, то получим две разные выталкивающие силы. ($F_ = gρ_V_$). А раз силы будут разные, то и равновесие весов нарушится.
2. К коромыслу весов подвешены два алюминиевых цилиндра одинакового объёма. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, другой — в спирт? Ответ обоснуйте. Зависит ли выталкивающая сила от плотности жидкости?
7 класс
Глава 3. Давление твёрдых тел. жидкостей и газов
§ 51. Архимедова силаСилу, с которой тело, находящееся в жидкости, выталкивается ею, можно рассчитать, как это сделано в параграфе «Действие жидкости и газа на погружённое в них тело». А можно определить её значение на опыте, используя для этого прибор, изображённый на рисунке 151.
Рис. 151. Опыты с ведёрком Архимеда
К пружине подвешивают небольшое ведёрко и тело цилиндрической формы. Растяжение пружины отмечает стрелка на штативе (рис. 151, а). Она показывает вес тела в воздухе. Приподняв тело, под него подставляют отливной сосуд, наполненный жидкостью до уровня отливной трубки.
После чего тело погружают целиком в жидкость (рис. 151, б). При этом часть жидкости, объём которой равен объёму тела, выливается из отливного сосуда в стакан. Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует ещё и сила, выталкивающая его из жидкости.
Если в ведёрко вылить жидкость из стакана (т. е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению (рис. 151, в).
Ведёрко Архимеда
На основании этого опыта можно заключить, что сила, выталкивающая целиком погружённое в жидкость тело, равна весу жидкости в объёме этого тела. Такой же вывод мы получили и в параграфе «Поршневой жидкостный насос».
Если бы подобный опыт проделать с телом, погружённым в какой-либо газ, то он повзятого в объёме тела.
Силу, выталкивающую тело из жидкости или газа, называют архимедовой силой в честь древнегреческого учёного Архимеда, который впервые указал на её существование и рассчитал её значение.
Древнегреческий философ Архимед (287 — 212 до н. э.)
Установил правило рычага, открыл закон гидростатикиИтак, опыт подтвердил, что архимедова (или выталкивающая) сила равна весу жидкости в объёме тела, т. е. FA = Рж = gmж. Массу жидкости mж, вытесняемую телом, можно выразить через её плотность (ρж) и объём тела (Vт), погружённого в жидкость (так как Ѵж — объём вытесненной телом жидкости равен Vт — объёму тела, погружённого в жидкость), т. е. mж = ρжVт.
Следовательно, архимедова сила зависит от плотности жидкости, в которую погружено тело, и от объёма этого тела. Ho она не зависит, например, от плотности вещества тела, погружаемого в жидкость, так как эта величина не входит в полученную формулу.
Определим теперь вес тела, погружённого в жидкость (или в газ). Так как две силы, действующие на тело в этом случае, направлены в противоположные стороны (сила тяжести вниз, а архимедова сила вверх), то вес тела в жидкости P1 будет меньше веса тела в вакууме P = gm (m — масса тела) на архимедову силу FA = gmж (mж — масса жидкости (или газа), вытесненной телом), т. е.
Таким образом, если тело погружено в жидкость (или газ), то оно теряет в своём весе столько, сколько весит вытесненная им жидкость (или газ).
Пример. Определите выталкивающую силу, действующую на камень объёмом 1,6 м 3 в морской воде.
Запишем условие задачи и решим её.
Вопросы:
1. Как можно на опыте определить, с какой силой тело, погружённое целиком в жидкость, выталкивается из жидкости?
2. Чему равна эта сила?
3. Как называют силу, которая выталкивает тела, погружённые в жидкости и газы?
4. Как подсчитать архимедову силу?
5. От каких величин зависит архимедова сила? От каких величин она не зависит?
Упражнения:
Упражнение № 26
1. К коромыслу весов подвешены два цилиндра одинаковой массы: свинцовый и алюминиевый. Весы находятся в равновесии. Нарушится ли равновесие весов, если оба цилиндра одновременно погрузить в воду; в спирт? Ответ обоснуйте. Проверьте его на опыте.
Как зависит выталкивающая сила от объёма тела?
2. К коромыслу весов подвешены два алюминиевых цилиндра одинакового объёма. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, другой — в спирт? Ответ обоснуйте. Зависит ли выталкивающая сила от плотности жидкости?
3. Объём куска железа 0,1дм 3 . Какая выталкивающая сила будет на него действовать при полном его погружении в воду; в керосин?
4. Бетонная плита объёмом 2 м 3 погружена в воду. Какую силу необходимо приложить, чтобы удержать её в воде; в воздухе?
5. Предположив, что корона царя Гиерона в воздухе весит 20 Н, а в воде 18,75 Н, вычислите плотность вещества короны.
Полагая, что к золоту было подмешано только серебро, определите, сколько в короне было золота и сколько серебра.
При решении задачи плотность золота считайте равной 20 000 кг/м 3 , плотность серебра — 10 000 кг/м 3 . Каков был бы объём короны из чистого золота?
По мелким камешкам ходить босыми ногами больно. Почему человек не испытывает боли, если ходит по таким же камням в воде?
Это любопытно.
Легенда об Архимеде
Существует легенда о том, как Архимед пришёл к открытию, что выталкивающая сила равна весу жидкости в объёме тела.
Царь Гиерон (250 лет до н. э.) поручил ему проверить честность мастера, изготовившего золотую корону. Хотя корона весила столько, сколько было отпущено на неё золота, царь заподозрил, что она изготовлена из сплава золота с другими, более дешёвыми металлами. Архимеду было поручено узнать, не ломая короны, есть ли в ней примесь.
Много дней мучила Архимеда эта задача. Взвесить корону было легко, но как найти её объём, ведь корона была очень сложной формы. И вот однажды, находясь в бане, он погрузился в наполненную водой ванну, и его внезапно осенила мысль, давшая решение задачи. Ликующий и возбуждённый своим открытием, Архимед воскликнул: «Эврика! Эврика!», что значит: «Нашёл! Нашёл!»
Архимед заказал два слитка — один из золота, другой из серебра, равные весу короны. Каждый слиток он погружал поочерёдно в сосуд, доверху наполненный водой. Архимед заметил, что при погружении слитка из серебра воды вытекает больше (рис. 152). Затем он погрузил в воду корону и обнаружил, что воды вылито больше, чем при погружении золотого слитка, а ведь он был равен весу короны.
По объёму вытесненной жидкости Архимед определил, что корона была изготовлена не из чистого золота, а с примесью серебра. Тем самым мастер был изобличён в обмане, а наука обогатилась замечательным открытием.
Рис. 152. Задача о золотой короне
Задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. В результате появилось замечательное сочинение «О плавающих телах», которое дошло до нас. В этом сочинении Архимедом сформулировано:
Тела, которые тяжелее жидкости, будучи опущены в неё, погружаются всё глубже, пока не достигают дна, и, пребывая в жидкости, теряют в своём весе столько, сколько весит жидкость, взятая в объёме тел.
Источник: xn—-7sbbfb7a7aej.xn--p1ai





