Сколькими способами могут быть распределены Золотая серебряная и бронзовая медали по итогам

Получи верный ответ на вопрос «В спортивных соревнованиях участвуют 8 команд. Сколькими способами могут быть распределены золотая, серебряная и бронзовая медали, если . » по предмету Математика, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!

Новые вопросы по математике

Цена альбома 4 грн, а книжки-6 грн. Мальчик за книжки заплатил 24 грн. Сколько денег заплатил мальчик за такое же количество альбомов?

Вездеход проехал путь от одного поселка до другого со скоростью 42 км/ч. Он проехал 7 часов со скоростью 36 км/ч. А потом еще 6 ч. Найдите скорость на втором участке движение вездехода

Сколько различных нечетных двкзначных чисел можно записпать с помощью цифр 1.3.5.7.8?
Извиняюсь помогите 4 * (14*-3) = 1

Первое число в последовательности 2/3, а каждое следующее на 4/5 больше предыдущего. Найдите число, которое в этой последовательности на шестом месте.

Главная » Математика » В спортивных соревнованиях участвуют 8 команд. Сколькими способами могут быть распределены золотая, серебряная и бронзовая медали, если каждая команда может получит только одну медаль

Стандартное — «На донышке» — Золото

Источник: 4i5.ru

Комбинаторные задачи

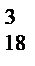
Задача 1.В высшей лиге по футболу 18 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами? (А =18*17*16=4896)

Задача 2 .Сколькими способами можно разложить 28 различных предметов по четырём различным ящикам, так, чтобы в каждом ящике оказалось по 7 предметов?

3. У Влада на обед – первое, второе, третье и пирожное. Он обязательно начнёт с пирожного, а всё остальное съест в произвольном порядке. Найдите число возможных вариантов обеда.

4. Четыре друга купили билеты в кино: на 1-е и 2-е места в первом ряду и на 1-е и 2-е места во втором ряду. Сколькими способами друзья могут занять эти 4 места в кинотеатре? Р4=4!=1×2×3×4=24

5. Ольга помнит, что телефон подруги оканчивается цифрами 5, 7, 8, но забыла, в каком порядке эти цифры следуют. Укажите наибольшее число вариантов, которые ей придётся перебрать, чтобы дозвониться подруге.

6. Семь мальчиков, в число которых входят Сергей и Игорь, становятся в ряд. Найдите число возможных комбинаций, если:

а) Сергей должен находиться в конце ряда;

б) Сергей должен находиться в начале ряда, а Игорь – в конце ряда;

в) Сергей и Игорь должны стоять рядом.

Решение: а) Всего 7 мальчиков на 7 местах, но один элемент фиксирован, не переставляется (Сергей находится в конце ряда). Число возможных комбинаций при этом равно числу перестановок 6 мальчиков, стоящих пред Сергеем: Р6=6!=1×2×3×4×5×6=720. б) Два элемента фиксированы.

Число возможных комбинаций равно числу перестановок 5 мальчиков, стоящих между Сергеем и Игорем: Р5=5!=1×2×3×4×5=120. в) Воспользуемся приёмом «склеивания» элементов. Пусть Сергей и Игорь стоят рядом в порядке СИ. Будем рассматривать эту пару как единый элемент, представляемый с другими пятью элементами.

Стандартное — «Пирокинез» Золотишко

Число возможных комбинаций тогда будет Р6=6!=1×2×3×4×5×6=720. пусть теперь Сергей и Игорь стоят рядом в порядке ИС. Тогда получим ещё Р6=6!=720 других комбинаций. Общее число комбинаций, в которых Сергей и Игорь стоят рядом (в любом порядке) равно 720+720=1440.

Ответ: а) 720; б) 120; в) 1440 комбинаций.

7. Одиннадцать футболистов школьной команды строятся перед началом

матча. Первым становится капитан, вторым – вратарь, а остальные – случайным образом. Сколько существует способов построения?Р9=9!=362880.

8.Сколько существует вариантов опроса 11 учащихся на одном занятии, если ни один из них не будет подвергнут опросу дважды и на занятии может быть опрошено любое количество учащихся, причём порядок, в котором опрашиваются учащиеся, безразличен? Решение: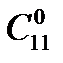

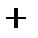
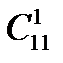
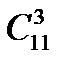
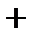
… = 2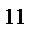

9. Сколькими способами могут быть распределены первая, вторая и третья премии между 13 участниками конкурса?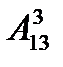

10. Сколькими способами 6 девятиклассников, сдающих экзамен, могут занять места в кабинете, в котором стоит 15 столов?

11. Сколько команд участвовало в финале первенства города по хоккею, если каждая команда сыграла с каждой из остальных по одной игре на своём поле и по одной игре на поле соперника, причём всего было сыграно 30 игр?

Решение: Поскольку каждая пара команд сыграла между собой по две игры (на своём и чужом поле), то выбор пары осуществляется с учётом порядка, т.е. составляются всевозможные размещения из n по 2. По условию задачи =30, отсюда n(n-1) = 6×5, n = 6.Ответ: 6 команд.

12. Имеется три предмета: карандаш, тетрадь и линейка. Сколькими способами из этих канцелярских принадлежностей можно выбрать 2 предмета?

13. В школьной столовой имеются помидоры, огурцы и лук. Сколько различных салатов можно приготовить, если в каждый из них должны входить в равных долях 2 различных вида овощей? (3)

14. Володя идёт на день рождения к одноклассникам, двойняшкам Диме и Ивану. Он хочет подарить каждому из них по мячу. В магазине остались для продажи только 3 мяча разных цветов: белый, чёрный и пятнистый. Сколькими способами, купив 2 мяча, Володя может сделать подарки братьям?(6 способов)

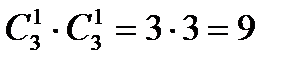
15. В магазине продают кепки трёх цветов: белые, красные и синие. Наташа и Лена покупают себе по одной кепке. Сколько существует различных вариантов покупок для этих девочек?

Источник: helpiks.su

Практические занятия №7,8. Комбинаторика. Правила суммы и произведения. Размещения, перестановки, сочетания.

Правило суммы. Если объект А можно выбрать n способами, а объект В k способами, то объект » А или В » можно выбрать n+k способами.
Правило произведения. Если объект А можно выбрать n способами, а объект В независимо от него k способами, то пару объектов » А и В » можно выбратьn · k способами.

Элементы теории

Размещения без повторений. Размещениями из n элементов по m (m 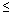n) называются упорядоченные m -элементные выборки из данных n элементов .

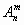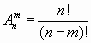
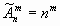
Размещения с повторениями. Размещениями с повторениями из n по m называются упорядоченные m-элементные выборки, в которых элементы могут повторяться.

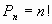
Перестановки без повторений. Перестановками из n элементов называются размещения из n элементов по n.

Пусть (a1,a2,…,an), — перестановка элементов множества .Пара (ai, aj) называется инверсией перестановки, если i < j, то ai > aj.

Таблицей инверсии перестановки (a1,a2,…,an) называется последовательность (d1,d2,…,dn),где dj — число элементов, больших j и расположенных левее j.

Сочетания без повторений. Сочетаниями из n элементов по m (m n) называются неупорядоченные m-элементные выборки из данных n элементов.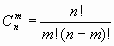

А лгоритм определения вида комбинации

Задания для самостоятельного выполнения

Задание 1.

0) В ящике находятся 20 шаров: 5 белых, 6 черных, 7 синих и 2 красных. Сколькими способами можно взять из ящика один цветной шар?

1) В розыгрыше первенства по футболу принимают участие 18 команд. Сколькими способами могут быть распределены золотая, серебряная и бронзовая медали, если любая команда может получить только одну медаль?

2) При формировании экипажа космического корабля имеется 10 претендентов на пост командира экипажа, 20 — на пост бортинженера и 25 — на пост космонавта-исследователя. Ни один кандидат не претендует одновременно на два поста. Сколькими способами можно выбрать одну из кандидатур или командира, или бортинженера, или космонавта-исследователя?

3) Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной и той же горизон­тали и вертикали?

4) Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну — на правую руку так, чтобы эти перчатки были различных размеров?

5) Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

6) В ящике лежат 4 черных и 3 белых шара. Наудачу вынимаются последовательно два шара. Какова вероятность того, что оба эти шара окажутся белыми? (Шар после выбора в ящик не возвращается.)

7) В столовой предлагают два различных первых блюда a1 и а2, три различных вторых блюда b1, b2, b3 и два вида десерта с1 и c2. Сколько различных обедов из трех блюд может предложить столовая?

8) У англичан принято давать детям несколько имен. Сколь­кими способами можно назвать ребенка, если общее число имен равно 300, а ему дают не более трех имен?

9) На вершину горы ведут пять дорог. Сколькими способами турист может подняться на гору и спуститься с нее? То же самое при условии, что спуск и подъем происходят по разным путям.

Задание 2.

0) Составьте все слова из трех букв А, В, С по две буквы.

1) В классе 30 учащихся. Сколькими способами можно выбрать из класса команду из 4 учащихся для участия в олимпиаде по истории?

2) Сколькими способами можно составить двуцветный полоса­тый флаг, если имеется материал 5 различных цветов? Та же за­дача, если одна из полос должна быть красной?

3) Из состава конференции, на которой присутствует 45 чело­века, надо избрать делегацию из 6 человек. Сколькими способами это можно сделать?

4) В турнире принимают участие 8 команд. Сколько различных предположений относительно распределения трех первых мест можно сделать?

5) Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различны и нечетны?

Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, если имеется материя 6 различных цветов?

Сколько существует трехзначных чисел, в записи которых цифры 1, 2, 3 встречаются ровно по одному разу?

На полке стоят 5 книг. Сколькими способами можно выложить в стопку несколько из них (стопка может состоять и из одной книги)?

У Димы есть 5 шариков: красный, зеленый, желтый, синий и золотой. Сколькими способами он сможет украсить ими 5 елок, если на каждую требуется надеть ровно один шарик?

Задание 3.

0) Сколько четырехбуквенных «слов» можно составить из букв «М» и «А»?

1) Сколькими способами можно разместить восемь пассажиров в три вагона?

2) Каждый телефонный номер состоит из семи цифр. Сколько всего телефонных номеров, не содержащих других цифр, кроме 2, 3, 5 и 7?

3) Четверо студентов сдают экзамен. Сколькими способами мо­гут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки?

4) Сколько различных трехбуквенных слов можно составить из 32 букв алфавита (со смыслом и без)?

5) В селении проживает 2000 жителей. Доказать, что, по край­ней мере, двое из них имеют одинаковые инициалы.

Сколькими способами можно покрасить пять елок в серебристый, зеленый и синий цвета, если количество краски неограниченно, а каждую елку можно покрасить только в один цвет?

Каждую клетку квадратной таблицы 2 × 2 можно покрасить в черный или белый цвет. Сколько существует различных раскрасок этой таблицы?

Сколькими способами можно заполнить одну карточку в лотерее «Спортпрогноз»’? Указание: в этой лотерее нужно предсказать итог тринадцати спортивных матчей. Итог каждого матча — победа одной из команд либо ничья; счет роли не играет.

Алфавит племени Мумбо-Юмбо состоит из трех букв А, Б и В. Словом является любая последовательность, состоящая не более, чем из 4 букв. Сколько слов в языке племени Мумбо-Юмбо? Указание: сосчитайте отдельно количества одно-, двух-, трех- и четырехбуквенных слов.

Задание 4.

0) Сколькими способами можно расставить 7 книг на книжной полке?

1) Сколькими способами можно разложить 8 различных писем по 8 различным конвертам, если в каждый конверт кладется только одно письмо?

2) Сколько ожерелий можно составить из семи бусин раз­ных размеров?

3) Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом?

4) Сколько слов можно получить, переставляя буквы в слове «градус»?

5) Сколькими различными способами можно рассадить 6 человек на 6 креслах в кинотеатре?

6) Сколько всего шестизначных четных чисел можно составить из цифр 1, 3, 4, 5, 7 и 9, если из этих чисел ни одна не повторяется?

7) Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли взять друг друга?

8) Сколько всего семизначных четных чисел можно составить из цифр 0, 2, 3, 5, 7 и 9, если из этих чисел ни одна не повторяется?

9) Как велико число различных отображений, переводящих множество из n элементов в себя?

Задание 5.

0) Составьте все сочетания из трех букв А, В, С по две буквы.

1) У 6 взрослых и 11 детей обнаружены признаки инфекционного заболевания. Чтобы проверить заболевание, следует взять выборочный анализ у 2 взрослых и 3 детей. Сколькими способами можно это сделать?

2) Сколькими способами можно группу из 20 студентов разделить на две подгруппы так, чтобы в одной группе было 13, а в другой 7 человек?

3) На книжной полке стоят 3 книги по алгебре, 4 книги по геометрии и 5 книг по литературе. Сколькими способами можно взять с полки три книги по математике?

4) Учащийся хочет использовать для раскраски географической контурной карты 4 краски из 6, которые он имеет в своем распоряжении. Сколькими способами он может выбрать 4 краски из 6?

5) Даны две параллельные прямые. На одной из них имеется 10 точек, а на другой — 20. Сколько существует треугольников с вершинами в данных точках?

6) Сколькими способами можно распределить 28 костей домино между 4 игроками так, чтобы каждый получил 7 костей?

7) В классе 12 юношей и 13 девушек. Сколькими способами из них можно выбрать четырех учащихся для дежурства на вечере, если а) освободить девушек; б) юноши и девушки?

8) Сколькими способами абитуриент может выбрать 3 ВУЗа из 5 для подачи документов?

Задание 6.

0) Из города А в город В ведут пять дорог, а из города В в город С – три дороги. Сколько путей, проходящих через В, ведут из А в С?

1) Из двух спортивных обществ, насчитывающих по 100 фехто­вальщиков каждое, надо выделить по одному фехтовальщику для участия в состязании. Сколькими способами может быть сделан этот выбор?

2) Имеется пять видов конвертов без марок и четыре вида ма­рок одного достоинства. Сколькими способами можно выбрать кон­верт с маркой для посылки письма?

3) Сколькими способами можно выбрать гласную и согласную буквы из слова «камзол»?

4) Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?

5) Бросают игральную кость с шестью гранями и запускают волчок, имеющий восемь граней. Сколькими различными способами они могут упасть?

6) На вершину горы ведут пять дорог. Сколькими способами •турист может подняться на гору и спуститься с нее? То же самое при условии, что спуск и подъем происходят по разным путям.

7) На ферме есть 20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?

8) Сколькими способами можно указать на шахматной доске два квадрата – белый и черный? А если нет ограничений на цвет выбранных квадратов?

9) Из 12 слов мужского рода, 9 женского и 10 среднего надо выбрать по одному слову каждого рода. Сколькими способами мо­жет быть сделан этот выбор?

Задание 7.

0) В местком избрано 9 человек. Из них надо выбрать предсе­дателя, заместителя председателя, секретаря и культорга. Сколь­кими способами это можно сделать?

1) Из состава конференции, на которой присутствует 52 чело­века, надо избрать делегацию, состоящую из 5 человек. Сколькими способами это можно сделать?

2) Автомобильные номера состоят из одной, двух или трех букв и четырех цифр. Найти число таких номеров, если используют­ся 32 буквы русского алфавита.

3) Сколько различных перестановок можно получить, переставляя бук­вы в слове «математика»? В слове «парабола»?

4) В почтовом отделении продаются открытки 10 сортов. Сколь­кими способами можно купить в нем 12 открыток? Сколькими спо­собами можно купить 8 открыток?

5) Из группы, состоящей из 7 мужчин и 4 женщин, надо вы­брать 6 человек так, чтобы среди них’ было не менее 2 женщин. Сколькими способами это можно сделать?

6) Четверо студентов сдают экзамен. Сколькими способами мо­гут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки?

7) Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется хотя бы один туз?

8) Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется ровно один туз?

9) Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется ровно два туза?

Источник: infopedia.su