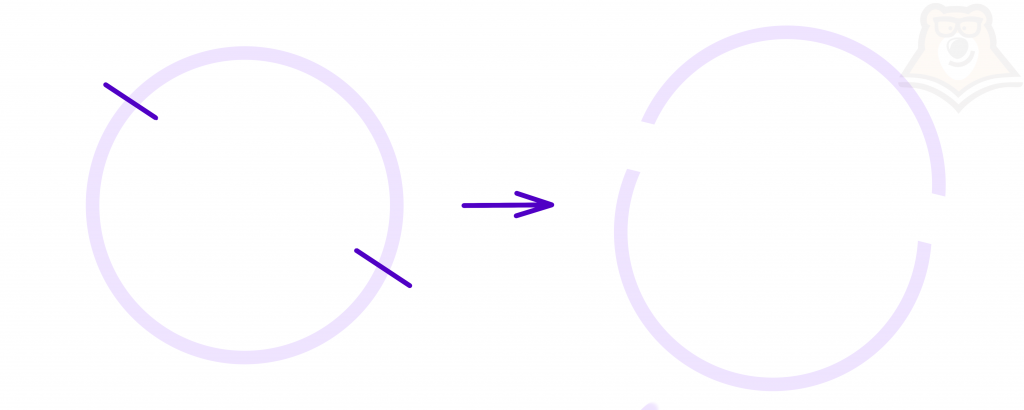
Под стороной двумерной фигуры мы понимаем классы эквивалентности точек ранга 1. Здесь есть три эквивалентных класса. у квадрата четыре стороны и четыре угла, а у круга только одна сторона и нет углов.
Сколько сторон у круга ответ?
Круг — это бесконечно длинная линия. Там только две стороны любой линии. Следовательно, у Круга только ДВЕ стороны.
Есть ли стороны в круге?
Если вы думаете о круге как о диске, то у него есть верхняя и нижняя стороны. Если вы думаете об этом как о кривой, то у нее есть внутренняя и внешняя стороны. Если вы думаете об этом как о границе n-стороннего правильного многоугольника, то можно оправдать ответ, что у круга бесконечно много бесконечно малых сторон.
Сколько сторон у круга в Википедии?
Если вы думаете о круге как о диске, то у него есть верхняя и нижняя стороны. Если вы думаете об этом как о кривой, то у нее есть внутренняя и внешняя стороны. Если вы думаете об этом как о пределе n-стороннего правильного многоугольника, то можно оправдать ответ, что круг имеет бесконечно много бесконечно малых сторон.
Сколько Сторон У Круга? [Vsauce 2 на русском]
Сколько ребер было у круга?
В круге было бы нулевые края под этим определением. Для многоугольников эти два определения совпадают. В любом случае у квадрата четыре ребра, а у n-угольника — n. Вы, вероятно, также могли бы создать подходящее определение, которое было таким же для многоугольников, но для круга дает вам только одно ребро.
У круга 0 или 1 сторона?
квадрат имеет четыре стороны и четыре угла, а у круга только одна сторона и нет углов. что треугольник Рело имеет три стороны и три угла.
Как называется фигура с одной стороной?
1 сторона. моногон (невозможная фигура в евклидовой геометрии) 2 стороны. Digon.
Круг прямой?
Поскольку у круга бесконечные стороны, внутренние углы круга равны 180 градусов, что является прямая линия.
Возможны ли идеальные круги?
Это не значит, что идеального круга или сферы где-то не существует. . Чтобы круг был идеальным, мы бы нужно измерить бесконечное количество точек по окружности круга знать наверняка.
Какая форма имеет больше всего сторон?
В геометрии мириагон или 10000-угольник представляет собой многоугольник с 10 000 сторонами.
.
Мириагон.
| Тип | Правильный многоугольник |
| Ребра и вершины | 10000 |
| Символ Шлефли | , t , tt , ttt , tttt |
| Диаграмма Кокстера |
Бесконечны ли многоугольники?
В геометрии апейрогон (от греческих слов «ἄπειρος» apeiros: «бесконечный, безграничный» и «γωνία» gonia: «угол») или бесконечный многоугольник — это обобщенный многоугольник со счетно бесконечным числом сторон.
.
Апейрогон.
| Диаграмма Кокстера | |
| Внутренний угол (градусы) | 180° |
| Двойной многоугольник | Самодвойственный |
Источник: ch-pik.ru
Сколько сторон у круга?
Круг — часть плоскости, ограниченная окружностью. Нет математического определения, что называть стороной круга. Интуитивно представляется правильным ответ: у круга две стороны: внутренняя и внешняя. Внутренняя сторона — это все точки плоскости, лежащие внутри круга, внешняя — это все точки плоскости, лежащие вне круга.
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное ссылка отблагодарить
mycha tik [30.3K]
8 месяцев назад
Для начала определимся — что такое сторона:
Как мы знаем, круг — это геометрическая фигура, ограниченная окружностью.
Так как, по определению, окружность — замкнутая кривая, а не отрезок прямой и ограничивает круг полностью, то и стороной она быть не может. Или может?
Попробуем порассуждать. Чтобы получить сторону, мы должны взять две различные конечные точки и соединить их прямой линией. Для окружности так не получится. Любая прямая может иметь только одну точку касания к окружности. Вторая точка будет уже за её пределами. А если длина прямой будет равна точке?
И количество этих точек будет равно количеству всех точек окружности? В этом случае мы уже имеем дело с апейрогоном.
Это свойство окружности позволяет строить имеющие стороны «круги» из мелких квадратов-пикселей, но для человеческого глаза они выглядят круглыми.

А в программе 3D дизайна SketchUp, даже 24-угольник уже воспринимается как круг, а не как многоугольник:

Поэтому, ответ на заданный вопрос может звучать так: у круга ноль или бесконечное количество сторон.
Источник: www.bolshoyvopros.ru
Окружность и круг
Оглянитесь вокруг: геометрические фигуры окружают нас повсюду, а в математике и вовсе встречаются почти в каждом задании. Не стали исключением и окружность и круг, которые попадают в задачки чаще, чем может показаться. Поэтому эта статья будет полезна: овладеете всеми премудростями, необходимыми для жизни и экзаменов.
Обруч и окружность
Давайте вспомним один из предметов инвентаря художественной гимнастики – обруч. Это узкое кольцо большого диаметра, внутри которого ничего нет. Обруч состоит только из “контура”, то есть из того самого кольца. Именно с помощью обруча мы приближаемся к термину “окружность”.

Окружность – это замкнутая кривая, все точки которой равноудалены от центра.
Разберем чуть подробнее, что значит фраза “равноудалены от центра”. Допустим, мы точно знаем, где центр нашего обруча, и через этот центр натянем много-много ленточек. Тогда окажется, что длина каждой ленточки от центра до обруча будет одинаковой.
То есть окружность состоит из бесконечного множества точек, которые располагаются на равном расстоянии от центра.
Элементы окружности
Радиус – это отрезок, построенный от центра окружности до любой точки на окружности.
Если вспомнить обруч с ленточками, то одна ленточка – это радиус. Радиус обозначается буквой R. В окружности можно построить множество радиусов, и все они будут равны между собой.
Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
Можно сразу заметить, что диаметр будет состоять из двух радиусов, которые проведены по разные стороны от центра окружности.
Диаметр обозначается буквой D и равняется двум радиусам.
Хорда – это отрезок, соединяющий две любые точки на окружности. При этом хорда не обязательно проходит через центр окружности.
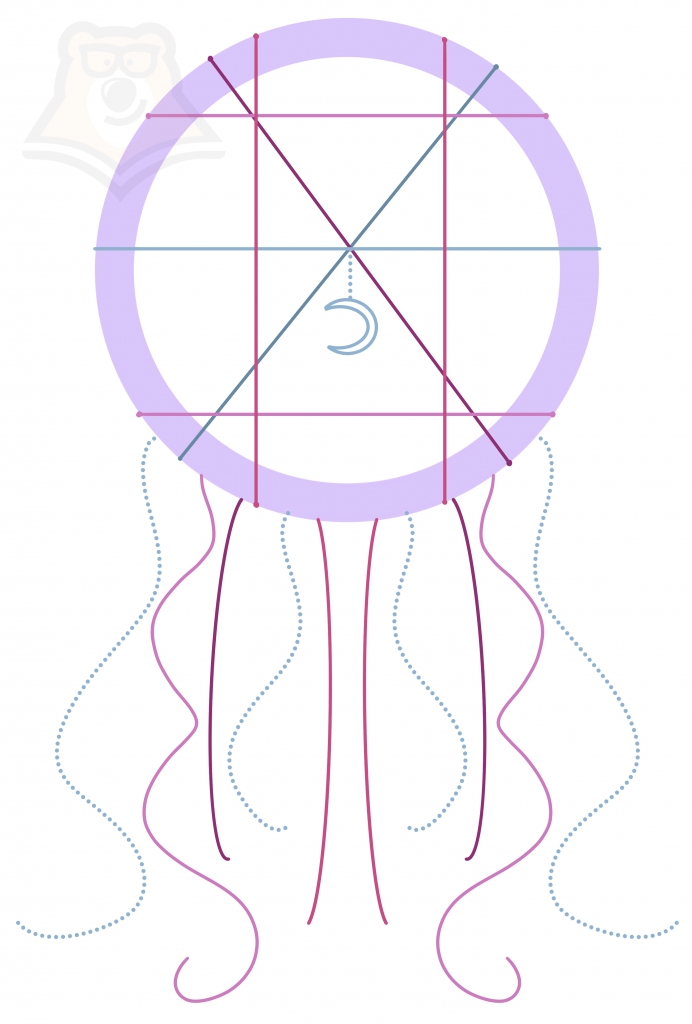
Таким образом, хорда может иметь любой размер и любое направление, главное, чтобы ее начало и конец лежали на окружности.
Рассмотрим свойства хорды.
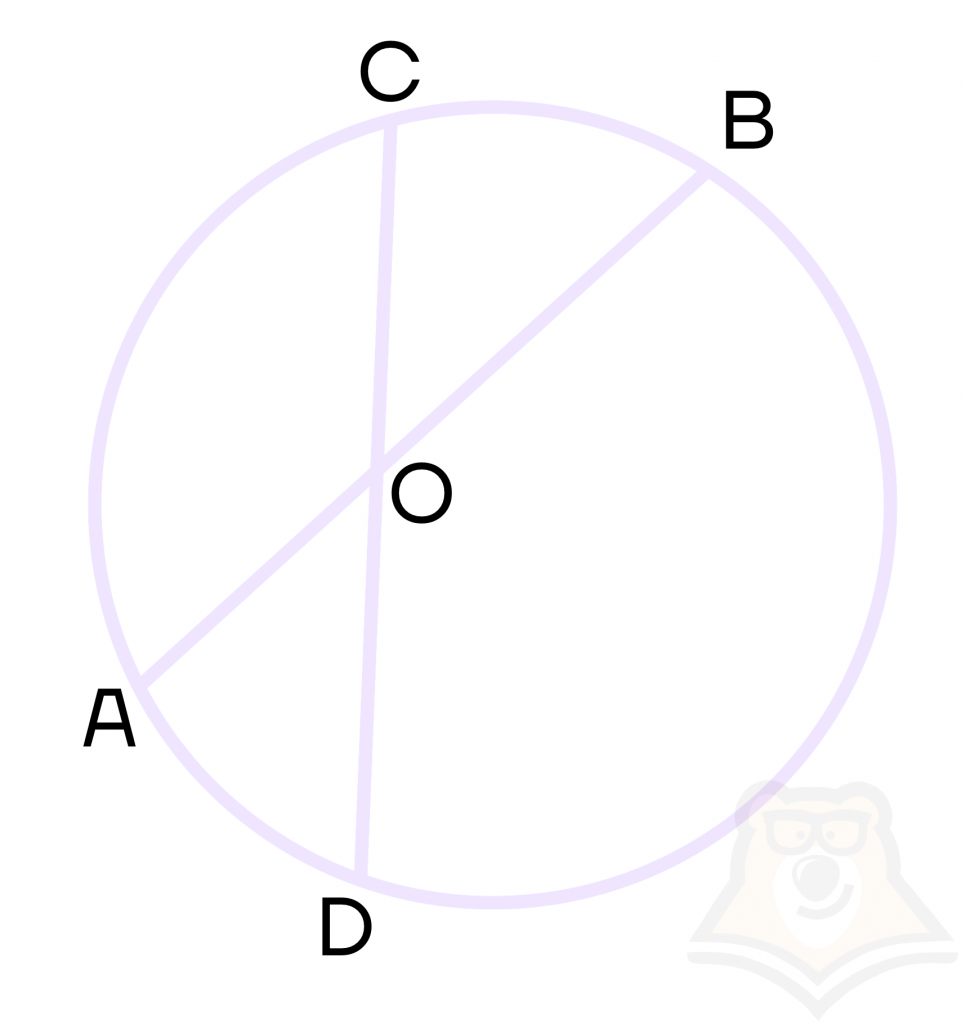
1 свойство. При пересечении двух хорд произведения их отрезков равны.
Пусть в окружности проведены хорды АВ и CD, которые пересекаются в точке О. Тогда выполняется равенство АО * ОВ = СО * OD.
2 свойство. Равные хорды стягивают равные дуги.
3 свойство. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ей дуги пополам.
Если диаметр CD перпендикулярен хорде АВ, то АЕ = ЕВ.
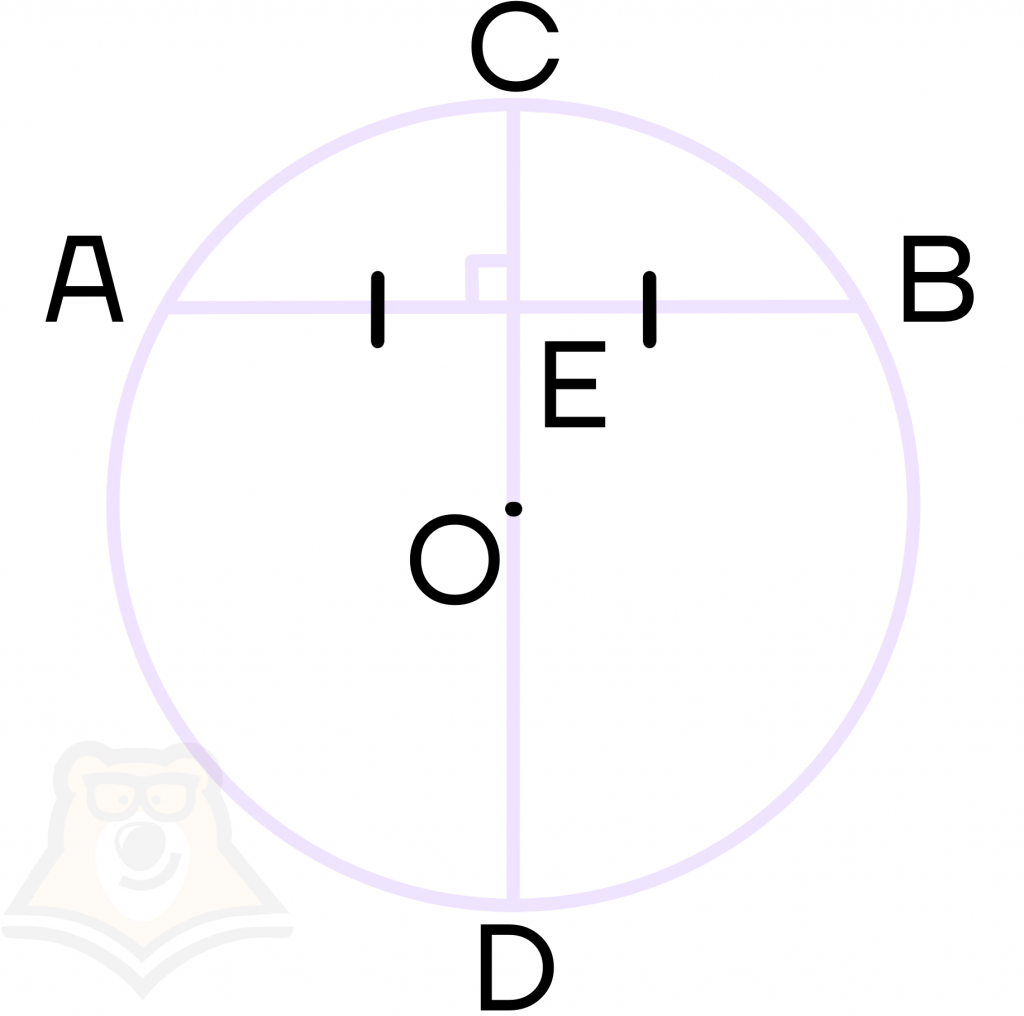
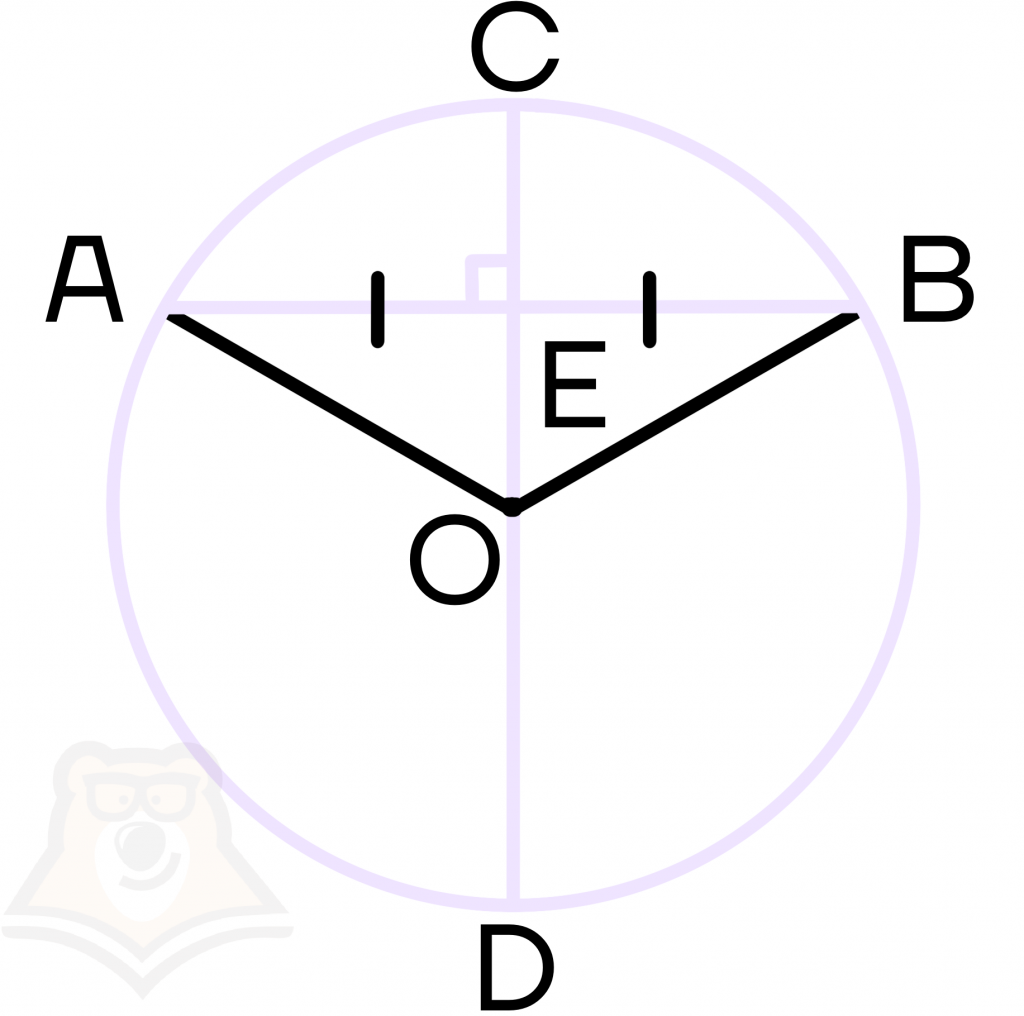
Рассмотрим, почему выполняется это свойство. Достроим треугольник АОВ, в котором АО и ОВ – радиусы. Радиусы в окружности равны, следовательно, треугольник равнобедренный.
Рассмотрим ОЕ – высота в равнобедренном треугольнике, проведенная к основанию.
Высота в равнобедренном треугольнике, проведенная к основанию, совпадает с медианой и биссектрисой, следовательно, ОЕ – медиана, а значит АЕ = ЕВ.
Свойство 4. Угол между пересекающимися хордами окружности равен половине суммы дуг, заключенных между ними.
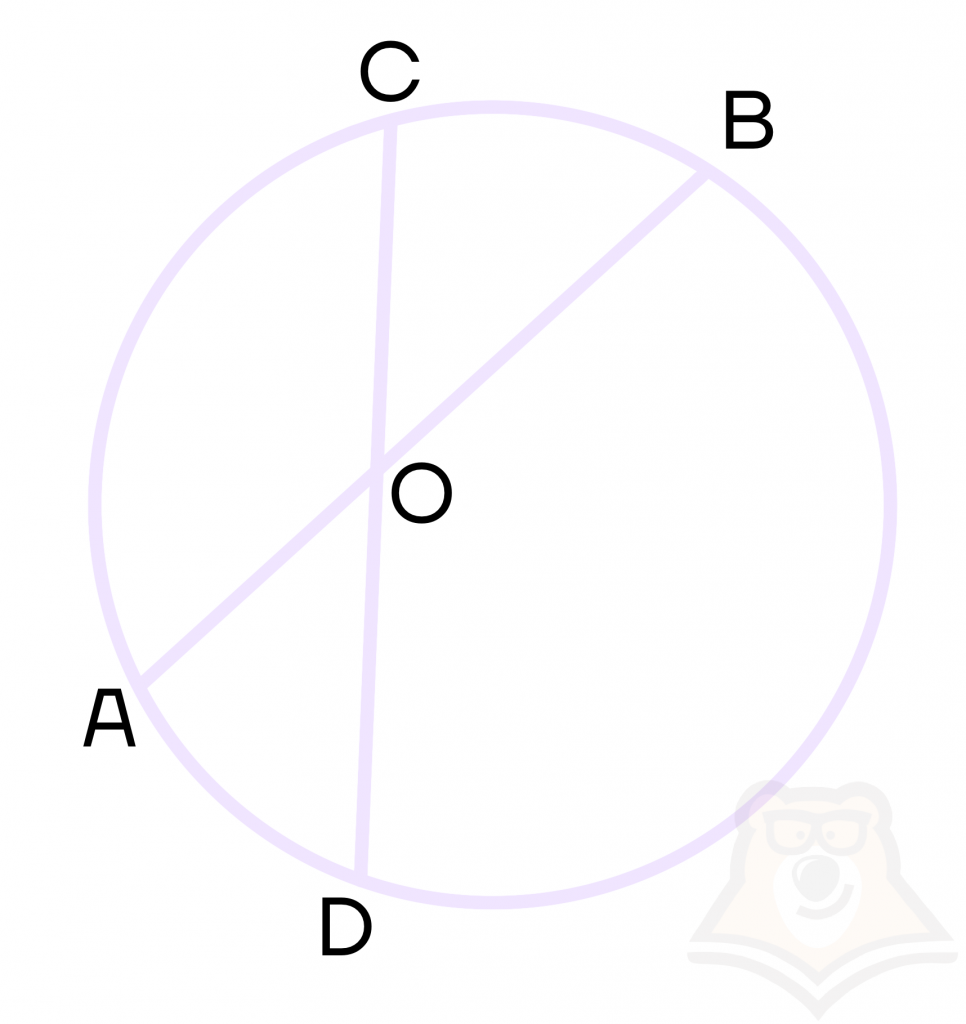
Заметим, что углы COB и AOD равны между собой, поскольку являются вертикальными.
Дуга – это часть окружности, началом и концом которой являются две произвольные точки.
Допустим, из нашего обруча вырежут какую-то часть. Тогда и вырезанная часть, и оставшаяся часть будут дугами.