Электронный газ металла, находящийся в основном состоянии при абсолютном нуле, заполняет в — пространстве все состояния внутри некоторой сферы, которая называется поверхностью Ферми. Энергия, соответствующая этой поверхности, называется энергией Ферми и представляет максимальную энергию, что могут иметь электроны при абсолютном нуле температур. Таким образом, поверхность Ферми отделяет в — пространстве занятые состояния от свободных.
Определим величину энергии Ферми через концентрацию электронов Для этого проинтегрируем (4.76) по всем возможными значениями энергии и учтем, что при функция равняется единице для всех и нулю для всех
Отсюда энергия Ферми при равна
Для отличной от абсолютного нуля температуры энергия Ферми будет являться функцией температуры
Поскольку в металлах при любой температуре , то положение уровня Ферми в металлах определяется лишь концентрацией свободных электронов и практически не изменяется с температурой.
Скорость электронов на поверхности Ферми и температура Ферми определяются через энергию Ферми
Загадки физики элементарных частиц / Дмитрий Казаков в Рубке ПостНауки
Оценим величину энергии Ферми для типичного металла, считая концентрацию электронов :
Среднюю энергию электронов можно определить через энергию Ферми
Следовательно, средняя энергия электронов по порядку величины совпадает с энергией Ферми. Такой энергией молекулы классического газа обладали бы при температуре в несколько десятков тысяч градусов. Это свидетельствует о том, что электронный газ в металлах находится в особом, вырожденном состоянии. Его энергия практически не зависит от температуры.
В том случае, когда фермиевская функция распределения переходит в максвелловскую, вырождение с электронного газа снимается. Это возможно при выполнении условия
Выразим это условие через параметры электронного газа. Для этого проинтегрируем (4.76) с учетом (4.83):
Отсюда условие снятия вырождения с электронного газа может быть представлено в виде
Обратное неравенство означает, что электронный газ находится в вырожденном состоянии.
Если приравнять левую часть неравенства (4.84) единице, можно определить температуру снятия вырождения:
Оценивая величину этой температуры для концентрации электронов м -3 , получим К.
Таким образом, электронный газ в металлах всегда находится в вырожденном состоянии.
В заключение заметим, что поверхность Ферми является сферической только в приближении свободных электронов. Для реальных металлов, когда закон дисперсии носит сложный характер, вид поверхности Ферми может быть весьма экзотическим (рис. 4.18).
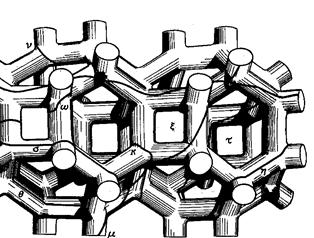 |
| Рис.4.18. Поверхность Ферми для реальных металлов |
Источник: studopedia.ru
Задачи на распределение Ферми-Дирака
Задача №1
Энергетические уровни. 8 класс.
До какой температуры нужно нагреть классический электронный газ, чтобы средняя энергия его электронов была равна средней энергии свободных электронов в серебре при Т = 0 К? Энергия Ферми серебра EF.
Решение

Задача №2
Воспользовавшись распределением свободных электронов в металле по энергиям, найдите отношение средней скорости свободных электронов к их максимальной скорости при Т = 0.
Решение

Задача №3
Воспользовавшись распределением свободных электронов в металле по энергиям, найдите отношение средней кинетической энергии свободных электронов в металле при температуре Т = 0 к их максимальной энергии.
Решение

Задача №4
Определите отношение концентраций электронов проводимости при Т = 0 в литии и цезии, если известно, что уровни Ферми в этих металлах при Т = 0 имеют значения, равные E1F и E2F.
Решение

Задача №5
Воспользовавшись распределением свободных электронов в металле по энергиям при температуре Т = 0, получите распределение электронов по импульсам.
Решение

Источник: enlib.ru