У николая были только серебряные монеты зато появилось 55

Заметим, что на конечный результат не влияет порядок, в котором Николай будет выполнять операции. Пусть он совершит х операций первого типа и y операций второго типа. Условие задачи тогда можно записать так:
x+y=50 (1)
3y-2x=0
серебряных монет станет на 5y-3x меньше.
решим систему (1) y=30 x=20. Тогда серебряных монет станет на 150-60=90

Источник: reshaika.com

Презентация по математике Мячиной В. (10 «Б» класс) на тему » Задачки из ЕГЭ №20″

Задание: Экзамен включает 30 заданий. За каждое верно выполненное задание ученик получает 3 балла, за неверный ответ снимают 2 балла, задание без ответа не приносит баллы и не отнимает их. Какое максимальное количество ошибок мог допустить ученик, если в итоге он получил 44 балла? Решение: Пусть x заданий решено верно, y — с ошибкой и n — не решено вообще.

ВСЕ ЗАДАНИЯ 20 | ЕГЭ БАЗА 2018 | ШКОЛА ПИФАГОРА

Тогда всего задач x+y+n=30, и получено баллов 3x+2y=44. Подставив x=30-n-y во второе уравнение получим: 5y=46-3n. Выбираем значение n таким, чтобы количество ошибок было максимально и y осталось целым числом, т.е. n=2. 5y=46-3⋅2=40. y=8 — максимальное количество ошибок с результатом 44 балла Ответ: 8

№ слайда 3

Задание: Улитка за день залезает вверх по дереву на 2 м, а за ночь сползает на 1 м. Высота дерева 9 м. За сколько дней улитка доползет до вершины дерева? Ответ: 8 Решение: Заметим, что в этой задаче следует различать понятие «сутки» и понятие «день». В задаче спрашивается именно за сколько дней улитка доползет до вершины дерева.

За один день улитка поднимается на 2 м, а за одни сутки улитка поднимается на 1 м (за день поднимается на 2 м, а потом за ночь спускается на 1 м). За 7 суток улитка поднимается на 7 метров. То есть утром 8-го дня ей останется доползти до вершины 2 м. И за восьмой день она преодолеет это расстояние.

№ слайда 4

Задание: В корзине лежат 30 грибов: рыжики и грузди. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов хотя бы один груздь. Сколько рыжиков в корзине? Решение: Так как среди любых 12 грибов имеется хотя бы один рыжик (или больше) число груздей должно быть меньше или равно чем 12-1=11 Отсюда следует, что число рыжиков больше или равно чем 30-11=19 Так как среди любых 20 грибов хотя бы один груздь (или больше), число рыжиков должно быть меньше или равно чем 20-1=19 Тогда получили, что с одной стороны, число рыжиков больше или равно чем 19, а с другой — меньше или равно чем 19. Следовательно, число рыжиков равно 19. Ответ: 19

Серебряная монета. 1Рубль 1897г. Император Николай 2 #монета #серебро #коп #мд #металлоискатель

№ слайда 5

3адание: Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На каком этаже живёт Саша? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.) Ответ: 2

№ слайда 6

Задание: Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 9 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 56 очков, если известно, что по крайней мере один раз он ошибся? Ответ: 17

№ слайда 7

Задание: Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 352, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало? Ответ: 85

№ слайда 8

Задание: Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 8 проводов. сколько всего проводов протянуто между этими десятью столбами? Ответ: 40

№ слайда 9

Задание: В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения . Произведение получившихся чисел оказалось равным 3495 . Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки 2, 3, 4 или 5 и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; 2,8 — до 3) Ответ: 3

№ слайда 10

Задание: Среднее арифметическое 6 различных натуральных чисел равно 8. На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 1 больше? Ответ: 6

№ слайда 11

Задание: Прямоугольник разбит на четыре маленьких прямоугольника двумя прямолинейными разрезами. Площади трех из них, начиная с левого верхнего и далее по часовой стрелке равны 15, 18, 24. Найдите площадь четвертого прямоугольника. Ответ: 20

№ слайда 12

№ слайда 13

Задание: На поверхности глобуса фломастером проведены 17 параллелей и 24 меридиана. На сколько частей проведённые линии разделяют поверхность глобуса? Меридиан – это дуга окружности, соединяющая Северный и Южный полюса. параллель – это окружность, лежащая в плоскости, параллельной плоскости экватора. Ответ: 432

№ слайда 14

№ слайда 15

Задание: Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр – на 1600 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров? Ответ: 89100

№ слайда 16

Задание: Маша и Медведь съели 100 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну? Ответ: 90

№ слайда 17

Задание: На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 5 кусков, если по жёлтым – 7 кусков, а если по зелёным – 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов? Ответ: 21

№ слайда 18

Задание : На прилавке цветочного магазина стоят 3 вазы с розами: оранжевая, белая и синяя. Слева от оранжевой вазы 15 роз, справа от синей вазы 12 роз. Всего в вазах 22 розы. сколько роз в оранжевой вазе? Ответ: 7

№ слайда 19

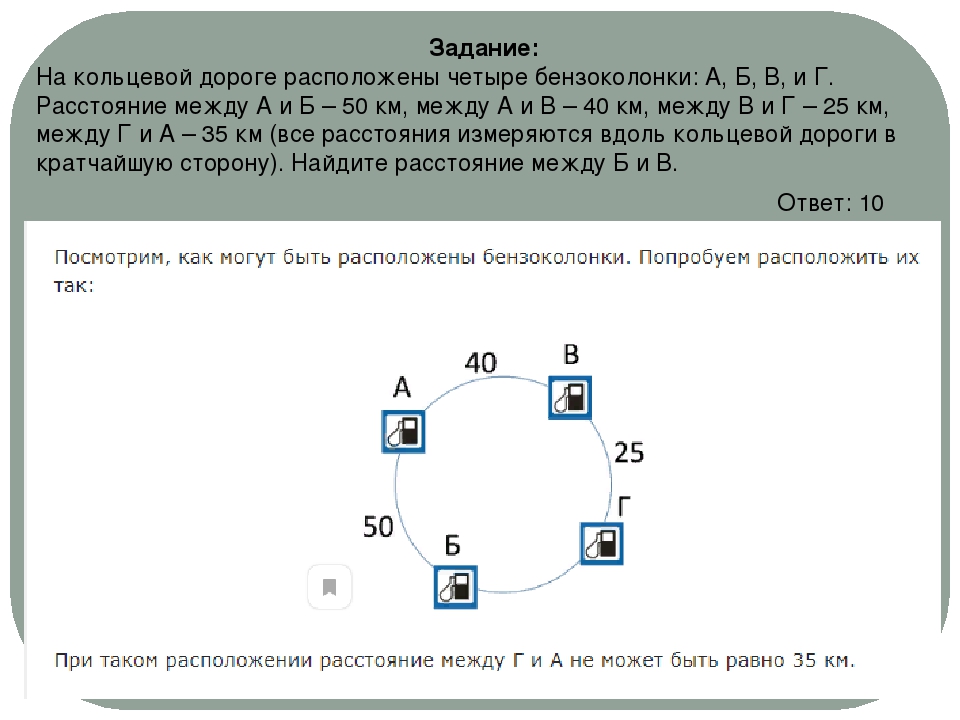
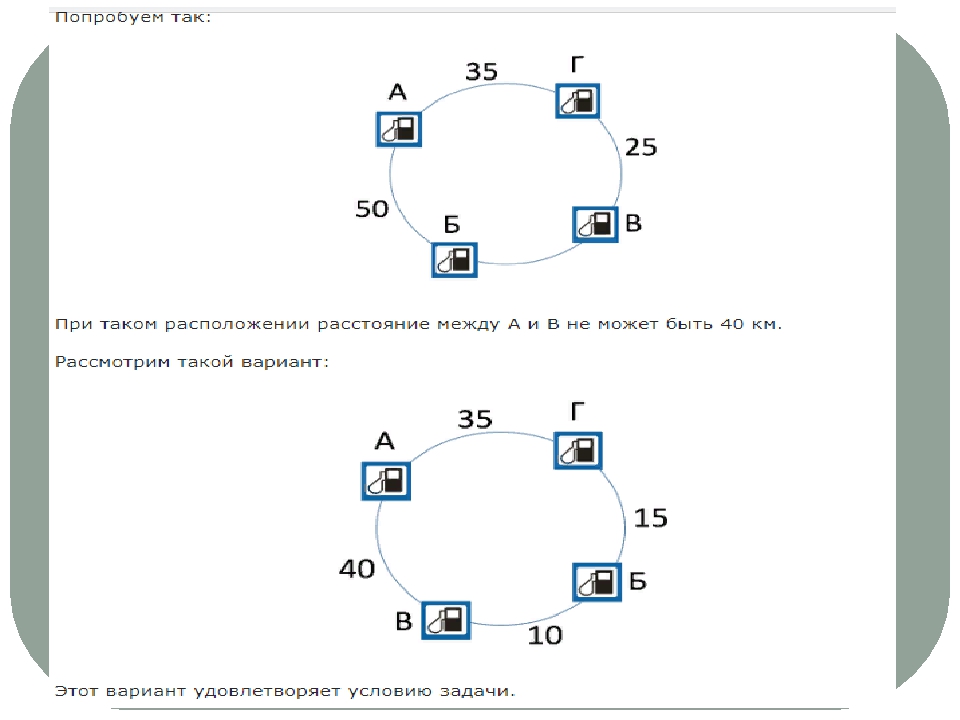
Задание: На кольцевой дороге расположены четыре бензоколонки: A, Б, B, и Г. Расстояние между A и Б – 50 км, между A и В – 40 км, между В и Г – 25 км, между Г и A – 35 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между Б и В. Ответ: 10

№ слайда 20

№ слайда 21

Задание: Во всех подъездах дома одинаковое число этажей, а на каждом этаже одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 105 квартир? Ответ: 7

№ слайда 22

Задание: В таблице три столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 72, во втором – 81, в третьем – 91, а сумма чисел в каждой строке больше 13, но меньше 16. Сколько всего строк в таблице? Ответ:17

№ слайда 23

Задание: Три луча, выходящие из одной точки, разбивают плоскость на три разных угла, измеряемых целым числом градусов. Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла? Ответ: 20

№ слайда 24

В обменном пункте можно совершить одну из двух операций: за 2 золотые монеты получить 3 серебряные и одну медную за 5 серебряных монет получить 3 золотые и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 5050 медных. На сколько уменьшилось количество серебряных монет у Николая? Ответ: 10

№ слайда 25

Сколькими способами можно выложить в ряд три одинаковых красных шарика, два одинаковых зелёных шарика и один синий шарик? Ответ: 60

№ слайда 26

№ слайда 27

Альпинист поднимается на гору высотой 300300 метров. Первые 5050 метров он преодолевает за 1010 минут, каждые следующие 5050 метров — на 22 минуты дольше, чем предыдущие. После отдыха на вершине в течение 3030 минут альпинист начинает спуск с равномерной скоростью 55 минут на каждые 5050 метров. Через сколько часов альпинист снова окажется у подножия горы?

№ слайда 28

В лотке 30 яиц: белые и рябые. Известно, что среди любых 12яиц имеется хотя бы одно рябое, а среди любых 20 яиц хотя бы одно белое. Сколько белых яиц в лотке? Ответ: 11 Так как среди любых 12 яиц имеется хотя бы одно рябое, то белых яиц не может быть больше 11. А поскольку среди любых 20 яиц хотя бы одно белое, то рябых яиц не может быть больше 19.

Так как всего в лотке 30 яиц, то единственный возможный вариант — в лотке 19 рябых яиц и 11 белых.

Источник: urokimatematiki.ru

У николая были только серебряные монеты зато появилось 55

• Вы здесь:
• Главная
• Викторины и олимпиады
• Математика
• Олимпиада по математике

Сайты партнеры:

Не торопитесь уходить!

Помните, что лучшим стимулом для развития сайта, является ваша активность на нем.

Проведите на ресурсе больше времени, попробуйте найти для себя еще что-то интересное в разных каталогах, дайте ссылку на сайт знакомым, напишите на форуме в разделе замечания и предложения что бы вы хотели увидеть нового и необходимые Вам материалы будут добавлены быстрее.

Для быстрого поиска по странице используйте комбинацию клавиш Ctrl+F и в появившемся окне напечатайте слово запроса (или первые буквы)

Олимпиада по математике

Каж­дую се­кун­ду бак­те­рия де­лит­ся на две новые бак­те­рии. Из­вест­но, что весь объём од­но­го ста­ка­на бак­те­рии за­пол­ня­ют за 1 час. За сколь­ко се­кунд бак­те­рии за­пол­ня­ют по­ло­ви­ну ста­ка­на?
Ответ: 3599

На палке от­ме­че­ны по­пе­реч­ные линии крас­но­го, жёлтого и зелёного цвета. Если рас­пи­лить палку по крас­ным ли­ни­ям, по­лу­чит­ся 15 кус­ков, если по жёлтым — 5 кус­ков, а если по зелёным — 7 кус­ков. Сколь­ко кус­ков по­лу­чит­ся, если рас­пи­лить палку по ли­ни­ям всех трёх цве­тов?
Ответ: 25

Куз­не­чик пры­га­ет вдоль ко­ор­ди­нат­ной пря­мой в любом на­прав­ле­нии на еди­нич­ный от­ре­зок за один пры­жок. Куз­не­чик на­чи­на­ет пры­гать из на­ча­ла ко­ор­ди­нат. Сколь­ко су­ще­ству­ет раз­лич­ных точек на ко­ор­ди­нат­ной пря­мой, в ко­то­рых куз­не­чик может ока­зать­ся, сде­лав ровно 11 прыж­ков?
Ответ: 12

Саша при­гла­сил Петю в гости, ска­зав, что живёт в седь­мом подъ­ез­де в квар­ти­ре № 462, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом се­ми­этаж­ный. На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)
Ответ: 5

Саша при­гла­сил Петю в гости, ска­зав, что живёт в вось­мом подъ­ез­де в квар­ти­ре № 468, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом две­на­дца­ти­этаж­ный. На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)
Ответ: 10

Саша при­гла­сил Петю в гости, ска­зав, что живёт в две­на­дца­том подъ­ез­де в квар­ти­ре № 465, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом пя­ти­этаж­ный. На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)
Ответ: 4

Саша при­гла­сил Петю в гости, ска­зав, что живёт в де­ся­том подъ­ез­де в квар­ти­ре № 333, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом де­вя­ти­этаж­ный. На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)
Ответ: 3

Тре­нер по­со­ве­то­вал Ан­дрею в пер­вый день за­ня­тий про­ве­сти на бе­го­вой до­рож­ке 15 минут, а на каж­дом сле­ду­ю­щем за­ня­тии уве­ли­чи­вать время, про­ведённое на бе­го­вой до­рож­ке, на 7 минут. За сколь­ко за­ня­тий Ан­дрей про­ведёт на бе­го­вой до­рож­ке в общей слож­но­сти 2 часа 25 минут, если будет сле­до­вать со­ве­там тре­не­ра?
Ответ: 5

Врач про­пи­сал па­ци­ен­ту при­ни­мать ле­кар­ство по такой схеме: в пер­вый день он дол­жен при­нять 3 капли, а в каж­дый сле­ду­ю­щий день — на 3 капли боль­ше, чем в преды­ду­щий. При­няв 30 ка­пель, он ещё 3 дня пьёт по 30 ка­пель ле­кар­ства, а потом еже­днев­но умень­ша­ет приём на 3 капли. Сколь­ко пу­зырь­ков ле­кар­ства нужно ку­пить па­ци­ен­ту на весь курс приёма, если в каж­дом со­дер­жит­ся 20 мл ле­кар­ства (что со­став­ля­ет 250 ка­пель)?
Ответ: 2

Врач про­пи­сал па­ци­ен­ту при­ни­мать ле­кар­ство по такой схеме: в пер­вый день он дол­жен при­нять 20 ка­пель, а в каж­дый сле­ду­ю­щий день — на 3 капли боль­ше, чем в преды­ду­щий. После 15 дней приёма па­ци­ент де­ла­ет пе­ре­рыв в 3 дня и про­дол­жа­ет при­ни­мать ле­кар­ство по об­рат­ной схеме: в 19-й день он при­ни­ма­ет столь­ко же ка­пель, сколь­ко и в 15-й день, а затем еже­днев­но умень­ша­ет дозу на 3 капли, пока до­зи­ров­ка не ста­нет мень­ше 3 ка­пель в день. Сколь­ко пу­зырь­ков ле­кар­ства нужно ку­пить па­ци­ен­ту на весь курс приёма, если в каж­дом со­дер­жит­ся 200 ка­пель?
Ответ: 7

Про­из­ве­де­ние де­ся­ти иду­щих под­ряд чисел раз­де­ли­ли на 7. Чему может быть равен оста­ток?
Ответ: 0

Сколь­ки­ми спо­со­ба­ми можно по­ста­вить в ряд два оди­на­ко­вых крас­ных ку­би­ка, три оди­на­ко­вых зелёных ку­би­ка и один синий кубик?
Ответ: 60

В бак объёмом 38 лит­ров каж­дый час, на­чи­ная с 12 часов, на­ли­ва­ют пол­ное ведро воды объёмом 8 лит­ров. Но в днище бака есть не­боль­шая щель, и из неё за час вы­те­ка­ет 3 литра. В какой мо­мент вре­ме­ни (в часах) бак будет за­пол­нен пол­но­стью.
Ответ: 18

Какое наи­мень­шее число иду­щих под­ряд чисел нужно взять, чтобы их про­из­ве­де­ние де­ли­лось на 7?
Ответ: 2

В ре­зуль­та­те па­вод­ка кот­ло­ван за­пол­нил­ся водой до уров­ня 2 метра. Стро­и­тель­ная помпа не­пре­рыв­но от­ка­чи­ва­ет воду, по­ни­жая её уро­вень на 20 см в час. Под­поч­вен­ные воды, на­о­бо­рот, по­вы­ша­ют уро­вень воды в кот­ло­ва­не на 5 см в час. За сколь­ко часов ра­бо­ты помпы уро­вень воды в кот­ло­ва­не опу­стит­ся до 80 см?
Ответ: 8

В меню ре­сто­ра­на име­ет­ся 6 видов са­ла­тов, 3 вида пер­вых блюд, 5 видов вто­рых блюд и 4 вида де­сер­та. Сколь­ко ва­ри­ан­тов обеда из са­ла­та, пер­во­го, вто­ро­го и де­сер­та могут вы­брать по­се­ти­те­ли этого ре­сто­ра­на?
Ответ: 360

Нефтяная компания бурит скважину для добычи нефти, которая залегает, по данным геологораз-ведки, на глубине 3 км. В течение рабочего дня бурильщики проходят 300 метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на 30 метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?

Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 9?

В обменном пункте можно совершить одну из двух операций:

• за 2 золотых монеты получить 3 серебряных и одну медную;
• за 5 серебряных монет получить 3 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебря-ных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько умень-шилось количество серебряных монет у Николая?

На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько ча-стей проведённые линии разделили поверхность глобуса?

Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.

В корзине лежит 50 грибов: рыжики и грузди. Известно, что среди любых 28 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько груздей в корзине?

Группа туристов преодолела горный перевал. Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний ки-лометр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине тури-сты начали спуск, который был более пологим.

Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут.

На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 35 км, между A и C — 20 км, между C и D — 20 км, между D и A — 30 км (все расстояния измеря-ются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C. Ответ дайте в километрах.

На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 50 км, между A и C — 40 км, между C и D — 25 км, между D и A — 35 км (все расстояния измеря-ются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C.

В классе учится 25 учащихся. Несколько из них ходили в кино, 18 человек ходили в театр, причём и в кино, и в театр ходили 12 человек. Известно, что трое не ходили ни в кино, ни в театр. Сколько человек из класса ходили в кино?

По эмпирическому закону Мура среднее число транзисторов на микросхемах каждый год удваи-вается. Известно, что в 2005 году среднее число транзисторов на микросхеме равнялось 520 млн. Определите, сколько в среднем миллионов транзисторов было на микросхеме в 2003 году.

В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколь-ко мест в восьмом ряду?

На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 5 кусков, если по жёлтым — 7 кусков, а если по зелёным — 11 кус-ков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?

В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано 10 холодильников, и в три последующих месяца продавали по 10 холодильников. С мая продажи увеличивались на 15 единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на 15 холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год?

В обменном пункте можно совершить одну из двух операций:

1) за 3 золотых монеты получить 4 серебряных и одну медную;

2) за 6 серебряных монет получить 4 золотых и одну медную.

У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 35 медных. На сколько уменьшилось коли-чество серебряных монет у Николы?

Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.)

Во всех подъездах дома одинаковое число этажей, а на каждом этаже одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 110 квартир?

Предыдущие статьи

Источник: testowik.ru