Фотоэффект — это явление, при котором из металлической пластины, облучаемой свет с определённой энергией, вылетают электроны.
Физика этого процесса оказалось достаточно простой. В металле всегда находятся свободные электроны, которые могут свободно перемещаться внутри металла. Когда на металл падает фотон с энергией (E = text) , эта энергия тратится на то, чтобы достать электрон из глубины металла, и чтобы передать ему некоторую кинетическую энергию. Энергия, которая тратится на то, чтобы достать электрон из металла, называется работой выхода.
Работа выхода — это характеристика поверхности материала. Она не зависит от света, от его частоты или интенсивности.
Из закона сохранения энергия следует очень важной формулой, называемой формулой Эйнштейна для фотоэффекта. Эта формула имеет вид: (text = A + E) , где: h — постоянная Планка, равная (6,6 bullet 10^) [Дж·с] v — частота света [Гц] А — работа выхода [Дж] Е — кинетическая энергия [Дж] Как было сказано в начале, только фотоны с определённой энергией могут выбить электрон из металла. Дело в том, что сначала энергия тратится на совершение работы (на доставание электрона из металла) и только потом на его разгон (кинетическую энергию). Поэтому, существует какое-то предельное значение частоты света, при которой происходит фотоэффект. Это то значение частоты, при которой энергии фотона хватает только на то, чтобы вытащить электрон из металла (совершить работу выхода), при этом на кинетическую энергию энергии фотона уже не хватает.
38 — ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ ФОТОНОВ / EMISSION AND ABSORPTION OF PHOTONS
Частота, при которой фотоэффект прекращается, называется красной границей фотоэффекта: (hv_ красная \ граница \ end> = А) , где: h — постоянная Планка, равная (6,6 bullet 10^) [Дж·с] (v_ красная \ граница \ end>) — частота света [Гц] А — работа выхода [Дж]
Важно заметить, что может наступить ситуация, когда фотон не выбил электрон (если его частота меньше либо равна частоте красной границы). Но не может наступить ситуации, когда фотон выбивает 2 и более электронов. Даже самые энергичные фотоны могут выбивать только 1 электрон. Поэтому справедливо заметить, что Nфотонов ≥ Nэлектронов График зависимости кинетической энергии вылетающих электронов от частоты падающих фотонов
Запирающее напряжение ― это напряжение, не позволяющее электронам покинуть фотокатод.
Если напряжение в цепи больше или равно запирающему напряжению, то электроны не могут достигнуть анода: даже если они покидают ненадолго фотокатод, сила электрического поля возвращает их в металл ― и фототока в цепи нет.
Запирающее напряжение определяется выражением (eU_ <зап>= Е_) , где e ― заряд электрона равный (1,6 bullet 10^) [Кл] (U_<зап >) ― запирающее напряжение [В] (Е_) ― кинетическая энергия фотоэлектрона [Дж]
Когда напряжение в цепи равно нулю (U = 0) , а фотокатод облучается светом достаточной энергии, чтоб создавать фотоэффект, ― в сети есть ток, его вызывают выбиваемые светом электроны. Когда напряжение в цепи равно запирающему напряжению (U = U_<з>) ― сила тока становится равной нулю, т. к. фототок прекращается.
Интерференция одиночных фотонов [Veritasium]
Как видно из формулы, запирающее напряжение зависит только от кинетической энергии электронов, которая, в свою очередь, зависит от частоты света (но не интенсивности) и работы выхода.
Интенсивность светового потока — это количество фотонов, падающих на пластину в единицу времени.
- Чем выше интенсивность, тем выше значение фототока насыщения.
- Чем ниже интенсивность, тем ниже значение фототока насыщения.
Однако, если частота света меньше либо равна частоте красной границы, фотоэффекта не произойдет независимо от интенсивности светового потока.
При необходимости найти энергию всего светопотока, достигающего пластины за 1 с, достаточно умножить энергию одного фотона на их количество: (sum E = hv bullet N_<фотонов>) , где:
(sum E) — энергия светопотока, достигшего пластину за 1 с [Дж]
h — постоянная Планка, равная 6,6 · 10 -34 [Дж · с]
(N_) — количество фотонов, достигающих пластину за 1 с
Источник: maximumtest.ru
Фотоэлектрический эффект
Выбивание светом электронов с поверхности токопроводящих материалов — явление, широко используемое сегодня в повседневной жизни. Например, некоторые системы сигнализации работают за счет передачи видимых или инфракрасных световых лучей на фотоэлектрический элемент, из которого выбиваются электроны, обеспечивающие электропроводность цепи, в которую он включен. Если на пути светового луча появляется препятствие, свет на датчик поступать перестает, поток электронов прекращается, цепь разрывается — и срабатывает электронная сигнализация.
Это явление, получившее название фотоэлектрического эффекта, или, кратко, фотоэффекта, было открыто в конце XIX столетия и сразу поставило целый ряд фундаментальных вопросов, поскольку ничего из того, что было известно ученым о строении металлов или природе света, фотоэффекта не объясняло. Нельзя сказать, что классическая теория запрещала бы свету выбивать электроны из металла.
Электромагнитные волны, по идее, могли «вымывать» электроны из металла подобно тому, как морские волны выносят на поверхность и постепенно прибивают к берегу легкие пробковые крошки. Однако проблема состояла в том, что столь простым объяснением в случае фотоэффекта ограничиться было невозможно. Во-первых, электроны появлялись практически мгновенно после начала облучения. Во-вторых, фотоэффект, как оказалось, возникал даже под воздействием самых слабых световых лучей, причем по мере повышения интенсивности облучения энергия высвобождаемых электронов не изменялась. И то, и другое вступало в явное противоречие с классической картиной взаимодействия света с электронами.
Проблему в конце концов удалось решить в начале ХХ века Альберту Эйнштейну, причем сделанные им выводы дали мощный толчок развитию квантовой механики. Незадолго до этого Макс Планк показал, что излучение черного тела можно адекватно описать, приняв за допущение, что атомы излучают и поглощают свет фиксированными энергетическими порциями — квантами.
Он полагал, что этот феномен каким-то образом обусловлен внутренним строением атомов, но отнюдь не природой света. Однако Эйнштейн воспринял идею Планка гораздо серьезнее и постулировал, что сам свет распространяется дискретными пучками энергии, которые он назвал фотонами. Иногда фотоны ведут себя подобно частицам, иногда — подобно волнам (см. Принцип дополнительности).
В частности, при взаимодействии с электроном фотон может вести себя как частица, и буквально выбивать электрон из атома (это соударение фотона с атомом можно уподобить столкновению двух бильярдных шаров). Причем для выбивания электрона при таком соударении достаточно единственного фотона. Далее, повышение интенсивности света приводит к увеличению числа фотонов (и, следовательно, числа выбитых электронов), но не энергии отдельно взятого фотона. Следовательно, и энергия, и скорость отдельно взятого выбитого фотоэлектрона не зависят от интенсивности света — но только от его частоты.
Рассуждая таким образом, Эйнштейн вывел следующее простое уравнение для описание энергии фотоэлектронов:
E = hν — φ
где ν — частота падающего света, h — постоянная Планка, а φ — так называемая «работа выхода», то есть минимальная энергия, необходимая для того, чтобы выбить электрон из атома металла.
Открытие электрона
Показать комментарии (2)
Свернуть комментарии (2)
1234 19.03.2008 22:17 Ответить
\Выбивание светом электронов с поверхности токопроводящих материалов — явление, широко используемое сегодня в повседневной жизни. Например, некоторые системы сигнализации работают за счет передачи видимых или инфракрасных световых лучей на фотоэлектрический элемент, из которого выбиваются электроны, обеспечивающие электропроводность цепи, в которую он включен. Если на пути светового луча появляется препятствие, свет на датчик поступать перестает, поток электронов прекращается, цепь разрывается — и срабатывает электронная сигнализация.\
Шибко умный физик написал, — всплакнулось.
derevo  1234
1234  16.11.2012
16.11.2012  14:58 Ответить
14:58 Ответить
УДИВИТЕЛЬНЫЕ ЗАКОНОМЕРНОСТИ ФОТОЭФФЕКТА НАХОДЯТ СВОЕ ПОЛНОЕ ОБЪЯСНЕНИЕ В РАМКАХ КЛАССИЧЕСКОЙ СТАТИСТИЧЕСКОЙ ФИЗИКИ (Статистической Оптики).
Наиболее интересным свойством фотоэффекта является тот факт, что энергия выбитых из фотокатода фотоэлектронов строго пропорциональна частоте падающего на фотокатод света и не зависит от интенсивности света.
Этот закон фотоэффекта был открыт Филиппом Ленардом в 1902 году экспериментальным путем и не нашел до последнего времени своего должного теоретического объяснения.
Особенно поразительно этот эффект проявляется в полупроводниковых детекторах излучений, амплитудное разрешение которых составляет единицы, а порой и доли процентов. На выходе таких детекторов получаются очень узкие амплитудные пики с высоким разрешением (на амплитудных анализаторах спектров).
Создается такое впечатление, как будто что-то вылетело из излучателя со строго определенной энергией и полностью передалось со всей своей энергией отдельному электрону атома фотоприемника. При этом данный эффект не зависит от расстояния между излучателем и приемником.
Как говорится, здесь есть от чего сойти с ума, что и сделали благополучно все корифеи физики ХХ века.
В результате всего этого были «изобретены» гипотетические фотоны, которые, якобы, и переносят эту энергию от излучателя к фотоприемнику.
При попытках объяснить фотоэффект, как правило, в ВУЗовских учебниках допускаются довольно грубые ошибки. Так, например, утверждается, что, якобы, согласно Классической физике при увеличении интенсивности падающего на фотокатод света должна увеличиваться энергия вылетающих фотоэлектронов, чего на самом деле не происходит.
Увеличивается лишь общее количество вылетающих фотоэлектронов, а распределение электронов по скоростям и энергиям остается прежним и не зависит от величины потока падающего на фотокатод света.
И, как результат подобных заблуждений, начинается выдумывание разных «квантовых диковинок» типа фотонов как некоторых сгустков энергии, которые, якобы, и бьют метко по электронам, выбивая их наружу. При первом же детальном анализе явления фотоэффекта подобные «истолкования» не выдерживают элементарной критики.
Сразу же следует сказать, что изобретатели «новых теорий», просто-напросто, не учитывают статистический характер света.
Из Статистической физики (со времен Молекулярной физики) хорошо известно, что функция распределения частиц по скоростям или энергиям не зависит от участвующих в процессе частиц. И чем больше частиц в этом процессе, тем с большой точностью выполняется данная закономерность.
Статистический характер световых полей обусловлен тем, что источники света обычно состоят из огромного числа хаотически расположенных в пространстве и не связанных между собой элементарных излучателей (атомы, молекулы), испускание света которыми имеет вероятностный характер. Поэтому рассмотрение данной задачи следует вести исключительно в рамках статистической физики и статистической оптики с использованием функций распределения электронов по скоростям или по энергиям.
Экспериментаторам, как правило, приходится иметь дело с веществами, которые состоят из огромного числа частиц (атомов или молекул), поэтому и статистические закономерности здесь выполняются с высокой точностью.
Рассмотрение этого сложного вопроса начинается с анализа энергетического распределения (функции распределения) фотоэлектронов, возникающих при облучении фотокатода светом определенного спектрального состава.
Источник: elementy.ru
Фотоэффект | теория по физике квантовая физика
Начало теории электромагнитной природы света заложил Максвелл, который заметил сходство в скоростях распространения электромагнитных и световых волн. Но согласно электродинамической теории Максвелла любое тело, излучающее электромагнитные волны, должно в итоге остынуть до абсолютного нуля. В действительности этого не происходит. Противоречия между теорией и опытными наблюдениями были разрешены в начале XX века, вскоре после того, как был открыт фотоэффект.
Что такое фотоэффект
Фотоэффект — испускание электронов из вещества под действием падающего на него света.

Явление фотоэффекта было открыто в 1887 году Генрихом Герцем. Фотоэффект также был подробно изучен русским физиком Александром Столетовым в период с 1888 до 1890 годы. Этому явлению он посвятил 6 научных работ.
Для наблюдения фотоэффекта нужно провести опыт. Для этого понадобится электрометр и подсоединенная к нему пластинка из цинка (см. рисунок ниже). Если дать пластинке положительный заряд, то при ее освещении электрической дугой скорость разрядки электрометра не изменится. Но если цинковую пластинку зарядить отрицательно, то свет от дуги заставить электрометр разрядиться очень быстро.
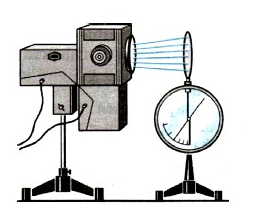
Наблюдаемое во время этого эксперимента явление имеет простое объяснение. Свет вырывает электроны с поверхности цинковой пластинки. Если она имеет отрицательный заряд, электроны отталкиваются от нее, что приводит к полному разряжению электрометра.
Причем при повышении интенсивности освещения скорость разрядки увеличивается, ровно, как и наоборот: при уменьшении интенсивности освещения электрометр разряжается медленно. Если же зарядить пластинку положительно, то электроны, которые вырываются светом, притягиваются к ней. Поэтому они оседают на ней, не изменяя заряд электрометра.
Если между световым пучком и отрицательно заряженной пластиной поставить лист стекла, пластинка перестанет терять электроны независимо от интенсивности излучения. Это связано с тем, что стекло задерживает ультрафиолетовое излучение. Отсюда можно сделать следующий вывод:
Явление фотоэффекта может вызвать только ультрафиолетовый участок спектра.
Волновая теория света не может объяснить, почему электроны могут вырываться только под действием ультрафиолета. Ведь даже при большой амплитуде и силе волн электроны остаются на месте, когда, казалось бы, они должны непременно быть вырванными.
Законы фотоэффекта
Чтобы получить более полное представление о фотоэффекте, выясним, от чего зависит количество электронов, вырванных светом с поверхности вещества, а также, от чего зависит их скорость, или кинетическая энергия. Выяснить все это нам помогут эксперименты.
Первый закон фотоэффекта
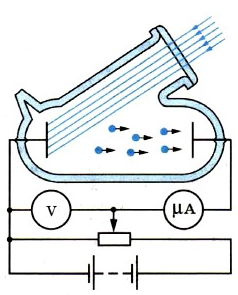
Возьмем стеклянный баллон и выкачаем из него воздух (смотрите рисунок выше). Затем поместим в него два электрода. На электроды подадим напряжение и будем регулировать его с помощью потенциометра и измерять при помощи вольтметра.
В верхней части нашего баллона есть небольшое кварцевое окошко, которое пропускает весь свет, в том числе ультрафиолетовый. Через него падает свет на один из электродов (в нашем случае на левый электрод, к которому присоединен отрицательный полюс батареи).
Мы увидим, что под действием света этот электрод начнет испускать электроны, которые при движении в электрическом поле будут создавать электрический ток. Вырванные электроны будут направляться ко второму электроду. Но если напряжение небольшое, второго электрода достигнут не все электроны.
Если интенсивность излучения сохранить, но увеличить между электродами разность потенциалов, то сила тока будет увеличиваться. Но как только она достигнет некоторого максимального значения, рост силы тока при дальнейшем увеличении напряжения прекратится. Максимальное значение силы тока будем называть током насыщения.
Ток насыщения — максимальное значение силы тока, также называемое предельным значением силы фототока.
Ток насыщения обозначается как I н . Единица измерения — А (Кл/с). Численно величина равна отношению суммарному заряду вырванных электронов в единицу времени:
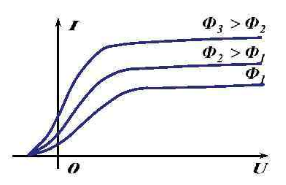
Если же мы начнем изменять интенсивность излучения, то сможем заметить, что фототок насыщения также начинается меняться. Если интенсивность излучения ослабить, максимальное значение силы тока уменьшится. Если интенсивность светового потока увеличить, ток насыщения примет большее значение. Отсюда можно сделать вывод, который называют первым законом фотоэффекта.
Первый закон фотоэффекта:
Число электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны. Иными словами, фототок насыщения прямо пропорционален падающему световому потоку Ф.
Второй закон фотоэффекта
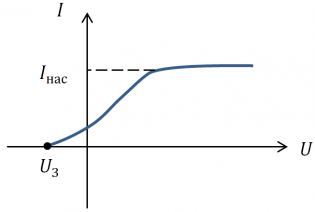
Теперь произведем измерения кинетической энергии, то есть, скорости вырывания электронов. Взгляните на график, представленный ниже. Видно, что сила фототока выше нуля даже при нулевом напряжении. Это говорит о том, что даже при нулевой разности потенциалов часть электронов достигает второго электрода.
Если мы поменяем полярность батареи, то будем наблюдать уменьшение силы тока. Если подать на электроды некоторое значение напряжения, равное U з , сила тока станет равно нулю. Это значит, что электрическое поле тормозит вырванные электроны, останавливает их, а затем возвращает на тот же электрод.
Напряжение, равное U з , называют задерживающим напряжением. Оно зависит зависит от максимальной кинетической энергии электронов, которые вырываются под действием света. Измеряя задерживающее напряжение и применяя теорему о кинетической, можно найти максимальное значение кинетической энергии электронов. Оно будет равно:
m v 2 2 . . = e U з
Опыт показывает, что при изменении интенсивности света (плотности потока излучения) задерживающее напряжение не меняется. Значит, не меняется кинетическая энергия электронов. С точки зрения волновой теории света этот факт непонятен.
Ведь чем больше интенсивность света, тем большие силы действуют на электроны со стороны электромагнитного поля световой волны и тем большая энергия, казалось бы, должна передаваться электронам. Но экспериментальным путем мы обнаруживаем, что кинетическая энергия вырываемых светом электронов зависит только от частоты света. Отсюда мы можем сделать вывод, являющийся вторым законом фотоэффекта.
Второй закон фотоэффекта:
Максимальная кинетическая энергия фотоэлектронов линейно растет с частотой света и не зависит от его интенсивности.
Причем, если частота света меньше определенной для данного вещества минимальной частоты νmin, фотоэффект наблюдаться не будет.
Теория фотоэффекта
Все попытки объяснить явление фотоэффекта электродинамической теорией Максвелла, согласно которой свет — это электромагнитная волна, непрерывно распределенная в пространстве, оказались тщетными. Нельзя было понять, почему энергия фотоэлектронов определяется только частотой света и почему свет способен вырывать электроны лишь при достаточно малой длине волны.
В попытках объяснить это явление физик Макс Планк предложил, что атомы испускают электромагнитную энергию отдельными порциями — квантами, или фотонами. И энергия каждой порции прямо пропорциональна частоте излучения:
h — коэффициент пропорциональности, который получил название постоянной Планка. Она равна 6,63∙10 –34 Дж∙с.
Пример №1. Определите энергию фотона, соответствующую длине волны λ = 5∙10 –7 м.
Энергия фотона равна:
Выразим частоту фотона через скорость света:
Идею Планка продолжил развивать Эйнштейн, которому удалось дать объяснение фотоэффекту в 1905 году. В экспериментальных законах фотоэффекта Эйнштейн увидел убедительное доказательство того, что свет имеет прерывистую структуру и поглощается отдельными порциями. Причем энергия Е каждой порции излучения, по его расчетам, полностью соответствовала гипотезе Планка.
Из того, что свет излучается порциями, еще не вытекает вывода о прерывистости структуры самого света. Ведь и воду продают в бутылках, но отсюда не следует, что вода состоит из неделимых частиц. Лишь фотоэффект позволил доказать прерывистую структуру света: излученная порция световой энергии Е = hν сохраняет свою индивидуальность и в дальнейшем. Поглотиться может только вся порция целиком.
Кинетическую энергию фотоэлектрона можно найти, используя закон сохранения энергии. Энергия порции света hν идет на совершение работы выхода А и на сообщение электрону кинетической энергии. Отсюда:
h ν = A + m v 2 2 . .
Работа выхода — минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Полученное выражение объясняет основные факты, касающиеся фотоэффекта. Интенсивность света, по Эйнштейну, пропорциональна числу квантов (порций) энергии hν в пучке света и поэтому определяет количество вырванных электронов. Скорость же электронов согласно зависит только от частоты света и работы выхода, которая определяется типом металла и состоянием его поверхности. От интенсивности освещения кинетическая энергия фотоэлектронов не зависит.
Для каждого вещества фотоэффект наблюдается лишь при освещении его светом с минимальной частотой волны νmin. Это объясняется тем, что для вырывания электрона без сообщения ему скорости нужно выполнять как минимум работу выхода. Поэтому энергия кванта должна быть больше этой работы:
Предельную частоту νmin называют красной границей фотоэффекта. При этой частоте фотоэффект уже наблюдается.
Красная граница фотоэффекта равна:
Минимальной частоте, при которой возможен фотоэффект для данного вещества, соответствует максимальная длина волны, которая также носит название красной границы фотоэффекта. Это такая длина волны, при которой фотоэффект еще наблюдается. Обозначается она как λmах или λкр.
Максимальная длина волны, при которой еще наблюдается фотоэффект, равна:
Работа выхода А определяется родом вещества. Поэтому и предельная частота vmin фотоэффекта (красная граница) для разных веществ различна. Отсюда вытекает еще один закон фотоэффекта.
Третий закон фотоэффекта:
Для каждого вещества существует максимальная длина волны, при которой фотоэффект еще наблюдается. При больших длинах волн фотоэффекта нет.
Вспомните опыт, который мы описали в самом начале. Когда между цинковой пластинкой и световым пучком мы поставили зеркало, фотоэффект был прекращен. Это связано с тем, что красная граница для цинка определяется величиной λmах = 3,7 ∙ 10 -7 м. Эта длина волны соответствует ультрафиолетовому излучению, которое не пропускало стекло.
Пример №2. Чему равна красная граница фотоэффекта νmin, если работа выхода электрона из металла равна A = 3,3∙10 –19 Дж?
Применим формулу для вычисления красной границы фотоэффекта:
Задание EF15717 При увеличении в 2 раза частоты света, падающего на поверхность металла, задерживающее напряжение для фотоэлектронов увеличилось в 3 раза. Первоначальная частота падающего света была равна 0,75 ⋅10 15 Гц. Какова длина волны, соответствующая «красной границе» фотоэффекта для этого металла? Ответ записать в нм.
Алгоритм решения
Источник: spadilo.ru