Из наличия у фотона импульса вытекает, что свет, падающий на поверхность тела, действует на это тело с какой – то силой. Сила светового давления F на поверхность равна произведению светового давления P на площадь S поверхности: F = P S . Световое давление – это давление, производимое светом при нормальном падении на поверхность, которое выражается соотношением P = E c e (1 + r ) или P = w (1 + r ) , где E e — плотность потока энергии излучения, падающего на поверхность (энер- гетическая освещенность поверхности), с — скорость света в вакууме, w = E c e – объемная плотность энергии излучения, r – коэффициент отражения. 61
Если свет падает на поверхность под углом α к нормали, то давление, производимое светом на поверхность, выражается соотношением P = E c e (1 + r )cos α . Для идеально отражающей (зеркальной) поверхности r = 1, для идеально поглощающей поверхности (абсолютно черное тело) r = 0. Энергетическая освещенность поверхности E e – это величина, численно равная мощности излучения, падающей на единичную площадку: E e = Ô S е , где Ф е — поток энергии (мощность) излучения, падающего на поверхность S .
[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]
5.5. Примеры решения задач
Задача №1. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ = 500 нм. Принимая Солнце за абсолютно черное тело, определить: 1) энергетическую светимость Солнца R ( T ), 2) поток мощности, излучаемый Солнцем Ф е , 3) массу m электромагнитных волн, излучаемых Солнцем за
| время t = 1 с. | Решение | ||||||
| Дано | |||||||
| λ = 500 нм, | 1. Энергетическая светимость черного тела выражается | ||||||
| m C =1,98·10 30 кг, | формулой Стефана–Больцмана R ( T ) = σ T 4 . | ||||||
| R C =6,95·10 8 м, | Температура излучающей поверхности может быть | ||||||
| t = 1 с | определена из закона смещения Вина: | ||||||
| R e = ?, | |||||||
| Ф е = ?, | λ max = | b | . | ||||
| m = ? | |||||||
| T | |||||||
| Выразив отсюда температуру Т и подставив в закон Стефана–Больцмана, | |||||||
| b | 4 | ||||||
| получим R ( T ) = σ | . Произведя вычисления, найдем R ( T )= 6,4·10 7 Вт/м 2 . | ||||||
| λ max | |||||||
2. Поток мощности Ф е , излучаемый Солнцем, равен произведению энер- гетической светимости тела на площадь его поверхности: Ф е = R ( T ) S = R ( T ) 4π r 2 , где r =7·10 8 м — радиус Солнца. Ф е = 4·3,14(7·10 8 ) 2 6,4·10 7 = 3,9·10 26 Вт. 3. Массу электромагнитных волн всех длин, излучаемых Солнцем за вре- мя t =1 с, определим, применив закон взаимосвязи массы и энергии: E = m с 2 . С другой стороны, энергия излучаемых электромагнитных волн равна произведению потока энергии на время излучения: E = Ф е t. Приравняв выражения для энергии, получим, что 62
m = Ф c 2 e t . Подставив числовые значения, получим m = 4·10 9 кг. Задача №2. Определить максимальную кинетическую энергию и скорость фотоэлектронов, выбитых с поверхности натрия светом с длиной волны λ для
РЕЗОНАНС НАПРЯЖЕНИЙ. Решение задачи 5.113
| двух случаев: 1) λ 1 = 410 нм, 2) λ 2 = 550 нм. | Решение | |||||||||
| Дано | ||||||||||
| А вых = 2,28 эВ, | 1. Длина волны падающего света λ 1 = 410 нм. Энергия | |||||||||
| e = 1,6 · 10 -19 Кл, | фотона вычисляется по формуле | |||||||||
| m e = 9,1 · 10 -31 кг, | h ν = | hc | ||||||||
| λ 1 = 410 нм, | . | |||||||||
| λ | 1 | |||||||||
| λ 2 = 550 нм, | ||||||||||
| Подставив числовые значения, получим h ν = 4,85 · 10 -19 Дж= | ||||||||||
| 1эВ=1,6 · 10 -19 Дж | = 3,03 эВ. | |||||||||
| E кин = ?, | ||||||||||
| Из уравнения Эйнштейна находим | ||||||||||
| V = ? | E | = | m V | 2 | = h ν− A | = 3,03 эВ – 2,28 эВ = 0,75 эВ. | ||||
| кин | max | |||||||||
| 2 | вых | |||||||||
| Полученная | энергия фотоэлектрона (0,75 эВ) много меньше энергии по- | |||||||||
коя электрона (0,5 МэВ). Следовательно, для данного случая максимальная кинетическая энергия фотоэлектрона может быть вычислена по классической
| формуле E | кин | = | mV max 2 | . E | = 0,75 эВ = 1,2 · 10 -19 Дж. |
| 2 | кин | ||||
Скорость фотоэлектрона, выбитого с поверхности натрия, найдем по формуле
| V = | 2 E кин | . Выполнив вычисления, получим V =5,1 · 10 5 м/с. |
| m e | ||
| 2. Длина волны падающего света λ 2 = 550 нм. Энергия падающего фотона | ||
h ν = hc . λ 2 Подставив числовые значения, получим h ν = 3,61 · 10 -19 Дж = 2,26 эВ. Полученное значение меньше работы выхода фотоэлектрона с поверхности натрия, поэтому фотоэффект при падении света с λ 2 = 550 нм наблюдаться не будет. Задача №3. Красная граница фотоэффекта для некоторого металла равна λ 0 = 550 нм. Определить: 1) работу выхода А вых фотоэлектронов из этого металла; 2) максимальную скорость фотоэлектронов, вырываемых с поверхности
| металла светом с длиной волны λ = 400 нм. | ||||||||||||
| Дано | Решение | |||||||||||
| e = 1,6 · 10 -19 Кл, | 1. Из определения «красной границы» фотоэффекта | |||||||||||
| m e = 9,1 · 10 -31 кг, | A | c | hc | |||||||||
| λ 0 = 550 нм, | ν | = | вых | или λ | = | = | ||||||
| h | ν 0 | A вых | ||||||||||
| λ = 400 нм, | получаем формулу для расчета работы выхода | |||||||||||
| 1 эВ=1,6 · 10 -19 Дж | ||||||||||||
63
| А вых = ?, | A вых = | hc | . | |
| V = ? | λ | |||
Подставив числовые значения, получим А вых = 3,61 · 10 -19 Дж = 2,26 эВ. 2. Для вычисления максимальной скорости фотоэлектронов, вырываемых с поверхности металла светом, воспользуемся уравнением Эйнштейна в виде
hc = hc λ λ 0 Из него получим V = 2 hc m
+ m V max 2 . 2
| 1 | 1 | |
| − | . | |
| λ | λ 0 | |
Выполнив вычисления, получим V = 5,45·10 5 м/с. Задача №4. Задерживающее напряжение U з для платиновой пластинки составляет 3,7 В. При тех же условиях для другой пластинки задерживающее напряжение равно 5,3 В. Определить работу выхода фотоэлектронов из второй
| пластинки, если для платины А вых1 = 6,3 эВ . | ||||
| Дано | Решение | |||
| А вых1 = 6,3 эВ, | Зная задерживающее напряжение U з , можно определить | |||
| e = 1,6 · 10 -19 Кл, | максимальное значение кинетической энергии фотоэлектро- | |||
| U з1 = 3,7 В, | нов: | mV 2 | ||
| U з2 = 5,3 В, | ||||
| 1 эВ=1,6 · 10 | -19 | eU З = | max | . |
| 2 | ||||
| Дж | ||||
| Уравнение Эйнштейна тогда примет вид | ||||
| А вых2 = ? | ||||
| h ν = A вых + eU з . | ||||
Запишем его для каждой пластинки: h ν = A вых1 + eU з 1 , h ν = A вых2 + eU з 2 . Выражая из них работу выхода фотоэлектронов из второй пластинки А вых2 , получим А вых2 = А вых1 + е ( U з1 — U з2 ). Подставив числовые значения, найдем А вых2 = 4,7 эВ . Задача №5. Параллельный пучок света длиной волны λ = 500 нм падает нормально на зачерненную поверхность, производя давление Р = 10 мкПа. Определить: 1) концентрацию n фотонов в потоке; 2) число фотонов N , падающих на поверхность площадью 1 м 2 за время 1 с.
| Дано | Решение | ||||
| λ = 500 нм, | 1. Концентрация n фотонов в пучке может быть найдена как | ||||
| Р = 10 мкПа, | n = | w | , | ||
| S = 1 м 2 , | |||||
| ε | |||||
| t = 1 с | |||||
| 64 | |||||
Источник: studfile.net
Задерживающее напряжение для серебряной пластинки составляет 5 в при тех же условиях
Практический курс физики
Задерживающее напряжение для платиновой пластинки (работа выхода 6,3 эВ) составляет 3,7 В. При тех же условиях для другой пластинки задерживающее напряжение равно 5,3 В. Определите работу выхода электронов из этой пластинки.
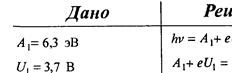 |
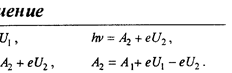 |
 |
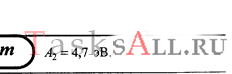 |
Источник: tasksall.ru
Задерживающее напряжение для серебряной пластинки (работа выхода 4,7 эВ) составляет 5,3 В. При тех же условиях для платиновой пластинки
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
- Обратная связь
- Правила сайта
Источник: www.soloby.ru