Как следует из решения уравнения Шредингера для атома водорода, квантовое состояние электрона в этом атоме (можно сказать и квантовое состояние атома) полностью определяется заданием трех квантовых чисел. Каждое из квантовых чисел принимает только целочисленные значения и определяет, то есть предсказывает результаты измерения основных физических величин в заданном квантовом состоянии атома.
1. Главное квантовое число . Это квантовое число принимает значения
и определяет полную энергию электрона в любом квантовом состоянии
Можно отметить, что эти значения энергии являются собственными значениями гамильтониана в уравнении Шредингера для водородоподобного атома. Поэтому в связанном состоянии электрон в атоме водорода имеет дискретный энергетический спектр, лежащий в области отрицательных значений и имеющий точку сгущения .
2. Орбитальное (азимутальное) квантовое число . В квантовых состояниях с заданным значением главного квантового числа азимутальное квантовое число может иметь следующие значения:
5.1 Квантовые числа
Стационарные волновые функции , описывающие различные квантовые состояния атома, являются собственными функциями не только оператора полной энергии , но и оператора квадрата момента импульса , причем
Следовательно, в любом квантовом состоянии атом обладает определенным значением квадрата момента импульса, причем модуль орбитального момента импульса движущегося в атоме электрона однозначно определяется орбитальным квантовым числом:
Проанализируем эту формулу квантования момента импульса. Сравнивая ее с условием квантования момента импульса движущегося электрона в теории Бора (3-й постулат Бора). Можно заметить, что эти условия не совпадают. И дело не только в отличии числовых значений, рассчитанных по этим формулам. Принципиальное отличие этих соотношений состоит в том, что в квантовой механике возможны состояния атома с нулевым моментом импульса. Во всех -состояниях и, частности, в основном -состоянии, когда , по формуле получаем .
При классическом описании движения электрона в атоме по определенной траектории (орбите) в любом состоянии атом должен обладать ненулевым моментом импульса.
Опыт подтверждает существование квантовых состояний атома с нулевыми орбитальными моментами. Следовательно, опыт подтверждает, что только отказ от классического траекторного способа описания движения электрона в атоме позволяет правильно рассчитать и предсказать свойства атома. Вероятностный способ описания движения частиц в квантовой механике является единственно правильным способом описания свойств атомных систем — таков вывод современной физики.
Так как движущийся вокруг ядра электрон является заряженной частицей, то такое движение обуславливает протекание некоторого замкнутого тока в атоме, который можно охарактеризовать орбитальным магнитным моментом .
В теории Бора, когда с позиции классической теории рассматривается круговое движение электрона по орбите радиуса со скоростью , величина орбитального механического момента равна . Если время полного оборота электрона Т, то такому движению соответствует замкнутый ток
Квантовые числа. 1 часть. 10 класс.
который можно охарактеризовать величиной магнитного момента
Связь механического и магнитного моментов при этом определяется гиромагнитным отношением
Так как заряд электрона отрицателен, то для орбитального движения направление вектора магнитного момента противоположно направлению вектора механического момента импульса (рис. 1).
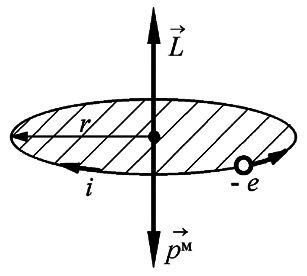
Итак, в любом квантовом состоянии атом водорода обладает не только механическим моментом , но и магнитным моментом.
Здесь универсальная постоянная
служит единицей измерения магнитных моментов атомов и называется магнетоном Бора.
Если атом переходит из одного квантового состояния в другое с испусканием (поглощением) фотона излучения, то возможны лишь такие переходы, для которых орбитальное квантовое число изменяется на единицу. Это правило, согласно которому для оптических переходов , называется правилом отбора. Наличие такого правила отбора обусловлено тем, что электромагнитное излучение (фотон) уносит или вносит не только квант энергии, но и вполне определенный момент импульса, изменяющий орбитальное квантовое число для электрона всегда на единицу.
3. Магнитное квантовое число . В квантовом состоянии с заданным значением орбитального квантового числа , магнитное квантовое число может принимать различных значений из ряда
Физический смысл магнитного квантового числа вытекает из того, что волновая функция , описывающая квантовое состояние электрона в атоме водорода, является собственной функцией оператора проекции момента импульса , причем
Поэтому, из общих положений квантовой механики следует, что проекция момента импульса электрона на выделенное в пространстве направление может иметь только определенные значения, равные
Направление в пространстве обычно выделяется внешним полем (например, магнитным или электрическим), в котором находится атом.
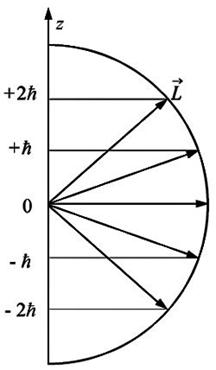
Так как формула квантования проекции механического момента соответствует вполне определенным направлениям ориентации в пространстве вектора (рис. 2), то эту формулу называют обычно формулой пространственного квантования.
С точки зрения классического представления об электронной орбите, с учетом перпендикулярности вектора к плоскости орбиты, соотношение определяет возможные дискретные расположения электронных орбит в пространстве по отношению к направлению внешнего поля.
Отмеченная выше связь механического и магнитного моментов атома позволяет с учетом записать также возможные значения проекции магнитного момента атома на выделенное направление :
зависящие от значения магнитного квантового числа .
4. Спин электрона.
Из квантовой теории следует, что вследствие симметрии электронного «облака» механический и магнитный моменты атома, находящегося в основном, невозбужденном состоянии, равны нулю. Следовательно, если в опыте Штерна — Герлаха обеспечить условия, при которых в атомном пучке будут двигаться невозбужденные атомы, то такой атомный пучок не должен расщепляться магнитным полем. Поэтому на стеклянной пластинке мы увидели бы в центре одну узкую зеркальную полоску.
Однако, эксперимент не подтвердил такой вывод квантовой теории. Пучок невозбужденных атомов серебра расщепился на два пучка, которые напылили на стеклянной пластинке две узкие зеркальные полоски, сдвинутые симметрично вверх и вниз. Измерение этих сдвигов позволило определить магнитный момент невозбужденного атома серебра. Его проекция на направление магнитного поля оказалась равной или .
Это противоречие квантовой теории и опыта было не единственным, обнаруженным к этому времени в различных экспериментах. Все эти трудности квантовой теории были преодолены, когда в 1925 г. С.Гаудсмит и Дж.Уленбек выдвинули смелую теорию о том, что сам электрон является носителем «собственных» механического и магнитного моментов, не связанных с движением электрона в пространстве. Эта гипотеза получила название гипотезы о спине электрона.
Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Однако, такая модель вращающегося заряженного шарика оказалась несостоятельной. Прежде всего, расчет показал, что ни при каких допустимых (т.е. меньше скорости света) скоростях нельзя вращением электрона индуцировать магнитный момент, равный по величине магнетону Бора. Кроме того, величина гиромагнитного отношения собственного магнитного и механического моментов, рассчитанная для модели вращающегося электрона, оказалась в два раза меньше, чем получаемая в опытах.
Модель электрона, вращающегося вокруг своей оси, как вращается Земля, двигаясь по околосолнечной орбите, в настоящее время может использоваться только при популярном изложении свойств атома.
Спин электрона не имеет классического аналога. Он характеризует внутреннее свойство квантовой частицы, связанное с наличием у нее дополнительной степени свободы. Количественная характеристика этой степени свободы — спин является для электрона такой же величиной как, например, его масса и заряд .
При согласовании теории и эксперимента Гаудсмит и Уленбек, по аналогии с орбитальными моментами, предположили, что величины собственных механического и магнитного моментов электрона определяются формулами
Проекции собственных моментов на выделенное направление в такой теории определяются спиновым квантовым числом . При этом
Величина спиновых моментов электрона постоянна, а с дополнительной степенью свободы электрона связаны -проекции этих моментов, которые определяются спиновым квантовым числом и принимают два значения. О таких двух квантовых состояниях обычно говорят как о состояниях со спином, направленным вверх или вниз . Поэтому, определяя квантовое состояние электрона в любой системе следует указать также и ориентацию спина.
Источник: studopedia.su
Квантовые числа
Согласно атомной модели Нильса Бора, протоны и нейтроны атома находятся в ядре, а электроны — вокруг него. Хотя мы не можем знать, где именно находится электрон, есть области, где он, скорее всего, может быть обнаружен, — атомные орбитали. И как мы можем определить эти орбитали? Очень просто, используя квантовые числа.

Какие квантовые числа?
Есть 4 квантовых числа. Три из них дают нам информацию о том, где находится электрон определенного атома, то есть они дают нам информацию об орбитали. С другой стороны, четвертое квантовое число говорит нам не о том, где находится электрон, а о том, как это сделать. Вы все еще не очень понимаете это? Действуй!
- Главное квантовое число (п). Это последний энергетический уровень, который необходимо заполнить, и он указывает размер орбитали и, следовательно, расстояние между ядром и электроном. Почему? Очень просто. Чем больше орбиталь, тем дальше электрон может быть от ядра атома.
- Азимутальное или вторичное квантовое число (л). Укажите форму орбиты.
- Магнитное квантовое число (м). Указывает ориентацию орбиты.
- Спиновое квантовое число (s). Скажите, в какую сторону вращается электрон.
Легко, правда? Пойдем с важным!
Как получаются квантовые числа
Чтобы получить квантовые числа, вам просто нужно выполнить 2 простых шага:
- Напишите электронную конфигурацию.
- Получите квантовые числа от дифференциального электрона (последнего, заполняющего орбиталь).
Электронная конфигурация
Начнем с шага 1, запишем электронную конфигурацию. Как? Есть два способа сделать это, давайте перейдем к делу!
Диаграмма Меллера
Этот метод указывает порядок заполнения орбиталей с помощью следующего рисунка:
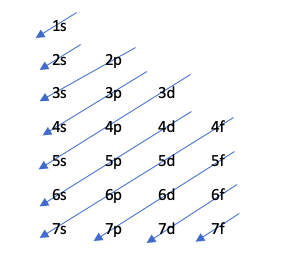
Эта диаграмма подчиняется принципу Ауфбау, который утверждает, что орбитали заполняются в порядке возрастания энергии, то есть орбиталь с наименьшей энергией заполняется раньше.
Чтобы узнать, какая орбиталь имеет больше энергии, выполняется операция n + l. Если эта операция для двух разных атомов приводит к одному и тому же числу, тот, у которого номер n больше, будет иметь больше энергии. Другими словами, в случае ничьей первым заполняется тот, у кого наименьший номер n. Посмотрим на это на примере:
4р: п + 4 -> 1 + 5 = XNUMX
5с: n + l -> 5 + 0 = 5
Поскольку в правиле n + l есть ничья, оно заполняет 4p раньше, потому что его номер n меньше.
Модель ядра
Чтобы получить электронную конфигурацию, соответствующую этой модели, вы должны очень хорошо знать таблицу Менделеева. Если у нас есть атомный номер и положение элемента в таблице, это совсем несложно!
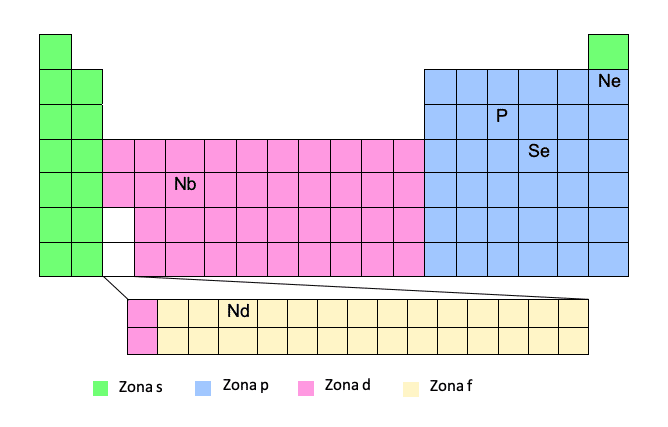
Этот метод считается упрощенным, поскольку он позволяет не записывать полную электронную конфигурацию. Таким образом, мы можем записать название благородного газа выше в скобках, а затем путь от этого благородного газа до рассматриваемого элемента. Посмотрим на пример: Таким образом, мы запишем траекторию с учетом номера периода (строки периодической таблицы) и «зоны» и, как только электронная конфигурация будет написана, мы извлечем квантовые числа.
Люминофор (P) будет записан из предыдущего благородного газа, то есть неона:
P -> [Ne] 3 с 2 3p 3
Конечно, с этим методом нужно быть осторожным, так как зоны d и f — особые зоны. Во время путешествия в зону d мы будем ставить не номер периода (строки), а номер периода минус один. То же самое и с областью F, мы будем ставить не номер периода, а номер периода минус два. Вы поймете это лучше на нескольких примерах:
Nb -> [Kr] 5s 1 4d 4
Хотя это период 5, когда мы находимся в зоне d, мы вычитаем 1.
Nd -> [Xe] 6s 2 4f 14
Хотя это период 6, когда мы находимся в зоне f, мы вычитаем 2.
Исключения в электронной конфигурации
Электронная конфигурация имеет несколько особенностей, которые, если вы не знаете о них, могут привести к большим головным фидерам. Но не паникуйте! Мы вам расскажем!
Зона F
Зона F появляется в нижней части таблицы Менделеева, но на самом деле она «встроена» в промежуток, который мы видим белым, то есть между первым и вторым элементами двух последних строк зоны D.
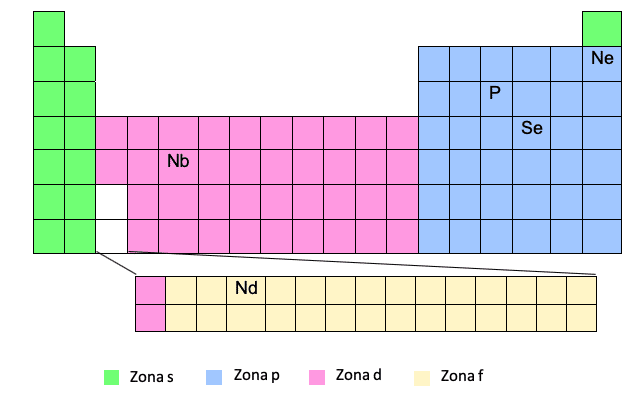
Ты видишь это? По этой причине иногда, когда нам нужно записать электронную конфигурацию элемента в зоне F, например, Nd, нам придется поместить электрон в зону D соответствующего уровня относительно того элемента в зоне D, который является перед входом в зону F.
Ce -> [Xe] 6s 2 5d 1 4f 1
Группа 6 и Группа 11
Переходные металлы группы 6 и группы 11 имеют 4 и 9 электронов на последних оболочках соответственно. Следовательно, чтобы быть более стабильным элементом, s-орбиталь возбуждается и теряет электрон, который переходит на следующую орбиталь, d. Таким образом, на s-орбитали останется электрон; и d с 5, если это элемент группы 6, или с 10, если это элемент группы 11.
Ag -> [Kr] 5s 2 4d 9
По-видимому, это была бы электронная конфигурация серебра (Ag). Однако потеря электрона с s-орбитали выглядит так:
Ag -> [Kr] 5s 1 4d 10
Однако есть исключения из этого правила, такие как вольфрам (группа 6), у которого остается 2 электрона на s-орбитали и 4 электрона на d-орбитали.
Но не волнуйтесь! Наиболее типичные из них (Cr, Cu, Ag и Au) подчиняются этому правилу.
Ты понял? Хорошо. Это все, что вам нужно знать об электронной конфигурации. Пойдем за квантовыми числами!
Как получить квантовые числа
Чтобы получить квантовые числа, мы должны знать, сколько электронов помещается на каждой орбитальной оболочке, принимая во внимание, что 2 электрона помещаются на орбитали.
- Слой s. У него только одна орбиталь, поэтому он может удерживать 2 электрона.
- Слой p. У него 3 орбитали, поэтому есть место для 6 электронов.
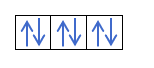
- Слой d. У него 5 орбиталей, поэтому он может удерживать 10 электронов.
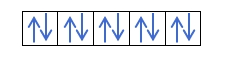
- Слой f. У него 7 орбиталей, то есть он может удерживать 14 электронов.
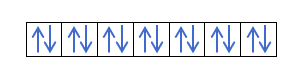
Теперь, когда вы понимаете, что на каждой орбитали есть 2 электрона, вы должны знать правило Хунда. Это правило гласит, что при заполнении орбиталей одного и того же подуровня или оболочки, например, p-оболочки, электроны заполняют орбиталь в одном направлении (положительном), а затем в другом (отрицательном). Хотите увидеть это на примере?
Если у нас есть 2p 4 , то есть 2p-орбиталь с 4 электронами, не будет заполняться следующим образом:
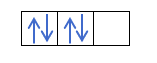
Он будет заливаться так:
Вы это понимаете? Отлично, посмотрим, как считать числа:
- Квантовое число n. Это число совпадает с номером последнего уровня электронной конфигурации. Например, если электронная конфигурация заканчивается через 4 с 2 , главное квантовое число будет 4.
- Квантовое число l. Это число зависит от последнего залитого слоя.
- Слой s -> l = 0
- Слой p -> l = 1
- Слой d -> l = 2
- Слой f -> l = 3
- Квантовое число m. Число m может быть любым значением от -l до + l, поэтому оно будет зависеть от подуровня, на котором находится дифференциальный электрон, то есть от того, является ли он s, p, d или f. Как вычислить это число немного сложнее, давайте посмотрим на это на паре рисунков:
- Слой s -> Как мы видели, l имеет значение 0, поэтому m может иметь значение только 0.
- Слой p -> l стоит 1, поэтому m может быть -1, 0 или 1.
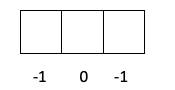
- Слой d -> l равно 2, поэтому m может быть -2, -1, 0, 1 и 2.
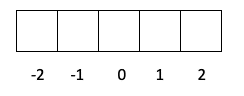
- Слой f -> l стоит 3, поэтому m может быть -3, -2, -1, 0, 1, 2 и 3.
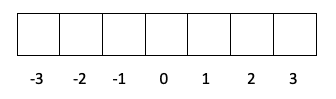
Вы уже знаете, как заполняются орбитали, поэтому квантовое число m будет иметь значение дыры, в которой находится последний нарисованный электрон. Вы помните этот пример раньше ?:
В этом случае m будет -1, так как в p-оболочке (3 орбитали), если есть 4 электрона, последний, который заполнится, будет отрицательным по отношению к первой орбитали.
- Квантовое число s. Квантовое число s может иметь значение только ½ и –½. Если последний нарисованный электрон положительный, то есть стрелка вверх, s будет ½. С другой стороны, если последний электрон, заполнивший орбиталь, отрицателен, то есть со стрелкой, направленной вниз, s будет -½.
Упражнения и примеры
Да, мы уже знаем, что все это много информации, но вы поймете это лучше на некоторых примерах. Вот так!
Пример 1
Селен (Se) -> Атомный номер: 34
- Записываем электронную конфигурацию. Мы записываем электронную конфигурацию согласно диаграмме Меллера, учитывая, что s, p, d и f орбитали имеют 2, 6, 10 и 14 электронов соответственно. Мы записываем конфигурацию, добавляя количество электронов, которое записывается в виде экспоненты.
1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 10 4p 4
Поскольку орбиталь 4p не заполняется, поскольку сумма электронов составит 36, мы не ставим 4p 6 но 4p 4 .
- Вынимаем квантовые числа. Для этого мы смотрим на валентный или дифференциальный электрон, то есть последний электрон, заполнивший орбиталь. В этом случае мы будем смотреть на 4p 4 .
- Главное квантовое число. Последний уровень энергии, который нужно заполнить, был 4.
- Вторичное квантовое число. Последним заполняемым энергетическим подуровнем была p-орбиталь.
- Магнитное квантовое число. Если мы рисуем электроны, последняя заполнится первой орбиталью p-оболочки.
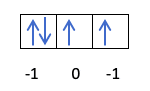
- Спиновое квантовое число. Последний электрон, занявший p-орбиталь, имеет стрелку вниз.
Пример 2
Золото (Au) -> [Xe] 6s 1 4f 14 5d 10
- Главное квантовое число ->N = 5
- Вторичное квантовое число ->l = 2
- Магнитное квантовое число ->м = 2
- Квантовое число спина ->s = -½
И это все! Теперь ваша очередь, не могли бы вы выполнить конфигурацию электронов и получить квантовые числа следующих элементов?:
Cr(24), Rb(37), Br(35), Lu(71), Au(79)
Главная » культура » Квантовые числа
Источник: uniproyecta.com
Квантовые числа электронов.
Квантовые числа – энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.
Квантовые числа – энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.
1. Главное квантовое число n характеризует общую энергию электрона и размер орбитали. Оно принимает целочисленные значения от 1: n = 1, 2, 3, 4, 5, 6, 7.
2. Орбитальное (побочное) квантовое число l характеризует форму атомной орбитали и принимает значения от 0 до n-1: 0, 1, 2, 3, …, n-1.
- Орбитали с квантовым числом l=0 называются s-орбиталями;
- Орбитали с квантовым числом l=1 называются p-орбиталями (3 типа);
- Орбитали с квантовым числом l=2 называются d-орбиталями (5 типов);
- Орбитали с квантовым числом l=3 называются f-орбиталями (7 типов);
Электрон, обладая свойствами частицы и волны, движется вокруг ядра, образуя электронное облако, форма которого в s-, р-, d-, f-, g-состояниях различна.
Если l=0 (s-орбиталь), то электронное облако имеет сферическую форму и не обладает направленностью в пространстве.
Если l=1 (p-орбиталь) то электронное облако имеет форму гантели.
d- и f-орбитали имеют более сложную форму.

3. Магнитное квантовое число m характеризует количество орбиталей одинаковой формы и их ориентацию относительно внешнего электрического или магнитного поля. Квантовое число m принимает целочисленные значения в интервале –l, … –1, 0, +1, … +l. Для каждого значения разрешено 2l+1 значений числа m. Например, если l=1, то m имеет 2×1+1, т.е. 3 значения: –1, 0, +1.
4. Спиновое квантовое число s характеризует вращение электрона вокруг своей оси и принимает только 2 значения: +1/2 (↑) и –1/2 (↓).
Источник: www.calc.ru