Золотое сечение — это особое соотношение сторон фигуры, которое наиболее приятно для созерцания. Это число известно с античных времен, а ученые эпохи Возрождения называли его божественной пропорцией. Число Фи — золотое сечение, приблизительно равное 1,618.
История
Особую красоту деления отрезка на стороны в соотношении 1/1,618 заметили еще античные ученые. Евклид в своих началах использовал этот метод при построении пентагона, а пифогорейцы рассматривали весь мир как царство математической гармонии и уделяли большое внимание соотношению 1/1,618.
В 1202 году Леонардо Фибоначчи вывел особую последовательность, отношение членов которой стремилось к числу Фибоначчи. Лука Пачоли, один из величайших алгебраистов Италии, назвал это соотношение божественной пропорцией, связав свойства бога с числом Фи. Именно с этого момента золотое сечение начало активно использоваться в работах художников эпохи Возрождения и получило буквально мистический статус. По словам Кеплера, число Фи — бесценная жемчужина математики.
О ЗОЛОТОМ СЕЧЕНИИ И ПОЧЕМУ ОНО НАЗЫВАЕТСЯ ЗОЛОТЫМ #золотоесечение
Число Фи в математике
Золотое сечение часто встречается в геометрии. Золотой прямоугольник — фигура на плоскости, длина и ширина которой соотносятся как 1/1,618. Примечательное свойство такого прямоугольника состоит в том, что при удалении из фигуры любого квадрата образуется новый прямоугольник с точно таким же соотношением сторон. Стоит упомянуть и пентаграмму — звездчатый многоугольник, стороны которого пересекаются в соответствии с правилом золотого сечения.
В арифметике число Фи встречается в упоминаемой выше последовательности Фибоначчи, так как lim(Fn/Fn-1) -> Фи. Кроме того, золотое сечение имеет интересное представление в других формах записи. Так, Фи представляется как бесконечная цепочка квадратных корней из единицы. А если привести Фи к цепному виду, то получится бесконечная дробь вида [1; 1, 1, 1, 1, 1…]
Число Фи в реальности
Мистический ореол вокруг золотого сечения возник благодаря такому явлению как «золотой числизм». Энтузиасты, задавшиеся целью найти эту пропорцию в как можно большем количестве реальных объектов или явлений, часто подгоняли результаты. К примеру, храм Парфенон всегда присутствует в списке объектов, которые построены с учетом божественной пропорции. Однако на деле соотношение ширины храма к его высоте составляет 1,74, а если исключить фронтон, то и вовсе 3.
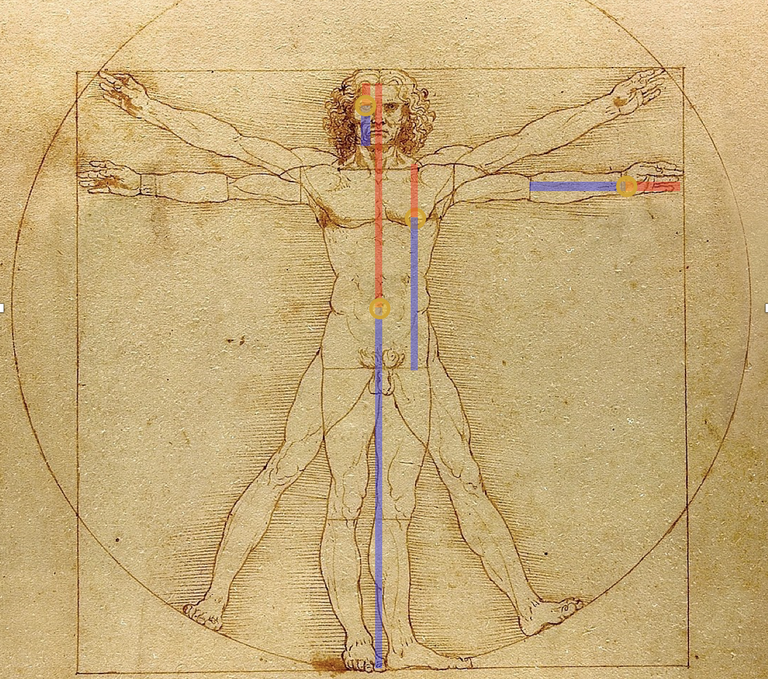
После придания числу божественных свойств, многие художники и музыканты начали сознательно использовать это соотношение в своих работах. Леонардо да Винчи, Альбрехт Дюрер, Иоганн Бах, Ле Корбюзье, Густав Фехнер намеренно придавали своим произведениям форму, соответствующую числу Фи. Одним из современных примеров использования золотого сечения является мозаика Пенроуза — метод непериодического разбиения плоскости.
Несмотря на явное преувеличение свойств золотой пропорции, она все же встречается в реальности. Большинство спиралевидных объектов связны с числом Фи: раковины моллюсков, атмосферные вихри и даже галактики действительно соответствуют божественной пропорции.
Число Фибоначчи = 1.618. Объяснение математического смысла золотого сечения
Калькулятор золотого сечения
Если вы хотите использовать божественную пропорцию в своей работе, то наш калькулятор к вашим услугам. Для определения сторон золотого прямоугольника вам понадобится ввести одну из сторон, а программа определит вторую, соответствующую правилу золотого сечения. Прелесть калькулятора состоит в том, что он не просто умножает сторону на 1,618, а подбирает целое значение. Именно поэтому вам потребуется оперировать целыми числами, что удобно на практике.
Пример из реальной жизни
Живопись
Допустим, вы хотите сделать приятную с точки зрения математики картину, следовательно, вам нужно нарисовать ее на золотом прямоугольнике. Вам потребуется заказать холст определенного размера, и чтобы определить его размеры, используйте наш калькулятор. Пусть вы хотите писать на холсте, длина которого составит 120 см. Как узнать необходимую ширину? Введите это значение в ячейку A и получите ответ, равный 74 см.
Заключение
Божественная пропорция — мистическое соотношение, которое занимает умы математиков уже несколько тысячелетий. Возможно, именно число Фи содержит ответы на вечные вопросы о тайнах мироздания. Если вам потребуется создать объекты, соответствующие золотому сечению, используйте наш калькулятор, при помощи которого вы сможете подобрать целые числа.
Источник: bbf.ru
Золотое и серебряное сечение: в чем различия?
Серебрянное сечение: что это такое, чем отличается от золотого.

Золотое сечение – это определенная закономерность, соотношение чисел, при котором большее число относится к меньшему так же, как сумма этих чисел к большему из них. Его можно встретить во многих арт-объектах, особенно в работах древних архитекторов, скульпторов и художников. Сегодня в художественных школах и академиях наставники сознательно рекомендуют ученикам и студентам использовать в своих работах «золотую пропорцию».
Золотое сечение применяют не только в искусстве, но и в точных науках, например в биологии, физике и математике. Возможно, вы не знали, но помимо широко известного уже упомянутого соотношения существуют и другие, так называемые «металлические» сечения, которые практически не изучены и редко применяются на практике. Можно сказать, что при повсеместном использовании золотого другие металлические соотношения отходят на задний план.
Благодаря стараниям двух сингапурских студентов-математиков постепенно все внимание мира вновь возвращается к «металлическим» константам, которые включают, кроме золотого сечения, все корни квадратного уравнения x² — nx = 1 для положительных значений n. Постепенно увеличивающиеся значения уравнения называются серебряным, бронзовым и другими «металлическими» сечениями.
Золотое сечение гораздо более известно, и мы ассоциируем его с раковиной наутилуса гораздо чаще, чем с фактическим представлением о том, что оно на самом деле воплощает. Согласно перефразированному студентами утверждению древнегреческого математика Евклида, «прямая линия обрезается в соответствии с золотым сечением, когда отношение всей линии к более длинному сегменту равно отношению более длинного сегмента к более короткому».
Другими словами, схема пропорциональных отрезков образует золотое сечение, причем «золотые» отрезки постепенно уменьшаются. В своей статье студенты предлагают ознакомиться с интерактивным графиком, где вы можно проследить зависимость спирали от изменения значений n в режиме онлайн.
Каждая пара смежных целых чисел имеет свою собственную «металлическую пропорцию», которая является собирательным названием для полного набора корней, включающих и золотое сечение. Поясним на примерах: золотое сечение – это средняя пропорция между 1 и 2, серебряное – между 2 и 3, и так вплоть до фермического (химический элемент с порядковым номером 100 в таблице Менделеева) и даже дальше.
Как мы уже говорили, золотое сечение тесно связано с эстетикой и красотой, поэтому активно используется всеми деятелями искусства – от дизайнеров интерьера до кинематографистов. Также не стоит забывать, что «золотая пропорция» переплетается со знаменитой последовательностью Фибоначчи (1, 1, 2, 3, . ), в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее равно сумме двух предыдущих чисел.
Таким образом, соотношение прогрессивных членов последовательности приближается к золотому сечению. Математики из Сингапура утверждают, что и у серебряного сечения есть собственный ряд чисел, называемый последовательностью Пелля. Фактически, можно сказать, что каждая последующая «металлическая пропорция» в свою очередь имеет собственную последовательность с соответствующими математическими закономерностями.



Точно так же, как логарифмическую спираль связывают с золотым сечением, для других металлов тоже существуют свои аналоги. Например, используя «золотое» соотношение, вы рисуете прямоугольник, затем вычеркиваете квадрат со сторонами, равными короткой стороне исходной фигуры. Оставшуюся часть вы поворачиваете на 90 градусов и получаете новый прямоугольник для деления в соответствии с «золотой пропорцией».
И так далее до самой бесконечности. Этот же прямоугольник можно разделить и с помощью других «металлических» соотношений. В каждом из случаев вы вычеркиваете необходимое количество квадратов в соответствии со значениями «металлической пропорции». Например, деля прямоугольник с помощью серебряного сечения, вы вычеркиваете два квадрата и получаете новый, уменьшенный по «серебряной» пропорции прямоугольник.
На данный момент золотое сечение является наиболее известной и широко используемой закономерностью. Однако мы не можем отрицать тот факт, что явления, связанные с «золотой пропорцией», масштабируются и по другим металлическим соотношениям. Нужно лишь немного времени на более тщательное изучение и огласку, и весь мир заговорит и о других «металлах».
Обложка: фото GETTY/KRISHNAVEDALA
Источник: 1gai.ru
Что такое золотое сечение и правда ли оно повсюду
Это соотношение двух неравных чисел, при котором большее так же относится к меньшему, как сумма этих чисел к большему. Золотое сечение равно примерно 1,618, или 1,62, если округлить, и обозначается греческой буквой φ, «фи» — от имени древнегреческого скульптора Фидия. Считается, что он использовал такие пропорции при оформлении Парфенона.
Наиболее известные графические представления золотого сечения — это прямоугольник с соотношением сторон примерно 62:48 и построенная в нём спираль.
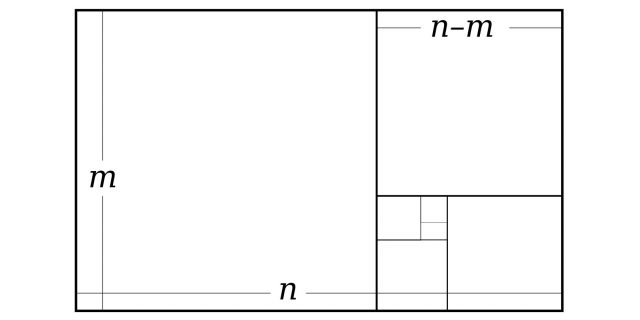
«Золотой прямоугольник» можно разделить на такие же, только меньшего размера. Изображение: Dicklyon / Wikimedia Commons
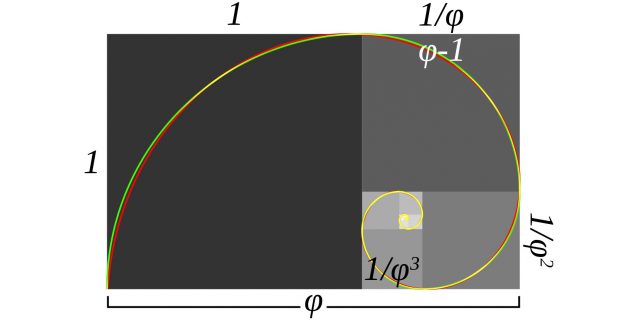
«Золотая спираль» (красная), вписанная в «золотой прямоугольник». Изображение: Silverhammermba 8/5=1,6, а 34/21= 1,619.
Почему золотое сечение так популярно
Впервые им заинтересовались ещё древнегреческие математики Пифагор и Евклид. Они считали, что на числах построено всё мироздание и с их помощью можно объяснить любой феномен. Неудивительно, что элегантное соотношение так заинтересовало античных мыслителей.
Вслед за ними золотым сечением увлеклись многие выдающиеся учёные и деятели искусства. Например, Леонардо да Винчи, Альбрехт Дюрер, Иоганн Кеплер, Ле Корбюзье, Сальвадор Дали и Ричард Пенроуз.
Его считают «божественной пропорцией»
Название «золотое сечение» придумал немецкий математик XIX века Мартин Ом. До него это соотношение именовали «божественной пропорцией».
Из‑за приписываемых характеристик золотое сечение старались применять как можно чаще. Так, во времена Возрождения это число считалось идеальным способом для выбора размера. «Золотой прямоугольник», например, нередко использовали при создании книг и картин. А линию пояса называли границей золотого сечения человеческого тела.
Некоторые и поныне считают эту пропорцию секретом привлекательности и примером универсальной гармонии, приятной человеческому глазу. Например, о золотом сечении любят говорить пластические хирурги. А ещё это число популярно как никакое другое в математике.
Его можно встретить в природе
Числа Фибоначчи и спирали, подобные золотому сечению, часто обнаруживаются в природе. Например, в количестве лепестков у цветов или форме растений.

Знание о числе φ играет важную роль в изучении хаоса и изменяющихся (динамических) систем. Оно помогает понять, как природа развивается и самоорганизуется.
Также числа Фибоначчи полезны при решении некоторых сложных задач. Например, с помощью этих чисел советский математик Юрий Матиясевич доказал , что не существует универсального алгоритма решения уравнений с как минимум двумя неизвестными.
- Продолжите последовательность! 10 мини-задач для разминки мозга
- Как округлять числа
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- Гимнастика для ума: 10 увлекательных задач с числами
- 10 увлекательных задач от советского математика
Источник: lifehacker.ru