Длина свободного пробега электрона в золоте

Частицы газа находятся в состоянии теплового движения, постоянно взаимодействуя (сталкиваясь) друг с другом. Число столкновений z, испытываемых какой либо частицей на пути в 1 см, пропорционально концентрации N. Величина, обратная числу столкновений, l=1/z представляет собой среднюю длину свободного пробега частицы. Действительные длины свободных пробегов подвержены значительному разбросу. Вероятность того, что длина свободного пробега частицы равна или больше x, cоставляет

Если больше энергии ионизации , то при столкновении электрона с нейтральной частицей может произойти ионизация. Если энергии электрона недостаточно для этого, то возможно возбуждение частицы, а при столкновении с возбужденной частицей, находящейся в метастабильном состоянии, такой электрон может участвовать в процессе ступенчатой ионизации.Расстояние, который должен пролететь электрон, чтобы накопить достаточную для ионизации энергию, определяется как

и зависит от напряженности электрического поля.Вероятность того, что электрон пролетит путь без столкновений, составляет

Физическая кинетика. Часть 1. Длина свободного пробега. Эффективный диаметр.

но это и есть вероятность приобретения электроном энергии , при которой возможна ионизация, т.е. можно считать вероятностью ионизации.

Дата добавления: 2016-06-22 ; просмотров: 2624 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник: poznayka.org

Большая Энциклопедия Нефти и Газа

Считалось, что длина свободного пробега в стеклах и жидкостях не превышает одного-двух межмолекулярных расстояний, хотя хорошо известно, что в жидких металлах длина пробега электронов того же порядка, что и в твердых. Сравнивая ход электропроводности до и после плавления в полупроводниках, где плавление не изменяет ближнего порядка, можно прийти к заключению, что не только ширина запрещенной зоны, но и подвижность мало изменяются после плавления. Если структурные флюктуации имеют в жидкостях атомные размеры, а длина электронных волн в десятки раз больше их, то возможно, что вероятность рассеяния свободных зарядов на таких неоднородностях невелика, а малая вязкость быстро выравнивает всякие другие дефекты с большим поперечным сечением рассеяния. [31]

Численные значения коэффициентов ослабления для р-излу-чения сравнительно велики ( для р-лучей они на два или три порядка больше, чем для — у-лучей), что приводит к уменьшению длины пробегов электронов в конденсированных средах до нескольких миллиметров. Это часто упрощает решение общей дозиметрической проблемы, позволяя при расчете учитывать только одно ослабление. Если, например, тело больших размеров облучается пучком электронов, так что расстояние между источником излучения и поверхностью объекта облучения велико по сравнению с длиной пробега электронов в веществе ( например, 10 см и 5 мм соответственно), то можно при расчете дозы пренебречь изменением расстояния с увеличением глубины или же потом внести в результат соответствующие малые поправки. [32]

Длина свободного пробега

Получили распространение фотокатоды с отрицательным электронным сродством — полупроводники с большой дырочной проводимостью, у которых под влиянием активных адсорбированных пленок ( обычно цезия или комбинации цезия с кислородом) происходит в пределах приповерхностного слоя ( порядка длины пробега электрона ) такой изгиб энергетических зон, что уровень вакуума оказывается ниже зоны проводимости в глубине кристалла. По отношению к глубинным электронам электронное сродство становится отрицательным. Поэтому электронам, возбужденным светом в зону проводимости, для выхода в вакуум не нужна дополнительная энергия. [33]

В действительности длина свободного пробега электронов по отношению к рассеянию их друг другом может быть значительно больше этого значения. Оценив длины пробега электрона по отношению к различным процессам, можем выяснить, как зависит электропроводность или сопротивление металла от температуры и концентрации примесей. [34]

Характерной особенностью большой группы электронных приборов является наличие в них сфокусированного пучка — электронного луча. В электронных лампах длина пробега электронов между электродами измеряется в большинстве случаев в миллиметрах, а электронный луч имеет длину 10 — 20 см. и более. В электронных лампах осуществляется управление интенсивностью потока электрона между электродами, а в электроннолучевых приборах кроме управления интенсивностью электронного луча осуществляется также управление направлением этого луча. [36]

Электроны при прохождении через вещество испытывают неупругое и упругое рассеяния; последнее описывается формулой Резерфорда ( стр. Ионизация на единицу длины пробега электрона в первом приближении пропорциональна р NAZ / Av %, где р — плотность, А — атомный вес, NA — число Авогадро, Z — атомный номер вещества, о — начальная скорость электрона. [37]

Такие потери называются радиационными. Ионизационные и радиационные потери определяют длину пробега электрона в веществе. [38]

Таким образом, промышленное применение электронного излучения ограничивается облучением тонкостенных изделий, листовых, профильных материалов. Толщина этих изделий должна быть меньше длины пробега электронов в применяемых материалах. При энергии электронов 2 МэВ равномерная радиационная обработка полиэтилена может быть проведена на глубину около 10 мм. [39]

При прохождении через базу горячие электроны теряют энергию из-за столкновений с другими электронами и атомами. Если толщина металла меньше LM — длины поглощения ( длина пробега электронов в металле, на которой их скорость уменьшается в е раз), то значительная часть электронов доходит до коллекторного барьера Шоттки с малыми потерями энергии и может пройти через него. [41]

Отметим, что импеданс (86.23) оказывается не зависящим вовсе от длины пробега электронов . [42]

Отметим, что импеданс ( 86 23) оказывается не зависящим вовсе от длины пробега электронов . [43]

Согласно этой теории движение электронного газа подчиняется классическим законам перемещения газообразных молекул. С ростом температуры диапазон тепловых колебаний катионов возрастает, за счет чего увеличивается длина пробега электронов в кристалле и, как следствие, снижается его электропроводность. [44]

Согласно этой те ории, движение электронного газа подчиняется классическим законам перемещения газообразных молекул. С ростом температуры диапазон тепловых колебаний катионов возрастает, за счет чего увеличивается длина пробега электронов в кристалле и, как следствие, снижается его электрическая проводимость. [45]

Источник: www.ngpedia.ru

2.1. Общие сведения

При наличии градиента потенциала в проводящих средах происходит направленный перенос электрического заряда – течет электрический ток. Кинетическая энергия, приобретаемая электронами при действии на них электрического поля, вследствие рассеяния электронов на нерегулярностях кристаллической решетки превращается в джоулево тепло, т. е. перенос электрического заряда в проводнике характеризуется некоторым электрическим сопротивлением. Удельная электропроводность металла определяется формулой Друде-Лоренца

, (2.1)

где n – концентрация электронов проводимости («свободных» электронов), e – заряд электрона, – его эффективная масса, а – средняя длина свободного пробега электронов, обладающих энергией Ферми , т. е. движущихся с фермиевской скоростью

. (2.2)

Для образца с достаточно большими геометрическими размерами длина свободного пробега ограничивается рассеянием свободных электронов на внутренних нерегулярностях кристаллической решетки: тепловых колебаниях (фононах), примесных атомах и других дефектах структуры. В этом случае значение определяется только свойствами самого металла и не зависит от геометрии образца, т. е. значение удельной электропроводности является характеристикой материала, а не образца.

По мере сокращения поперечных размеров проводника (тонкие пленки, проволоки малого диаметра), заметную роль начинает играть ограничение длины свободного пробега электронов поверхностями образца, которые действуют как дополнительные рассеивающие центры. Вследствие этого длина свободного пробега электронов, а, следовательно, и удельная электропроводность утрачивают свойства констант данного вещества и становятся зависящими от конкретных геометрических размеров образца – возникает размерный эффект в электропроводности. Впервые на размерный эффект в образцах с малым поперечным сечением указал Дж. Дж. Томсон в 1901 г.

Рассмотрим размерный эффект в пленке, т. е. в образце, ограниченном двумя параллельными плоскостями. В принципе, теория данного явления должна строиться на основе уравнения Больцмана, описывающего кинетику электронного газа во внешнем электрическом поле при учете рассеяния электронов на границах образца. Однако даже в простейших случаях решение этого уравнения сопряжено с большими трудностями. Поэтому мы ограничимся здесь элементарным физическим анализом размерного эффекта, который позволит нам получить оценочные формулы, справедливые по порядку величины, а затем приведем без вывода результаты последовательной кинетической теории.

Итак, обратимся сначала к случаю толстой пленки, т. е. пленки, толщина h которой много больше средней длины свободного пробега

электрона в рассматриваемом металле. Длина волны, отвечающая блоховской волновой функции электрона с энергией , составляет доли нанометра.

Характерные же размеры шероховатостей, всегда имеющихся на поверхности пленки, редко оказываются меньше 10-100 нм. Поэтому рассеяние электрона на границе образца неизбежно сопровождается изменением касательной составляющей его импульса (скорости); такое рассеяние называется диффузным. Диффузное рассеяние порождает дополнительное электросопротивление, которое можно оценить следующим образом. Будем считать, что электроны, рассеивающиеся на границах образца, тормозятся настолько сильно, что вообще не участвуют в переносе заряда. Доля таких электронов, находящихся в пристеночных слоях с толщиной порядка , составляет, очевидно, величину порядка . Соответственно, эффективная проводимость материала с учетом размерного эффекта должна отличаться от объемной на фактор :

. (2.3)

Последовательный расчет на основе кинетического уравнения Больцмана в случае толстых пленок дает:

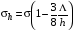
. (2.4)

Как и следовало ожидать, наша грубая оценка вклада поверхностного рассеяния в электросопротивление пленки оказалась завышенной. Реально, конечно, средняя скорость электронов в пристеночных слоях отлична от нуля, и они участвуют (хотя и в меньшей мере, чем электроны в объеме) в формировании полного тока.

Рассмотрим теперь случай тонких пленок, для которых . В этом пределе рассеяние электронов на границах образца доминирует над другими видами рассеяния (электрон-фононным, дефектным), и эффективная длина свободного пробега

должна по порядку величины совпадать с толщиной пленки h. Это значит, что средняя длина пробега электрона в пленке уменьшается по сравнению с массивным образцом примерно в раз. Во столько же раз должна падать и эффективная электропроводность:

. (2.5)

Рис.1. Зависимость

1 – теория, 2 – эксперимент

Реально, однако, ситуация оказывается несколько сложнее. Дело в том, что оценка справедлива не для всех электронов, а лишь для тех, чьи импульсы почти перпендикулярны поверхности пленки. Но эти электроны практически не дают вклада в ток.

Электроны же, движущиеся под углом к нормали и участвующие в формировании тока, имеют длины пробега, существенно превышающие h. В результате средняя эффективная длина свободного пробега электрона в тонкой пленке оказывается заметно большей, чем h, и

вследствие размерного эффекта падает не столь сильно, как предписывает формула (2.5). Решение задачи в рамках уравнения Больцмана подтверждает этот вывод. В пределе оно дает:

. (2.6)

Формулы (2.4) и (2.6) справедливы, как указывалось, в асимптотических областях 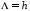и . При промежуточных толщинах простое аналитическое выражение для получить не удается.

Графическая зависимость от h представлена на рис. 2.1 (кривая 1). Здесь же приведена и типичная зависимость , полученная в эксперименте (кривая 2). Значения и реальных пленок обычно оказываются меньше рассчитанных. Это расхождение обусловлено особенностями структуры реальных пленок (наличием зерен, островков, инородных включений), которые в свою очередь тесно связаны с технологией их изготовления.

Как следует из выражений (2.4), (2.6) и графика на рис. 2.1, заметные изменения эффективной электропроводности наблюдаются при толщине пленки, по порядку величины равной или меньшей длины свободного пробега электронов в массивном образце. Так как для большинства чистых металлов при комнатной температуре = 30…50 нм, а обычно используемые проводники имеют поперечные размеры более 1 мкм, то в них размерный эффект не проявляется. В этих случаях можно пользоваться значениями , полученными на массивных образцах. В то же время тонкопленочные элементы современных микроэлектронных устройств могут иметь толщины, при которых размерный эффект становится ощутимым.

Аналогичные размерные эффекты имеют место и для других параметров вещества, например, для температурного коэффициента сопротивления, коэффициента теплопроводности, термоЭДС и т. п.

Источник: studfile.net