Задание 20. Из ядер платины при -распаде с периодом полураспада 20 часов образуются стабильные ядра золота. В момент начала наблюдения в образце содержится ядер платины. Через какую из точек, кроме начала координат, пройдёт график зависимости числа ядер золота от времени (см. рисунок)?

Число не распавшихся ядер N можно определить по формуле
где T=20 часов – период полураспада; — начальное число ядер. На рисунке показано число образовавшихся ядер золота, поэтому скорректируем эту формулу так:
Для точки 1, имеем t=20 ч и
Для точки 2 t=40 ч и
Подходит. Следовательно, график пройдет через точку 2.
Источник: self-edu.ru
Изотоп платины в результате одного бета распада переходит в радиоактивный изотоп золота
Тысячи правильных ответов на различные тесты
Химическая эволюция вселенной | Дмитрий Вибе
Тысячи проверенных ответов
Вопрос теста:
Платина  в результате одного β–распада переходит в радиоактивный изотоп золота
в результате одного β–распада переходит в радиоактивный изотоп золота  , который затем превращается в стабильный изотоп ртути
, который затем превращается в стабильный изотоп ртути  .
. 
На рисунке приведены графики изменения числа атомов с течением времени. Какой график может относиться к изотопу  ?
?
- 2
- 3
- 1
- ни один из графиков
Урок 2. «Решение задач по теме «Закон радиоактивного распада. Период полураспада»
На этом уроке учащимся предлагается поработать в парах. Используется эффект взаимообучения.
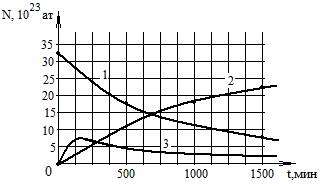
1. На рисунке приведена зависимость числа не распавшихся ядер N от времени в процессе радиоактивного распада для трех изотопов. Для какого из них период полураспада минимален?
1) I 2) II 3) III 4) у всех одинаков

Ответ: _____
2. Ядра платины испытывают распад с периодом полураспада 20 часов. В момент начала наблюдения в образце содержится ядер платины. Через какую из точек, кроме точки А, пройдет график зависимости от времени числа еще не испытавших радиоактивный распад ядер платины? Период полураспада данного изотопа платины равен 20 суткам.

Ответ: _____
3. Платина в результате одного распада переходит в радиоактивный изотоп золота , который затем превращается в стабильный изотоп ртути . На рисунке приведены графики изменения числа атомов всех трех изотопов с течением времени. Какой график относится к изотопу ? ? ?
Закон радиоактивного распада. Период полураспада
4. Из 20 одинаковых радиоактивных ядер за 1 мин испытало радиоактивный распад 10 ядер. За следующую минуту испытают распад
1) 10 ядер 2) 5 ядер3) от 0 до 5 ядер 4) от 0 до 10 ядер
5. Радиоактивный препарат содержит 40 млрд одинаковых радиоактивных ядер некоторого химического элемента. Если за одну минуту испытали распад 20 млрд ядер, то число ядер, которые распадутся за следующие две минуты, равно
1) 10 млрд 2) 15 млрд 3) 20 млрд 4) 25 млрд
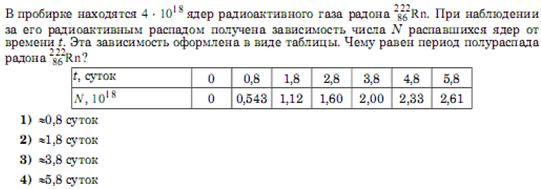

8. Период полураспада радона 3,8 дня. Через какое время активность радона уменьшится в 64 раза?
9. Чему равен период полураспада изотопа, если за двои сутки распалось в среднем 984375 атомов из 1000000?
10. Упр. 14 (3) учебник. Во сколько раз уменьшится число атомов одного из изотопов радона за 1,91 сут.? Период полураспада этого изотопа радона Т = 3,82 сут.
11. Сколько по массе радиоактивного вещества останется по истечение 3 суток, если вначале его было 100 г? Период полураспада вещества равен двум суткам.
12. Период полураспада первого элемента в 2 раза меньше периода полураспада второго элемента. За некоторое время число атомов первого элемента уменьшилось в 16 раз. Во сколько раз за это же время уменьшилось число атомов второго элемента?
1) в 2 раза 2) в 4 раза 3) в 8 раз 4) в 256 раз
13. Чему равен период полураспада атомов радиоактивного элемента, если за сутки интенсивность излучения образца этого элемента падает на 5%?
14. Пациенту ввели внутривенно V 0 = 1 см 3 раствора, содержащего изотоп общей активностью а 0 = 2000 распадов в секунду. Период полураспада изотопа равен T = 15,3 ч. Какова активность такой же по объёму пробы крови пациента через t = 3 ч 50 мин, если общий объём крови пациента V = 6 л? Переходом ядер изотопа из крови в другие ткани организма пренебречь.
Задания 1-3 – графические. Особенно интересно третье, в котором показано, что часто происходит цепочка радиоактивных превращений. И если количество исходных радиоактивных ядер только убывает, а конечных стабильных – только возрастает, то количество промежуточных ядер меняется сложнее: сначала их не было, затем их количество растёт, а потом заметно начинает проявляться результат их распада.
Задание 4 на статистический характер закона радиоактивного распада. Для 10 ядер закон не выполняется. Этого большинство учащихся не замечают.
В задании 6 информация представлена в табличной форме. В таблице дано количество распавшихся ядер.
Задание 7 позволяет напомнить учащимся о методе спектрального анализа. Также в нём полезно записать уравнение бета-распада углерода, чтобы убедиться, что в результате появляется азот.
Задание 8 можно решать устно. Речь об активности.
Задание 9 – расчётное. В условии дано количество распавшихся ядер.
В 10 и 11 заданиях необходимо работать по формуле, т.к. время не равно целому числу периодов полураспада. Учащимся снова напоминается о нелинейности зависимости количества не распавшихся ядер от времени.
Задание 12 требует внимания.
Задание 13 полезно применить логарифмирование.
Задание 14 – задача 32 (раньше С6) из реального ЕГЭ. Прямая.

2. Из ядер платины при β – -распаде с периодом полураспада 20 часов образуются стабильные ядра золота. В момент начала наблюдения в образце содержится 8⋅10 20 ядер платины. Через какую из точек, кроме начала координат, пройдёт график зависимости числа ядер золота от времени (см. рисунок)?
3. Период полураспада первого элемента в 2 раза больше периода полураспада второго элемента. За некоторое время число атомов первого элемента уменьшилось в 32 раза. Во сколько раз за это же время уменьшилось число атомов второго элемента?
1) в 5,7 раза 2) в 16 раз 3) в 256 раз 4) в 1024 раза
4. Образец радиоактивного радия находится в закрытом сосуде, из которого откачан воздух. Ядра радия испытывают α-распад с периодом полураспада 3,6 суток. Определите число моль гелия в сосуде через 10,8 суток, если образец в момент его помещения в сосуд имел в своём составе 6⋅10 23 атомов , а атомов гелия в сосуде не было.
5. Пациенту ввели внутривенно дозу раствора, содержащего изотоп . Активность 1 см 3 этого раствора а 0 = 2000 распадов в секунду. Период полураспада изотопа равен T = 15,3 ч. Через t = 3 ч 50 мин активность 1 см 3 крови пациента стала а = 0,28 распадов в секунду. Каков объём введённого раствора, если общий объём крови пациента V = 6 л? Переходом ядер изотопа из крови в другие ткани организма пренебречь.
Если в классной работе последняя задача типа С6 ЕГЭ была прямая, то на дом для закрепления даётся обратная задача.
Открытый банк заданий ЕГЭ ФИПИ
Тренировочные работы МИОО
Физика: типовые экзаменационные варианты / под ред. М.Ю. Демидовой (разных лет)
Другие книги для подготовки к ЕГЭ по физике
Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г.Я.Мякишев, Б.Б.Буховцев, В.М. Чаругин. — М.: Просвещение, 2010
Физика Задачник. 10-11 кл.: пособие для общеобразоват. учреждений / А.П. Рымкевич. – 12-е изд., стереотип. – М.: Дрофа, 2008
Источник: poisk-ru.ru