Сумма масс меди в двух первых сплавах равна массе меди в полученном сплаве:

Решив это уравнение, получаем х=140. При этом значении х выражение
200 – х=60. Это означает, что первого сплава надо взять 140г, а второго 60г
Ответ: 140 г, 60г.
Задача №2 Имеется два сплава золота и серебра. В одном количество этих металлов находится в отношении 1:9, а в другом 2:3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золота и серебро относилось бы как 1:4?
Теперь внесем данные в таблицу:
Сумма масс золото в двух первых сплавах равна массе золота в новом сплаве
Ответ: 10 кг и 5 кг.
Решение задач с помощью математической модели
Графические иллюстрации к условию задач помогают найти правильный путь к ответу на вопрос задачи.
Изобразим каждый из растворов в виде прямоугольника, разбитого на два фрагмента (по числу составляющих элементов). Для того, чтобы показать, что происходит смешивание веществ поставим знак «+» между первым и вторым прямоугольниками, а знак «=» между вторым и третьим прямоугольниками показывает, что третий раствор получен в результате смешивания первых двух. Полученная схема имеет следующий вид:
ДВИ по математике в МГУ, 2023 год, 3 поток, задача 7 (стереометрия)
Решим задачу №1 данным способом.
Задача №1 Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Рассматриваемый в задаче процесс можно представить в виде следующей модели-схемы:

Пусть х г – масса первого сплава. Тогда, (200- х)г – масса второго сплава. Дополним последнюю схему этими выражениями. Получим следующую схему:

Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):

Решив это уравнение, получаем х=140. При этом значении х выражение 200- х=60. Это означает, что первого сплава надо взять140г, а второго-60г.
Задача №3 Сколько граммов воды нужно добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить сироп, концентрация которого равна 20%?
Источник: poisk-ru.ru
Различные способы решения задач на смеси, сплавы , растворы
![]()

- Рассматривая учебники по математике разных авторов, я увидела несколько совершенно разных по типу задач на растворы, а решения одних и тех же задач в одних учебниках были совершенно другими, нежели в других. Поэтому выдвинула свою гипотезу:
- Гипотеза: все задачи на растворы, сплавы и смеси делятся на несколько типов, а каждый из типов имеет конкретный способ решения.
Как решать задачи на сплавы и смеси

- Систематизировать задачи на растворы, смеси и сплавы;
- Найти единый алгоритм решения этих задач;
- Научиться решать задачи по заданной теме.
ЕГЭ и межпредметная связь

- Созданный мною проект содержит материал по теме «Проценты» из курса математики, который может помочь также и при решении заданий на проценты не только в тестах ЕГЭ по математике за курс основной и средней школы, а так же при изучении химии, биологии, физики и других предметов.
- В ходе проектной деятельности я проводила опрос «Можете ли вы решать задачи на растворы?». Вот результаты первого:

Для решения задач на концентрации нужно уметь рассуждать и решать задачи на дроби и проценты, на составление уравнений и их систем. Эти задачи решаются арифметически, применением линейного уравнения и их систем, и другие способы.
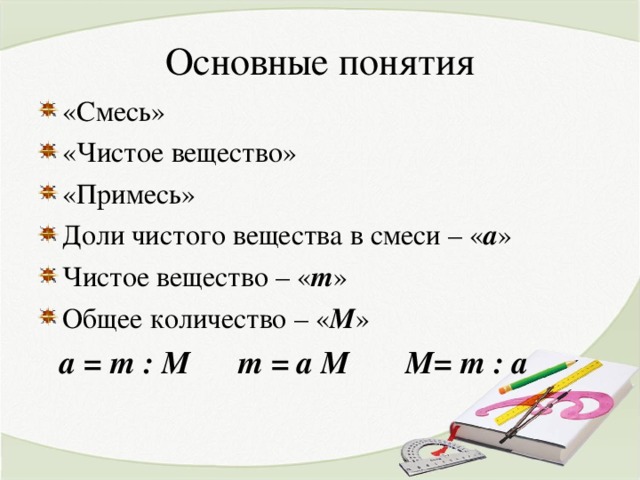
- «Смесь»
- «Чистое вещество»
- «Примесь»
- Доли чистого вещества в смеси – « a »
- Чистое вещество – « m »
- Общее количество – « М »
a = m : M m = a M M = m : a
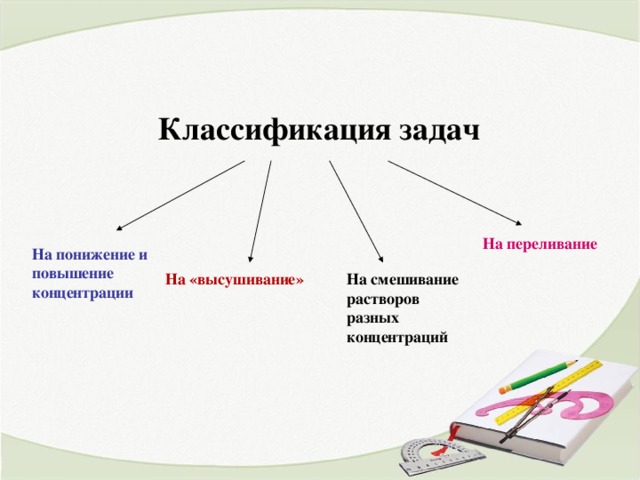
Классификация задач
На переливание
На понижение и повышение концентрации
На «высушивание»
На смешивание растворов разных концентраций
Задачи на понижение и повышение концентрации
Задача №2: сплав массой 36 кг содержит 45% меди. Сколько меди нужно добавить, чтобы новый сплав содержал 60% меди?

Решение задачи №1
II . Правило «креста»
I . Пусть надо добавить х кг воды. Заполним таблицу по условию задачи.
Значит, 40 кг – 15 частей тогда, чтобы получить 15% р-р нужно добавить 3 части воды
Составим и решим уравнение:
Источник: kopilkaurokov.ru
Математика задачи на сплавы золото и серебро

Имеется 600г сплава золота с серебром, содержащего золото и серебро в отношении один к пяти соответственно. Сколько граммов серебра надо добавить к этому сплаву, чтобы новый сплав содержал 80% серебра?
Комментарии

Антиспамеры! Неправильное условие задачи. Изначально серебра БОЛЬШЕ 80%, а по условию «серебра надо добавить к этому сплаву, чтобы новый сплав содержал 80% серебра».
Эта задача из сборника Трениовочная работа для 9 класса по теме «Решение задач на смеси и сплавы» http://prntscr.com/5nl0qq В задаче ошибка Решение верное . Просьба не отмечать задачц как неверную

Ответ проверен экспертом
4 (3 оценки)

hot0808 8 лет назад
Светило науки — 644 ответа — 0 раз оказано помощи
1) 1+5=6 частей золота и серебра в первом сплаве
2) 600/6=100 гр вес каждой из частей
3) 5*100=500 грамм серебра в первом сплаве.
4) 500/600*100=83,33% серебра содержит этот сплав
Следовательно для получения сплава, содержащего 80% серебра, его нужно отнять. Пусть отнимем х граммов серебра и получим сплав, содержащий 80% серебра, тогда
(600-х)*0,8=500-х
480-0,8х=500-х
х-0,8х=500-480
0,2х=20
х=20/0,2
х=100 грамм
Проверка: отнимем 100 грамм серебра.
1) 600-100=500 грамм — общий вес сплава
2) 500-100=400 грамм серебра в сплаве
3) 400/500*100=80% серебра содержит новый сплав
Источник: vashurok.com