Рассчитаем коэффициент диффузии частиц гидрозоля золота:
= 7,154 10 − 11 м 2 .
6 3,14 1 10 − 3 Па с 3 10 − 9
Рассчитаем удельную поверхность s уд
(в м -1 ) по уравнению (1.3):
Рассчитаем удельную поверхность
s ′ уд частиц гидрозоля золота (в
Пример 3.3. Найдите радиус частиц гидрозоля золота, если после установления седиментационно-диффузионного равновесия при 293 К на высоте 15 см концентрация частиц изменяется в е раз. Плотность частиц гидрозоля примите равной 19,3 г/см 3 , плотность дисперсионной среды 1,0 г/см 3 .
Распределение частиц по высоте при установлении седиментацион- но-диффузионного равновесия описывается гипсометрическим законом (3.11). Для сферических частиц имеем:
Согласно условию задачи
= 1. Далее используем
гипсометрический закон для расчета радиуса частиц:
= 3,3 10 − 9 м = 3,3 нм
Пример 3.4. Постройте кривую седиментации и, используя метод касательных, рассчитайте и постройте интегральную и дифференциальную кривые распределения частиц суспензии по размерам. Для расчёта необходимы данные о плотности ρ 0 и вязкости η дисперсионной среды, плотности
3 6 Осмос Коллигативные свойства растворов
частиц ρ, высоте оседания h и данные о кинетике седиментации – зависимость массы осевших частиц от времени m=f( τ ) (кривая седиментации) .
Строим кривую седиментации m = f (τ); её типичный вид представлен на рис. 3.1.
Максимальную массу осевших частиц обозначим m max (рис. 3.1). Время, за которое достигается m max , обозначим τ max . Разделим весь временной интервал от τ =0 до τ = τ max на 10-20 участков (τ i ).
Рис. 3.1. Кривая седиментации для полидисперсной системы
Для каждого времени τ i по уравнению (3.9) рассчитываем диаметр частиц d i , которые за это время полностью осели из суспензии при высоте ее столба, равной h :
Источник: studfile.net
Определить осмотическое давление гидрозоля золота концентрацией 2 кг/м3 с диаметром частиц 6*10-9 м и плотностью 19,3*103 кг/м3 при 293К

Готовое решение: Заказ №8423

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

140 грамм ЗОЛОТО 999 Как правильно пользоваться гидроксиламином солянокислым
Предмет: Химия

Дата выполнения: 05.09.2020

Цена: 228 руб.
Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
Определить осмотическое давление гидрозоля золота концентрацией 2 кг/м 3 с диаметром частиц 6*10 -9 м и плотностью 19,3*10 3 кг/м 3 при 293К
Решение:
2 кг золота занимают объем

Объем отдельной коллоидной частицы вычисляем по формуле объема шара:

- Объем газообразного азота Vm при 1,04*105 Па и 273К, необходимый для покрытия образца силикагеля мономолекулярным слоем 129 мл/г. Вычислить площадь
- Коллоидный раствор получен в результате реакции обмена при смешивании равных объемов растворов А и В равных концентраций. Напишите и объясните формулу
- Для обратимой реакции первого порядка Кравн=8, ak1=0,4 с-1. Вычислите время, при котором концентрации веществ А и В станут равными, если начальная концентрация
- Найдите средний сдвиг частиц дыма хлористого аммония с радиусом 10-6 м при 273К за время 6 сек. Вязкость воздуха η = 1,7*10-5 Н*с/м2. Как изменится сдвиг
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
В случае копирования материалов, указание web-ссылки на сайт natalibrilenova.ru обязательно.
Источник: natalibrilenova.ru
Гаврилова Н.Н., Жилина О.В. Сборник задач по коллоидной химии
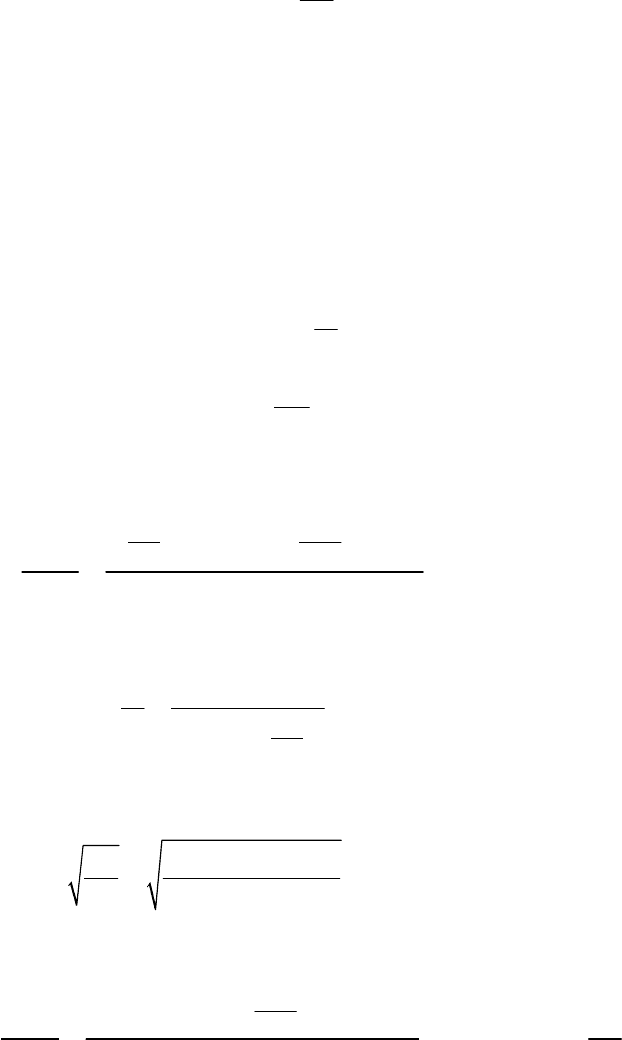
мость массы осевших частиц от времени m=f( τ ) ( кривая седиментации ) .
Алгоритм решения :
Строим кривую седиментаци и m = f ( τ ); её типичный вид представлен
на рис . 3.1.
Максимальную массу осевших частиц обозначим m
Время , за которое достигает ся m
, обозначим τ
Разделим весь времен —
ной интервал от τ =0 до τ = τ
на 10-20 участков ( τ
Рис . 3.1. Кривая седиментации для полидисперсной системы
Для каждого времени τ
по уравнению (3.9) рассчитываем диаметр
, которые за это время полностью осели из суспензии при высоте
ее столба , равной h :
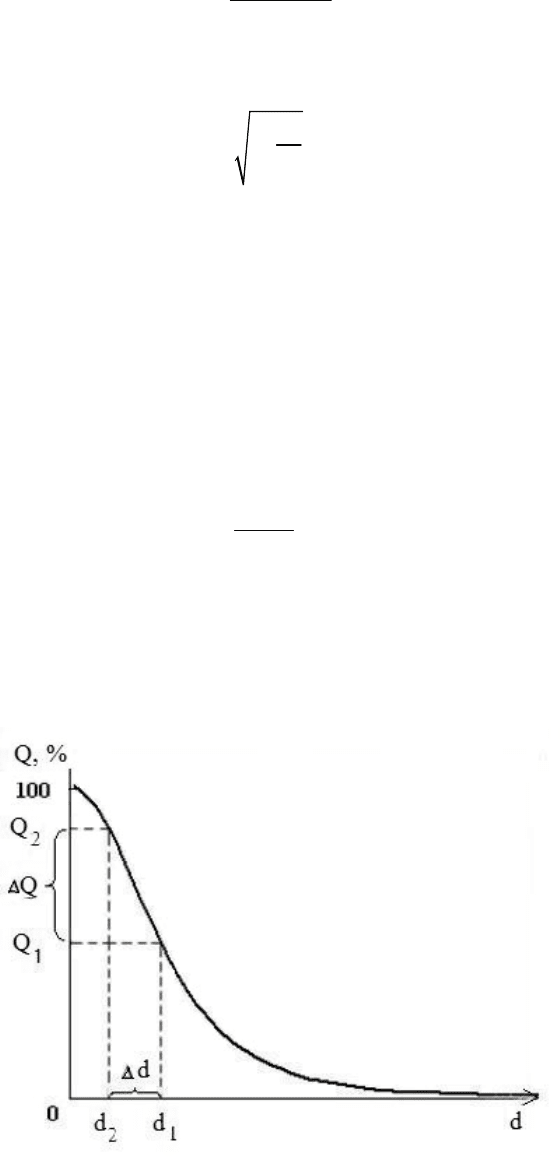
Для упрощения расчётов все постоянные величины удобнее объеди —
нить и обозначить как некую константу К :
С учётом этого уравнение (3.4) принимает вид :
В выбранных точках кривой седиментации , соответствующих τ
проведём касательные и определим з начения m
, которые соответствуют
отрезкам , отсекаемым на оси ординат этими касат ельными ( рис . 3.1). Ве —
– это масса частиц , диаметры которых равны и больше d
рассчитываем значение Q
– процентное фракции
частиц с диаметрами , равными и большими d
Полученные знач ения Q
использу ем для построения интеграль —
ной кривой распределения частиц по размерам Q = f(d). Её типичный вид
представлен на рис . 3.2.
Рис . 3.2. Интегральная кривая распределения частиц по размерам
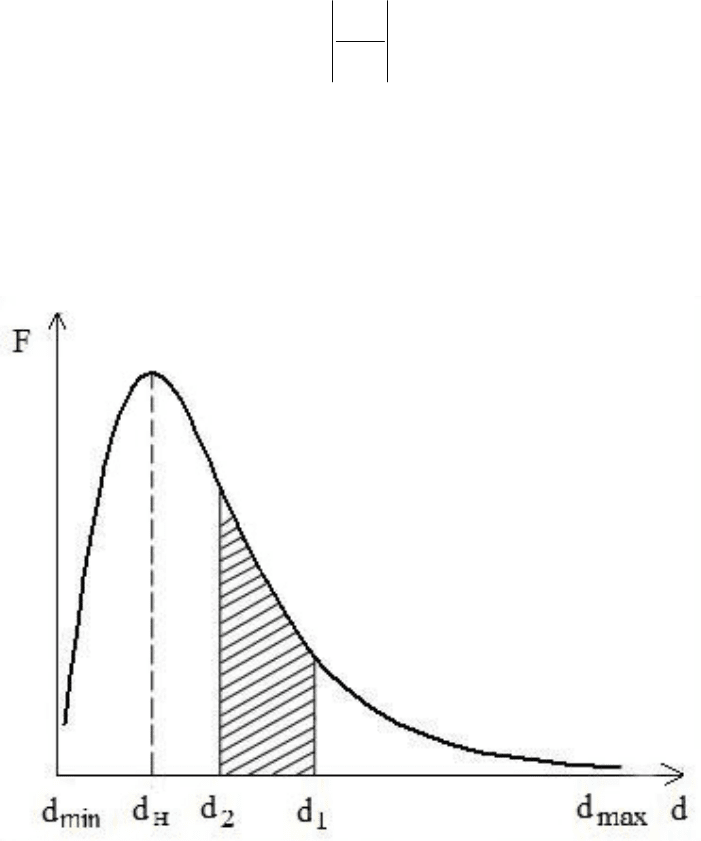
Интегральная кривая позволяет определить процентное
частиц в различных фракциях : например , для фракции , содержащей части —
цы размерами от d
Для построения дифференциальной кривой распределени я частиц по
размерам F = f(d) необходимо продифференцировать зависимость Q = f(d) .
Для этого делим интервал от d
на 10-20 участков . Определив для
каждого участка соответствующее приращение Δ Q
, рассчитываем значе —
При построении зависимост и
F = f(d) значения F
относят к среднему
для каждого интервала диаметру . Типичный вид дифференциальной кри —
вой распределения частиц по размерам приведен на рис . 3.3.
Рис . 3.3. Дифференциальная кривая распределения частиц по размерам
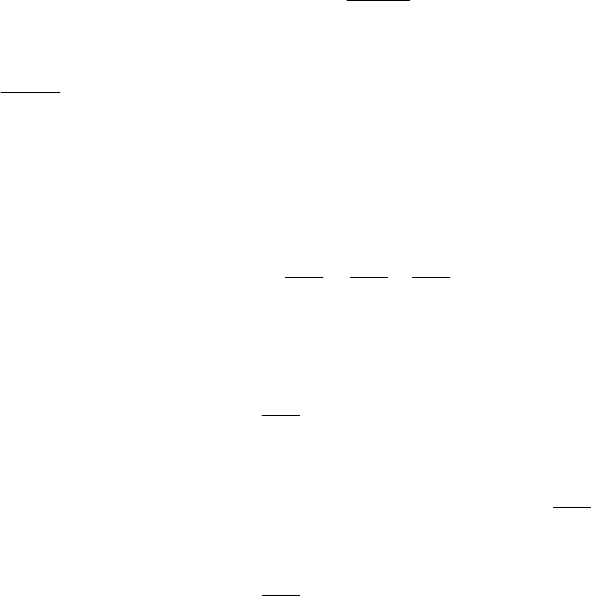
Пример 3.5. Постройте кривую седиментации и , используя аналити —
ческий метод Н . Н . Цюрупы , рассчитайте и постройте интегральную и
дифференциальную кривые распределения частиц суспензии по размерам .
Для расчёта необходимы данные о плотности ρ
и вязкости η дисперсион —
ной среды , плотности частиц ρ , высот е оседания
h и данные о кинетике се —
диментации – зависимость массы осевших частиц от времени
m=f( τ ) ( кри —
вая седиментации ).
Алгоритм решения :
Строим кривую седиментац ии m=f( τ ) ; её типичный вид представлен
на рис . 3.1. В соответствии с методом Цюрупы кривая седимент ации опи —
Источник: www.studmed.ru