Параметры элементарной ячейки золота

Элементарные ячейки являются кирпичиками кристалла. Существует всего семь типов элементарных ячеек: кубическая, тетрагональная, гексагональная, тригональная, ромбическая, моноклинная и триклинная. Эти элементарные ячейки иногда называют примитивными, или сингониями. Каждая из сингоний представлена примитивной кристаллической ячейкой.

Кроме того, существуют еще семь типов центрированных ячеек, которые содержат частицы на гранях и внутри ячейки. Всего существует 14 типов элементарных ячеек, которые называются решетками Браве, по имени французского ученого, который показал, что любую ячейку можно преобразовать в одну из 14. Чтобы выбрать ячейку, наиболее полно отражающую все особенности данной решетки, нужно придерживаться следующих правил:

симметрия ячейки должна соответствовать симметрии решетки в целом;

число прямых углов в ячейке должно быть максимальным;

объем ячейки должен быть минимальным.

·

Unit 1.8 — The Seven Crystal Systems

Объемо Кристалли́ческая структу́ра — такая совокупность атомов, в которой с каждой точкой кристаллической решётки связана определённая группа атомов, называемая мотивной единицей, причём все такие группы одинаковые по составу, строению и ориентации относительно решётки. Можно считать, что структура возникает в результате синтеза решётки и мотивной единицы, в результате размножения мотивной единицы группой трансляции.

В простейшем случае мотивная единица состоит из одного атома, например в кристаллах меди или железа. Возникающая на основе такой мотивной единицы структура геометрически весьма сходна с решёткой, но все же отличается тем, что составлена атомами, а не точками. Часто это обстоятельство не учитывают, и термины «кристаллическая решётка» и «кристаллическая структура» для таких кристаллов употребляются как синонимы, что нестрого. В тех случаях, когда мотивная единица более сложна по составу — состоит из двух или большего числа атомов, геометрического сходства решётки и структуры нет, и смешение этих понятий приводит к ошибкам. Так, например, структура магния или алмаза не совпадает геометрически с решёткой: в этих структурах мотивные единицы состоят из двух атомов.

Основными параметрами, характеризующими кристаллическую структуру, некоторые из которых взаимосвязаны, являются следующие:

• тип кристаллической решётки (сингония, решётка Браве);

• число формульных единиц, приходящихся на элементарную ячейку;

• параметры элементарной ячейки (линейные размеры и углы);

координаты атомов в ячейке;

Понятие структурный тип — один из критериев сходства или различия строения кристаллов. Обычно структурный тип относят к названию одного из веществ, кристаллизующихся в нём. Структуры кристаллов, принадлежащих к одному структурному типу, одинаковы до подобия. Структурный тип в кристаллографии определяет относительное расположение частиц (атомов или атомных групп) в кристалле, без указаний абсолютных расстояний между ними. Чтобы описать конкретную структуру, надо указать структурный тип и параметры структуры.

Лекция 9. Кристаллические решетки. Элементарная ячейка.

Структура кристалла − это конкретное расположение частиц в пространстве. Описывая структуру, необходимо указать вид и размер частиц, а также расстояния между ними. Если вещества кристаллизуются в сходных друг с другом решетках, то говорят, что они относятся к одному структурному типу. У кристаллов, принадлежащих к одному структурному типу, элементарные ячейки одинаковы с точностью до подобия. Опишем некоторые наиболее часто встречающиеся структурные типы [27, 83].

Опытные данные показывают, что почти 80 % металлов кристаллизуются в объемно- и гранецентрированных кубических, а также в гексагональных плотноупакованных решетках.

Билет 5

Источник: infopedia.su

Кристаллическая решётка. Элементарная ячейка

Структура кристалла – это конкретное расположение частиц в пространстве (физическая реальность). Чтобы представить структуру кристалла, нужно знать относительные размеры частиц, расстояния между ними, силы связи ме­жду частицами, их взаимное расположение, повторяющее расположение частиц в пространстве (пространственную решётку), и законы симметрических преоб­разований.

Симметрия – основная особенность, характерная для структуры кристаллов. Теорию строения структуры кристаллов развил английский учёный Бравэ, основываясь на многих экспериментальных результатах других исследовате­лей. Положив в основу своей теории анизотропию и симметрию кристаллов, он пришёл к понятию о пространственной решётке.

Пространственная решётка – это способ представления периодичности повторения в пространстве отдельных материальных частиц или групп частиц. Кристаллическая решётка – пространственная сетка, в узлах которой располагаются частицы (атомы, ионы, молекулы), образующие кристалл.

Основу кристалла, её остов, каркас можно представить как бесконечную решётку, со­стоящую из множества одинаковых смежных параллелепипедов — ячеек Бравэ (рис. 1.11). Например, кристаллическая решётка поваренной соли NaCl пред­ставляет собой две кубические решётки с атомами хлора и атомами натрия в узлах, «вставленные» одна в другую (рис. 1.8). Какова бы ни была кристалли­ческая решётка, описывающая структуру кристалла, в её основе всегда лежат ячейки Бравэ.

Рис. 1.11.Пространственные решётки некоторых веществ

Рассмотрим простейший случай, когда одинаковые частицы расположены в кристалле параллельными бесконечными рядами. На 1 мм в кристалле находится порядка 10 7 частиц (рис. 1.12). Трансляция (период идентичности) –симметричное преобразование, при котором точка (частица) повторяется в пространстве. Её величина – кратчайшее из возможных расстояний между одина­ковыми точками в ряду.

Рис. 1.12.Линейная цепочка атомов

Если сдвинуть точки бесконечного ряда на один период идентичности вдоль направления трансляции, то ряд совместится сам с собой, его вид не на­рушится. Выбор основных трансляций в структуре кристалла очень важен, по­тому что ими определяются кристаллографические системы координат. В об­щем случае это косоугольные координаты с разными масштабными отрезками по осям (рис. 1.13).

Узлы ряда – одинаковые точки, связанные между собой величиной трансляции а в бесконечном ряду. При перенесении точек по трём направлениям на величину трансляций а, b, c можнополучить трёхмерную сетку.

Ячейки сетки – параллелограммы, вершины которых являются узлами.

Элементарная ячейка – параллелепипед с характерным для данной решётки расположением частиц, с помощью которого весь кристалл может быть построен путём его многократного повторения в трёх направлениях. Она стро­ится на трёх элементарных трансляциях а, b, с. Элементарную ячейку принято выбирать так, чтобы она удовлетворяла следующим условиям: наилучшим об­разом отражала симметрию сетки, имела бы прямые углы и, если возможно, обладала бы наименьшим объёмом.

Примитивной называется элементарная ячейка, внутри которой нет узлов, частицы содержатся только в вершинах (рис. 1.13). Узлы решётки – вершины ячеек, в которых располагаются одинаковые атомы или группы атомов. Они эк­вивалентны друг другу.

Период (постоянная) кристаллической ячейки – расстояние между однородными атомами. Параметры элементарной ячейки: три ребра ячейки a, b, c; три угла между ними α, β, γ. Например, для представленной на рис. 1.13 примитивной ячейки, соотношения между параметрами следующие:

Рис. 1.13.Примитивная элементарная ячейка

Элементарные ячейки, составляющие кристаллическую решётку кристалла, имеют одинаковые форму и объём. Кристалл можно построить с помощью разных примитивных ячеек. В некоторых случаях удобно характеризовать про­странственную сетку не примитивной, а сложной элементарной ячейкой, у ко­торой узлы есть не только в вершинах, но и внутри ячейки. Элементарная ячей­ка может содержать несколько примитивных ячеек.

Элементарные ячейки различаются по элементам симметрии и степени заполнения атомами (рис. 1.14).

Рис. 1.14.Разные примитивные ячейки в плоской сетке

К элементам симметрии относятся: трансляции, плоскости симметрии, зеркальные плоскости, оси симметрии разных порядков, инверсионные оси симметрии (рис. 1.15).

Рис. 1.15. Элементы симметрии в кубическом кристалле

Кристаллические ячейки делятся по элементам симмет­рии на 7 сингоний: триклинная, моноклинная, ромбическая, ромбоэдрическая, гексагональная, тетрагональная, кубическая. Сингония в дословном переводе – сходноугольность. В сингонию объединяют кристаллы, у которых одинакова симметрия элементарных ячеек и одинаковая система координат. На рис. 1.16 показана тетрагональная ячейка.

Рис. 1.16. Кристаллическая ячейка тетрагональной сингонии

В каждой сингонии элементарные ячейки делятся по степени заполнения их атомами. Так на одну ячейку простой кубической ячейки имеет приходится 1 атом: n = (1/8)8 = 1; объёмноцентрированной кубической ячейки (ОЦК) – 2 атома: n = (1/8)8 + 1 = 2; гранецентрированной кубической ячейки (ГЦК) – 4 атома: n =(1/8)8 + (1/2)6 = 4 Рис. 1.17); гексагональной с плотной упаковкой (ГПУ) – 2 атома.

Рис. 1.17. Кристаллические ячейки

Кристаллическую решетку общего типа называют решеткой с базисом (БЦК). Решетка с базисом представляется в виде двух вставленных одна в другую подрешеток Бравэ, каждая из которых определяется трансляцион­ными векторами. Базисный вектор устанавливает смещение реше­ток друг относительно друга. Количество базисных векторов может быть сколь угодно большим.

Рис. 1.18.Решётки Браве

Все известные в природе кристаллические тела кристаллизуются в 14 ре­шётках Браве (рис. 1.18). Далее они делятся на 32 класса симметрии и 230 пространственных групп.

Некоторым телам свойственна не одна, а две или более кристаллических структур, устойчивых при различных температурах и давлениях. Такое явление называется полиморфизмом. Полиморфные формы (модификации вещества) имеют, например, углерод и олово. Углерод может существовать в виде алмаза и графита. Алмаз очень прочный и твёрдый, графит – хрупкий.

Элементарные ячейки алмаза и графита относятся к различным сингониям (рис. 1.19).

Рис. 1.19.Кристаллические решётки алмаза и графита

Олово может существовать в виде двух модификаций – серого и белого. Серое олово при температурах ниже 13,3 °С. имеет решётку типа алмаза. При температурах выше 13,3 °С серое олово превращается в белое олово – очень хрупкое вещество, которое легко разрушается в порошок. Белое (металличе­ское) олово имеет тетрагональную объёмноцентрированную решётку.

Полиморфные модификации обозначают греческими буквами: α, β, γ. начиная с самой низкой температуры. Переход от одной модификации к другой сопровождается выделением или поглощением скрытой теплоты превращения. Полиморфное превращение является фазовым переходом 1-го рода. Полимор­физм имеет важное практическое значение: это свойство используется при термической обработке сталей, придании сталям различных свойств, получении нержавеющих сталей.

ИНДЕКСЫ МИЛЛЕРА

Для описания кристаллических многогранников и структур применяется метод индицирования. Через узлы кристаллической решетки можно провести прямые линии и плоскости. Выберем один из узлов решётки за начало координат.

Любой другой узел решётки определяется радиус–вектором:

R = m a + n b + р с.

Индексы узла – три простых числа [[mnp]], взятые в двойные квадратные или фигурные скобки (рис. 1.20). В системе параллельных прямых всегда можно выделить прямую линию (ряд), проходящую через начало координат. Тогда направление прямой линии определится двумя точками: началом координат и любым узлом ряда.

Индексы направления (прямой линии) – три простых числа [mnp], взятые в квадратные скобки. Эти числа характеризуют положение ближайшего узла, лежащего на прямой линии, проходящей через начало координат.

Рис. 1.20.Миллеровские индексы узлов

Проходящая сквозь узлы прямая, а также ребро кристаллического многогранника имеют наклон в выбранной системе координат. В целом плоские сет­ки в пространственной решётке и соответствующие им грани кристаллического многогранника имеют наклон в системе координат.

Пусть некоторая плоскость решётки пересекает все три оси координат, отсекая на них отрезки ma, nb, pc. Отношение чисел m:n:p характеризует наклон плоскости к осям координат. Серию отношений рациональных чисел m:n:p для всех параллельных плоско­стей можно заменить отношением взаимно простых чисел р:q:r. Числа р, q, r называются параметрами Вейса.

Миллеровские индексы плоскости – три простых числа (HKL), записанные в круглых скобках. Индексы плоскости – дополнительные множители к величинам, обратно пропорциональным числу осевых единиц, отсекаемых лю­бой плоскостью данного семейства на координатных осях Х, У, Z.

Миллеровские индексы опреде­ляются из соотношения чисел р:q:r.

Пусть некоторая плоскость отсекает на осях координат отрезки:

р =1, q = 3, c = 2 (рис. 1.21). Составим отношения:

Общий знаменатель равен 6. Дополнительные множители: H = 6, K = 2, L = 3.

Миллеровские индексы данной плоскости (623).

Рис.1.21. Индексы плоскости(623)

Межплоскостное расстояние – это расстояние между параллельными плоскостями, содержащими одинаковое количество атомов. Чем больше индексы H, K, L, тем меньше расстояние между плоскостями. Для кубического кристалла межплоскостное расстояние d для параллельных плоскостей с одинаковыми индексами выражаются через индексы этих плоскостей соотношением:

а– постоянная решётки.

В 1819 г. Гаюи сформулировал закон целых чисел (теперь закон Гаюи): для любых двух граней реального кристалла двойные отношения параметров равны отношению малых чисел. На кристаллографическом многограннике образуются лишь такие грани, для которых двойные отношения отрезков, отсекаемых данной гранью и еди­ничной гранью на трёх рёбрах кристалла, принятых за оси координат, равны отношению целых небольших простых чисел.

Грани, для которых отношение р:q:r является иррациональным, в реальном кристалле невозможны. Наклон всякой грани можно определить тремя целыми числами, если за оси координат выбрать направление трёх рёбер кристалла, а за параметры – отрезки, отсекае­мые на этих осях данной гранью.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник: studopedia.ru

Элементарная ячейка кристаллической решетки: определение и виды

Элементарная ячейка кристаллической решетки служит для описания микроструктуры материалов. От ее параметров зависят многие физико-химические свойства вещества: твердость, температура плавления, электро- и теплопроводность, пластичность и другие. Типы этих элементарных структур были описаны еще в 19 веке. Одной из разновидностей является примитивная ячейка. Для выделения в структуре материала элементарной ячейки необходимо соблюдение ряда условий.

Кристаллическая решетка

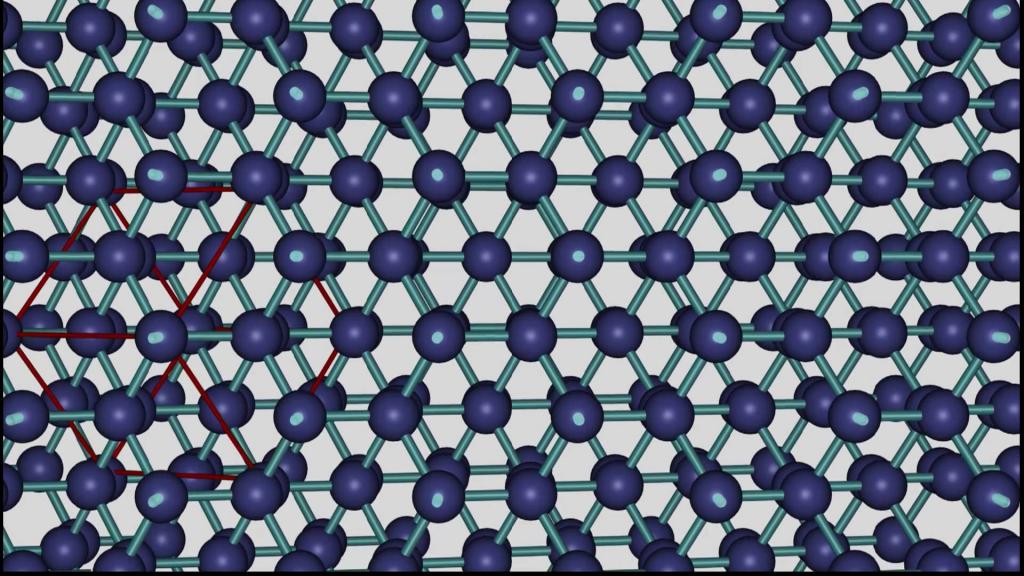
Все твердые тела по внутренней структуре можно классифицировать на две формы: аморфные и кристаллические. Отличительной особенностью последних является специфическая организованная структура частиц.

Кристаллическая решетка – это упрощенная трехмерная модель твердых кристаллов, которая используется для анализа их свойств в физике, химии, биологии, минералогии и других науках. Внешне она похожа на сетку. В ее узлах находятся атомы вещества. Данный массив точек имеет определенный, регулярно повторяющийся порядок, специфичный для каждого вида вещества.

Что такое элементарная ячейка?

Элементарная ячейка кристаллической решетки – это наименьшая часть твердого тела, которая позволяет охарактеризовать его свойства. Она служит основой решетки и дублируется в ней бесчисленное количество раз.

Данная модель используется для упрощения визуального описания внутреннего строения кристаллов. При этом применяется система из 3 кристаллографических координатных осей, которые отличаются от обычных ортогональных тем, что они являются конечными отрезками определенного размера. Углы между осями могут быть равны 90° или быть непрямыми.

Если плотно заполнить элементарными ячейками определенный объем, то можно получить идеальный монокристалл. На практике более распространены поликристаллы, состоящие из нескольких ограниченных в пространстве регулярных структур.

Виды

В науке выделяют 14 видов элементарных ячеек решеток, обладающих уникальной геометрией. Впервые их описал французский физик Огюст Бравэ в 1848 г. Этого ученого считают основателем кристаллографии.

Данные типы элементарных структур кристаллической решетки группируют в 7 категорий, называемых сингониями, в зависимости от соотношения длин сторон и равенства углов:

• кубическая;
• тетрагональная;
• орторомбическая;
• ромбоэдрическая;
• шестиугольная;
• триклинная.

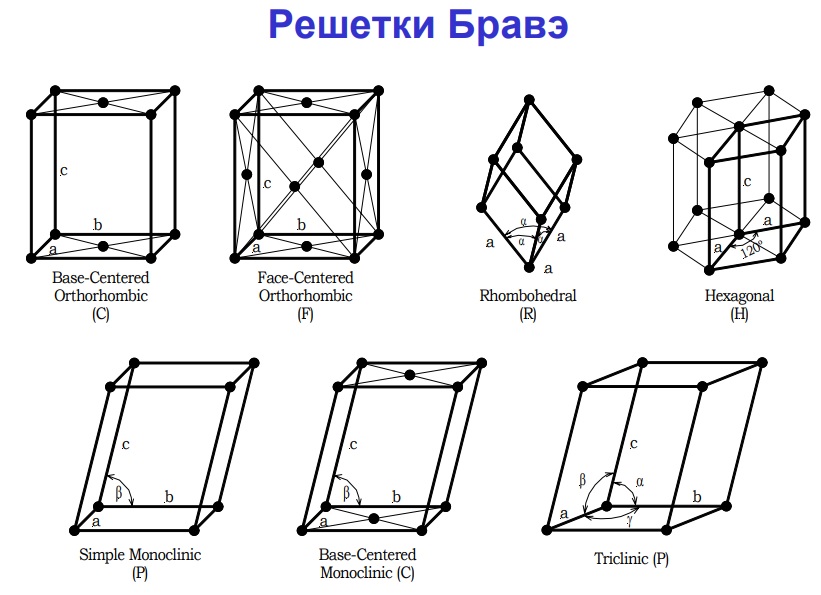
Наиболее простой и распространенной в природе из них является первая категория, которая в свою очередь делится на 3 типа решеток:

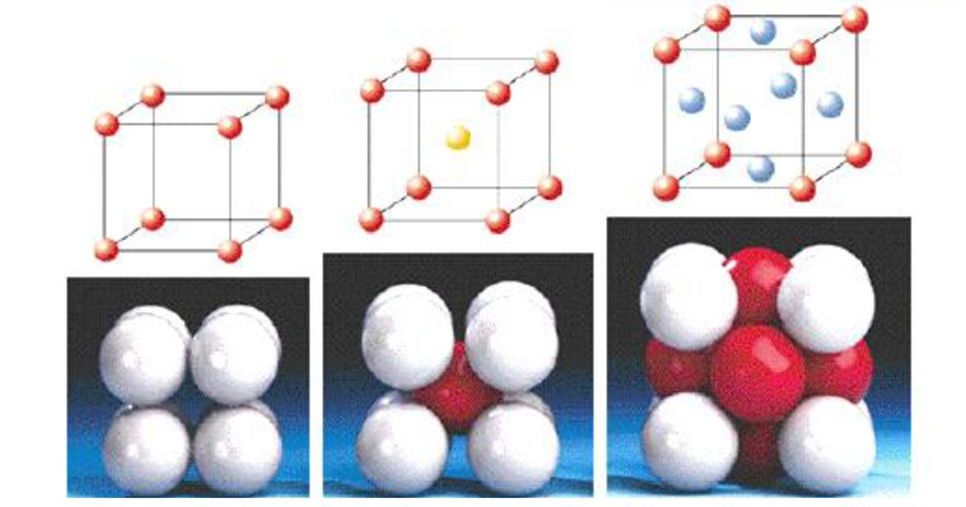
• Простая кубическая. Все частицы (а ими могут быть атомы, электрически заряженные частицы или молекулы) находятся в вершинах куба. Эти частицы идентичны. Каждой ячейке принадлежит 1 атом (8 вершин × 1/8 атома = 1).
• Объемноцентрированная кубическая. Отличается от предыдущей модели тем, что в центре куба находится еще одна частица. К каждой ячейке относится по 2 атома вещества.
• Гранецентрированная кубическая. Частицы содержатся в вершинах элементарной ячейки, а также в центре всех граней. Каждая из ячеек насчитывает по 4 атома.

Примитивная ячейка

Элементарная ячейка называется примитивной, если ее частицы находятся только в вершинах решетки и отсутствуют в других местах. Ее объем является минимальным по сравнению с другими типами. На практике она оказывается часто низкосимметричной (примером может служить ячейка Вигнера-Зейтца).

У не примитивных ячеек атом в центре объема делит их на 2 или на 4 одинаковые части. В гранецентрированной структуре происходит разделение на 8 частей. В металлографии пользуются понятием элементарной, а не примитивной ячейки, так как симметрия первой позволяет более полноценно описать кристаллическую структуру материала.

Признаки

Все 14 видов элементарных ячеек обладают общими свойствами:

• они являются простейшими повторяющимися структурами в кристалле;
• каждый центр решетки состоит из одной частицы, называемый узлом решетки;
• узлы ячейки соединяются между собой прямыми, которые формируют геометрию кристалла;
• противоположные грани параллельны;
• симметрия элементарной структуры соответствует симметрии всей кристаллической решетки.

При выборе структуры элементарной ячейки руководствуются некоторыми правилами. У нее должны быть:

• наименьший объем и площадь;
• наибольшее количество одинаковых ребер и углов между ними;
• прямые углы (по возможности);
• пространственная симметрия, отражающая симметрию всей кристаллической решетки.

Объем

Объем элементарной ячейки определяется в зависимости от ее геометрической формы. Для кубической сингонии он вычисляется как длина грани (межцентровое расстояние атомов), возведенная в третью степень. Для гексагональной сингонии объем можно определить по формуле, указанной ниже:

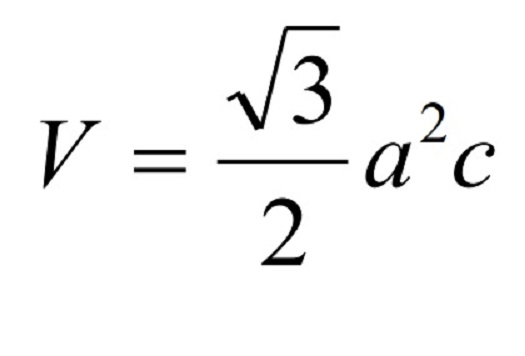
где a и c – параметры кристаллической решетки, измеряющиеся в ангстремах.

На практике параметры кристаллической решетки рассчитываются для того чтобы в дальнейшем можно было определить структуру соединения, массу атома (исходя из веса данного объема и числа Авогадро) или его радиус.

Источник: fb.ru