Золото один из самых желанных драгоценных металлов на Земле. Используется не только в производстве украшений, но и в различных областях науки, при производстве техники, различного оборудования. Золото в чистом виде применяется редко, так как это мягкий, пластичный материал. Обычно его смешивают с другими металлами и получают сплавы.
В ювелирных украшениях качество оценивают по содержанию золота в изделии. Для этого применяют пробу в виде клейма. Проба 999 — означает практически чистое золото, без примесей.
На золотых украшениях по большей части встречаются пробы — 585 и 583 пробы. 585 проба означает, что в изделии 58,5% золота и 41,5% примесь других металлов. Обман в производстве золотых украшений заключается в указании, например 585 пробы, а по существу золота будет в разы меньше. Встречаются и полные подделки, когда в изделии вообще нет ни процента золота. Как же определить, золото перед вами или нет?
Характеристики золота
Драгоценное золото — это тяжёлый металл. Его плотность в чистом виде составляет 19 621 кг/м³. Чтобы воспринимать сухой факт как можно ярче, представьте небольшой шарик из чистого металла с диаметром 46 мм. Его масса будет равна 1 килограмму.
Проверка золота методом гидростатического взвешивания
Высокая плотность золота используется и в его добыче: именно благодаря ей самородки и песок можно отсеять от пород промывкой.
Плотность золота в чистом виде (том, которое принято считать 999,99-й пробой) 19,3 г/см3. Самородное, оно имеет нескольку меньшую плотность: 18-18,5 г/см3. В сплавах разных проб этот показатель свой. О них мы расскажем далее.

Гидростатическое давление и архимедова сила
Причиной появления выталкивающей силы, действующей на помещенное в жидкость абсолютно любое твердое тело, является гидростатическое давление. Оно вычисляется по формуле:
Где h и ρl — глубина и плотность жидкости соответственно.
Когда тело погружают в жидкость, то отмеченное давление действует на него со всех сторон. Суммарное давление на боковую поверхность оказывается равным нулю, а вот давления, приложенные к нижней и верхней поверхностям, будут отличаться, поскольку эти поверхности находятся на разной глубине. Такая разница приводит к появлению выталкивающей силы.

Согласно закону Архимеда погруженное тело в жидкость вытесняет вес последней, который равен выталкивающей силе. Тогда можно записать формулу для этой силы:
Символом Vl обозначен объем жидкости, вытесненной телом. Очевидно, что он будет равен объему тела, если последнее в жидкость погружено полностью.
Сила Архимеда FA зависит только от двух величин (ρl и Vl ). Она не зависит от формы тела или от его плотности.
Плотность сплавов золота
Как мы знаем еще из школьного курса, плотность материала — физическое свойство, определяемое как масса взятой единицы объема. Измеряется она через соотношение массы тела и его величины.
Получение реактива на золото. В домашних условиях легко!
Для получения пригодных к использованию в ювелирном производстве сплавов золото смешивают с медью, серебром, никелем, платиной, палладием и прочими металлами, как благородными так и нет. Перейдем же к данным о плотности сплавов золота разной пробы.
Самая популярная, доступная по цене и отлично подходящая для работы с ней, — 585-я проба. Плотность золота 585-й пробы — 12,5-14 г/см3. Эти же рамки определяются и 583-ю пробу (советского образца).
Для монетных проб, 900-й и 917-й, показатели равны, соответственно, 17,10-17,24 г/см3 и 17,34-17,83 г/см3.
Так же часто встречающаяся проба в ювелирных изделиях 750-я имеет плотность 14,5-17,5 г/см3.
Плотность низкопробного золота, 375-й пробы, — 11,54-11,56 г/см3.
И, наконец, вспомним о другом благородном металле — серебре. Оно значительно легче золота, и плотность серебряных сплавов также ниже.
Так, плотность самого распространенного в изделиях сплава 925-й пробы составляет 10,36 г/см3. Второго по используемости, 875-й пробы, — 10,28 г/см3.
Как проверить золото в домашних условиях
Существует несколько методов:
Выше перечисленные методы, для определения золота в домашних условиях, годятся лишь для отличий грубой подделки. Лучше всего подойдет метод с использованием йода и нашатыря. Для определения примесей, годятся лабораторные испытания или можно обратиться в ломбард.
Проверка уксусом — миф, не рабочий метод.




Гидростатический метод: определяем пробу драгоценного сплава
В учреждениях, специализирующихся на приеме золотых изделий, применяется множество различных способов определения и подтверждения пробы принесенного золота. На основе знания о том, что золото — металл тяжелый с большой плотностью, был введен в использование гидростатический метод.
Он основан на определении разницы в весе при измерении показателей на открытом воздухе, в обычных условиях, и в жидкости с наверняка известной плотностью.
Оговоримся сразу: такой метод проверки золота подходит лишь для целостных изделий, без камней и прочих вставок из других материалов. Также невозможно получить адекватные данные об изделиях полых, состоящих из многих подвижных деталей.
Для проведения гидростатического взвешивания золотого изделия понадобятся ювелирные весы, мерный стакан (или любой другой прозрачный), леска или тонкая нитка. В качестве жидкости с известной плотностью обычно используется дистиллированная вода. Сначала золотое изделие взвешивается обычным методом, данные фиксируются.
Затем на весы ставится стакан с водой, наполненный более чем наполовину, показания весов обнуляются (на весах должна быть функция обнуления веса тары). Наше золотое изделие, подвешенное на леске, опускается в воду полностью, при этом не касаясь дна и стенок стакана. Данные весов также фиксируются.
Для анализа плотности лучше использовать гидростатический калькулятор, поскольку просчет вручную займет гораздо больше времени и не настолько точен.

Как проверяют золото в ломбарде
Скупщики золота, проверяют золотые украшения кислотами. Сначала проводят золотом по пробирному камню (кремниевый сланец), и в зависимости от пробы на изделии, применяют определенную кислоту. На камне остается чуточку металла, на него и капают каплю кислоты. Подделка испарится под действием кислоты, а следы от настоящего золота останутся на месте.
Первое, что делают в ломбарде — осматривают пробу. Она должна быть четкая по всем углам, и иметь клеймо завода изготовителя. Потом специалист прикладывает украшение к магниту. Это такой быстрый метод исключить грубую подделку. Золото не магнитится, а если другой металл покрыли позолотой, то он притянется к магниту.
Ну а потом уже специалист использует химию, для определения качества изделия.

Выводы
Итак, в нашей статье мы рассмотрели плотность золота — драгоценного металла, с которым каждый из нас в жизни сталкивался и еще столкнется. Резюмировать приведенные данные можно следующим образом: плотность самой популярной пробы золота, 585-й, составляет 12,5-14 г/см3, у других сплавов — меньшая или большая соответственно.
По плотности золотого сплава можно определить пробу, что является показателем содержания чистого золота в сплаве. Эти методы используются в учреждениях, занимающихся приемом золота.
Надеемся, наша статья была познавательной и подарила вам несколько увлекательных минут. Пусть в вашей шкатулке будет только настоящее высокопробное золото!
Что собой представляют гидростатические весы?
В конце XVI века их изобрел Галилей. Схематическое изображение весов показано на рисунке ниже.

По сути, это обычные весы, принцип работы которых основан на равновесии двух рычагов одинаковой длины. На концах каждого рычага имеется чашечка, где можно размещать грузы известной массы. Снизу одной из чашечек прикреплен крючок. Он применяется для подвешивания грузов. В комплекте с весами также идет стеклянный стакан или цилиндр.
На рисунке буквами A и B отмечены два металлических цилиндра равного объема. Один из них (A) является полым, другой (B) — сплошным. Эти цилиндры используют для демонстрации закона Архимеда.
Описанные весы используют для определения плотности неизвестных твердых тел и жидкостей.

Использование магнетизма
Золото также отличается от других металлов своей магнитной проницаемостью. Этот драгметалл относится к диамагнетикам (отталкивается магнитом) в отличие от вольфрама, который является парамагнетиком (его можно притянуть магнитом). Поэтому, при воздействии магнита на изделия из чистого золота они должны слабо отталкиваться.
Чтобы повысить точность определения подлинности золота в монетах с помощью этого метода, можно воспользоваться специальными магнитными весами. Они достоверно покажут отталкивающие или притягивающие магнитные свойства предмета. Обычно к подобным измерительным приборам прилагаются табличные значения величин, соответствующие некоторым золотым монетам и слиткам. Данный метод исследования вполне применим даже к слитковому золоту в специальной оболочке.
Что в итоге
Для доказательства подлинности 24-каратных золотых монет и слитков вполне можно обойтись исследованием удельного веса изделия. Данный метод позволит отсеять некачественные фальшивки. Но если мы имеем дело с золотом еще меньшей пробы или слитковым драгметаллом в оболочке, придется воспользоваться более дорогостоящими методами экспертизы. Добросовестный продавец никогда не станет препятствовать покупателю в его желании убедиться в качестве приобретаемой продукции любыми из описанных способов.
В данной публикации не рассматриваются способы исследования поверхностных свойств золота в монетах, таких как рентгеновская флуоресценция и спектрометрия, поскольку они способны определить подлинность золота лишь в случае доказанной однородности предмета. Кроме того, их желательно применять по всей поверхности изделия, чтобы исключить наличие местных неоднородностей. Дополнительно по теме: как отличить подлинную золотую монету от поддельной можно здесь.
Источник: cherish-centr.ru
Астрономический словарик: гидростатическое равновесие, горизонт событий, гравитационное линзирование

Впервые термин ввели физики для описания состояния жидкостей, в котором действующие на неё силы уравновешиваются. В таком случае жидкость находится в состоянии покоя. На поверхности Земли, например, это может быть равновесие силы тяжести, действующей на жидкость, и силы давления самой жидкости, возникающей из-за межмолекулярных взаимодействий.
Однако в подобных терминах можно описывать не только жидкости. Например, взаимодействие молекул газов, составляющих воздух, препятствует гравитации Земли, стремящейся сплюснуть атмосферу. А гравитация не даёт этому взаимодействию выбросить нашу атмосферу в открытый космос.
Похожими способами можно описать и изучать скалистые планеты, а также звёзды, межзвёздные облака газа и пыли и даже звёздные скопления. Например, по определению, принятому Международным астрономическим союзом в 2006 году, планету от других небесных тел отличает то, что её гравитация преодолевает сопротивление материала, из которого она состоит, что придаёт ей эллипсоидную форму, и делает состав переменным по мере погружения от поверхности к центру. Говорят, что планета находится в гидростатическом равновесии.
Звёзды находятся в гидростатическом равновесии, поскольку внутреннее давление тепла и излучения, направленное наружу, компенсируется гравитацией их вещества. Если звезда вращается, она может оставаться в гидростатическом равновесии до определённой максимальной скорости вращения – при этом из-за центробежных сил вращающееся небесное тело на экваторе имеет больший диаметр, чем тот, что соединяет его полюса. Чем больше энергии выделяется в процессе синтеза, тем больше звезда расширяется. Когда у неё заканчивается топливо, она начинает сжиматься.
Плазма, заполняющая звёздные скопления, до достижения определённой массы поддерживает себя в гидростатическом равновесии благодаря высокой температуре, которая не даёт ей схлопнуться.
Горизонт событий

Прямое изображение чёрной дыры в центре галактики Мессье 87
Массивные тела притягиваются друг к другу. Чтобы одному телу вырваться из гравитационного притяжения другого, ему необходимо набрать определённую скорость. Чтобы космическая ракета смогла не просто выйти на орбиту вокруг Земли, но отправиться в открытый космос, ей надо набрать т.н. «вторую космическую скорость» или «скорость убегания». Она рассчитывается по формуле:
Где G – гравитационная постоянная, R – расстояние от центра планеты до тела, а M – её масса. Чем больше масса планеты, тем большую скорость нужно набрать для того, чтобы высвободиться из её гравитационного захвата. На Луне это 2,3 км/с, на Земле – 11,2 км/с, на Юпитере – 60 км/с, на Солнце – 617,5 км/с. Однако в своей Специальной теории относительности Эйнштейн постулировал существование максимальной скорости – скорости света в вакууме.
Получается, что небесное тело может набрать такую массу, при которой, попав на его поверхность (а точнее, приблизившись на определённое расстояние к его центру), ничто, даже свет, не сможет больше убежать обратно в космос. Для этого тело должно быть одновременно массивным и достаточно компактным (поскольку, чем больше расстояние до центра, R, тем меньше будет скорость убегания). До этого ещё в 1784 году додумался Джон Мичелл — священник из английской деревни, естествоиспытатель, геолог и астроном. Он назвал подобные гипотетические объекты «тёмными звёздами».
И такие тела существуют в реальности – это чёрные дыры. В начале XX века Эйнштейн показал, что гравитация влияет на движение света. Затем Карл Шварцшильд решил уравнения Эйнштейна для точечной и сферической масс. Так появилось понятие радиус Шварцшильда – расстояния от центра объекта, на котором вторая космическая скорость совпадает со скоростью света. Американский физик Вольфганг Риндлер предложил называть сферу такого радиуса «горизонтом событий», а физик-теоретик Дэвид Финкельштейн в 1958 году впервые определил термин «чёрная дыра» как область в пространстве, которую ничто не может покинуть.
С чёрными дырами и горизонтом событий связано несколько парадоксов физики – противоречий, способа разрешения которых мы не знаем. Например, внутри горизонта событий находится «сингулярность» — место, в котором некоторые члены уравнения Эйнштейна становятся бесконечными (к примеру, кривизна пространства-времени). Кроме того, сочетание квантовой механики и общей теории относительности приводит к информационному парадоксу, возникающему вблизи горизонта событий.
В 1970-х годах Стивен Хокинг показал, что чёрная дыра должна испускать фотоны, причём параметры этого излучения определяются исключительно её массой, зарядом и моментом импульса. При этом благодаря такому излучению чёрная дыра способна за достаточно долгое время полностью «испариться». Получается, что вся остальная физическая информация о веществе, упавшем в чёрную дыру, бесследно исчезает.
Однако это противоречит одному из основных принципов физики – что состояние системы в один момент времени должно определять её последующие состояния в будущем. В частности, в квантовой физике состояние системы описывается волновой функцией, а её изменение во времени – унитарным оператором. Унитарность предполагает, что по взятой в любой момент времени волновой функции можно определить значение этой функции в прошлом или будущем.
В 1997 году было сделано предположение о наличии связи между теориями, описывающими квантовую гравитацию в терминах теории струн, и теориями квантового поля — АдС/КТП соответствие. Это предположение позволяет считать, что информация при испарении чёрных дыр всё-таки сохраняется. Фанаты теории струн считают, что излучение Хокинга не является строго тепловым – в нём содержатся небольшие квантовые коррекции, кодирующие информацию о материи, попавшей в чёрную дыру. Любители петлевой квантовой гравитации считают, что информация до последнего хранится в чёрной дыре, и освобождается в самые последние моменты её испарения, когда на её эволюцию уже начинают влиять квантовые эффекты.
Часть физиков вообще считает, что ничего плохого в нарушении унитарности нет, и в присутствии гравитации квантовые системы и так ведут себя неунитарно.
Также в космологии горизонтом событий называют максимальное расстояние до объекта, свет от которого, испущенный в данный момент, сможет дойти до нас в будущем. Из-за постоянного расширения Вселенной все гравитационно не связанные с нашей системой объекты удаляются от нас – и чем дальше находится объект, тем быстрее он удаляется. В итоге достаточно далёкие объекты удаляются от нас со скоростью, превышающей скорость света (что не нарушает специальную теорию относительности, ограничивающую максимальную скорость только для локальных систем). Поэтому света от некоторых объектов мы не сможем увидеть уже никогда.
Гравитационное линзирование
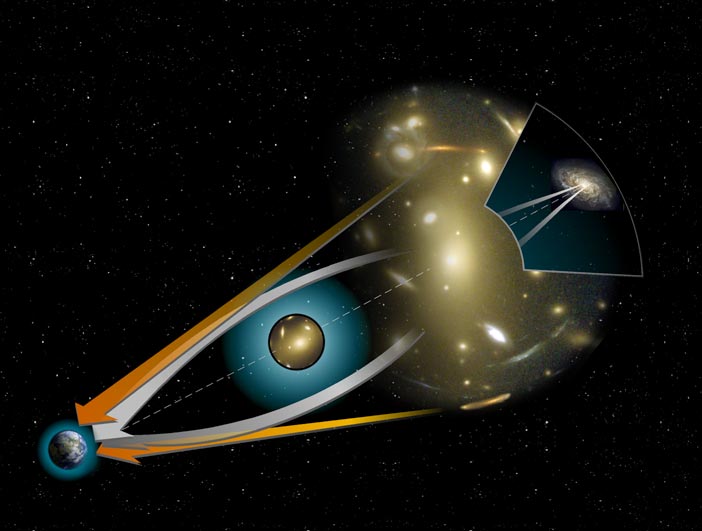
На стыке XVI и XVII веков Ньютон описал закон всемирного тяготения. С его точки зрения сила гравитации действовала мгновенно и на любом расстоянии на все тела, обладающие массой, притягивая их друг к другу. Уже он задался вопросом (в своей книге «Вопросы», где перечислил нерешённые на тот момент научные задачи): не могут ли массивные тела притягивать свет?
Через сто лет после этого видные учёные того времени, Генри Кавендиш (занимавшийся в основном исследованием газов) и Иоганн фон Зольднер (астроном, физик и математик), согласились, что так оно и должно быть – в то время преобладала корпускулярная теория света, по которой свет представлял собой поток элементарных частиц. Последний даже рассчитал угол отклонения луча света под воздействием массивного тела. Позднее, в 1911 году такой же результат, как у него, получил Эйнштейн – только он рассчитывал этот угол, исходя исключительно из принципа гравитационного замедления времени. Чуть позже Эйнштейн разработал Общую теорию относительности, согласно которой рассчитанные ранее им и фон Зольднером результаты были в два раза меньше нужного.
И это было блестяще подтверждено 29 мая 1919 года во время солнечного затмения. Поскольку Солнце было закрыто Луной, можно было наблюдать за светом звёзд, приходящим к нам.
И звезда, находившаяся на небосводе недалеко от Солнца, действительно оказалась немного «не на своём месте» — гравитационное искривление пространства привело к тому, что свет от звезды отклонился от прямой линии. Это экспериментальное подтверждение так поразило общественность, что новости о нём попали на первые полосы крупнейших газет мира. Именно после этого Эйнштейна и его ОТО постигла мировая слава. Когда ассистент спросил учёного, что было бы, если бы его расчёты не подтвердились, Эйнштейн ответил: «Мне стало бы жаль господа Бога. Но моя теория верна в любом случае».
Угол отклонения света определяется по формуле:
Где М – масса объекта, G – гравитационная постоянная, r – расстояние до центра объекта.
Сам Эйнштейн предположил, что из-за искажения света от источника можно будет наблюдать несколько его «копий», благодаря тому, что свет будет обтекать массивное тело с разных сторон. Однако первым на эту тему опубликовал работу Орест Данилович Хвольсон, российский и советский учёный-физик и педагог, член-корреспондент Петербургской академии наук, почётный член Российской академии наук. В короткой статье «О ложной двойной звезде» в журнале «Astronomische Nachrichten» 1924 года он описал своё предвидение кольцевидной формы изображения источника света при гравитационном линзировании. В 1936 году Эйнштейн опубликовал свою статью, где вычислил радиус такого кольца.
В 1937 году астрофизик Фриц Цвикки предположил, что открытые незадолго до этого галактики могут быть как источником света, так и гравитационной линзой. В 1963 году несколько астрофизиков независимо предположили, что идеальным источником света для наблюдения гравитационного линзирования должны быть квазары.
Но впервые этот эффект удалось пронаблюдать только в 1979 году. Изображение квазара Twin QSO выглядело раздвоенным благодаря галактике YGKOW G1, расположенной непосредственно между Землей и квазаром. С 1980-х годов благодаря распространению ПЗС-матриц и компьютерной обработки изображений эффект гравитационного линзирования стали наблюдать регулярно.
Словарик
Абсолютная звёздная величина
Адаптивная и активная оптика
Альбедо
Астрономическая единица
Барионные акустические осцилляции
Белый карлик
Быстрый процесс захвата нейтронов
Галактические скопления
Галактическое гало
Галилеевы спутники
Гелиосфера
Гидростатическое равновесие
Горизонт событий
Гравитационное линзирование
Гравитация
Диаграмма Герцшпрунга — Рассела
Закон Хаббла
Затменные звёзды
Звезда Вольфа — Райе
Зодиакальный свет
Ионосфера
Квазар
Кома
Коричневый карлик
Космическая скорость
Космические лучи
Красный карлик
Магнетар
Межзвёздная среда
Местная группа
Молекулярные облака
Нейтрино
Нейтронная звезда
Неправильная галактика
Новая звезда
Параллакс
Парсек
Планета
Планетарная туманность
Полярное сияние
Приливный разогрев
Протопланетный диск
Радиационный пояс
Рассеянное звёздное скопление
Реликтовое излучение
Сверхновая типа Ia
Сверхновая типа II
Светимость
Сильное взаимодействие
Слабое взаимодействие
Спектр
Стандартные свечи
Тёмная материя
Тёмная энергия
Тень и полутень
Теория Большого взрыва
Транснептуновый объект
Хромосфера
Цефеиды
Червоточины
Чёрные дыры
Шаровые скопления
Щели Кирквуда
Эксцентриситет орбиты
Электромагнетизм
Эллиптическая галактика
Эффект Доплера
- гидростатическое равновесие
- горизонт событий
- гравитационное линзирование
- астрономический словарик
- Научно-популярное
- Физика
- Астрономия
Источник: habr.com
Экспериментальная проверка основного закона гидростатики: Методические указания к лабораторной работе

Экспериментальная проверка основного закона гидростатики: Методические указания к лабораторной работе / Сост.: А.В. Космынин, А.Д. Бурменский, О.А. Красильникова. — Комсомольск-на-Амуре: ГОУВПО КнАГТУ, 2005. — 7с.
Даны необходимые сведения о силах, действующих на тело, погруженное под слой жидкости. Описана лабораторная установка. Описан порядок проведения эксперимента и представлены основные расчетные формулы.
Рекомендуется для студентов специальностей 140100, 140200, 550900, 120100 и 120300.
Печатается по постановлению редакционно-издательского совета ГОУВПО «Комсомольский-на-Амуре государственный технический университет»
Согласовано с отделом стандартизации
Рецензент В.С. Виноградов
Редактор Е.О. Колесникова
Подписано в печать
Формат 60 х 84 1/16. Бум. тип. №3. Печать офсетная.
Усл. печ. л. Уч.-изд. л. Тираж 100. Заказ . Бесплатно.
Редакционно-издательский отдел Государственного образовательного
учреждения высшего профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
681013, Комсомольск-на-Амуре, пр. Ленина, 27
Полиграфическая лаборатория Государственного образовательного
учреждения высшего профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
681013, Комсомольск-на-Амуре, пр. Ленина, 27
Цель работы: рассмотреть способ применения основного закона гидростатики для определения силы давления жидкости на плоскую фигуру.
1. ОБЩИЕ ПОЛОЖЕНИЯ
Силы, действующие на жидкость, подразделяются на внутренние и внешние.
Внутренние силы возникают внутри рассматриваемого объёма жидкости. К их числу относятся силы давления и трения.
Под внешними силами понимают силы, приложенные к рассматриваемому объему со стороны других тел. Внешние силы, в свою очередь, подразделяются на поверхностные и массовые (объемные). К массовым силам относятся; собственный вес жидкости, сила инерции, силы электромагнитного поля, если жидкость электропроводна и т.д.
К поверхностным силам относятся: сила трения и сила давления, действующие на поверхность рассматриваемого объема.
В общем случае внешняя сила DR действует на площадку DS под некоторым углом. Силу DR можно разложить на две составляющие: нормальную DF и тангенциальную DТ (рисунок 1). Сила DF обуславливает силу давления, а DТ — силу трения.
При уменьшении элементарной площадки DS будет изменяться и сила DF. При этом, если рассмотреть предел
то он будет иметь определенное значение р, называемое гидростатическим давлением в точке.
Среднее давление, действующее на плоскую фигуру, погруженную под слой жидкости, определяется из уравнения
где S — площадь фигуры.
Уравнение, позволяющее определить гидростатическое давление р в любой точке неподвижной жидкости в том случае, когда из числа массовых сил на нее действует лишь одна сила тяжести, называется основным уравнением гидростатики. Оно имеет вид:
p = p0 + hg ,
где р0 — поверхностное давление (рисунок 2), h — заглубление точки М под свободной поверхностью, g — удельный вес жидкости (для воды g = 10 4 Н/м 3 ).
Сила давления жидкости на плоскую фигуру определяется произведением площади Фигуры S на давление жидкости в ее центре тяжести рс:
2. ЭКСПЕРЕМЕНТАЛЬНАЯ УСТАНОВКА
Схема лабораторной установки показана на рисунке 3. Она состоит из следующих основных элементов: бака 10, с помещенным внутри клапаном 3. Клапан закрывает собой сливную трубу 2, в которой имеется запорный кран 1. Клапан закреплен на рычаге 8 и может открывать сливную трубу, поворачиваясь вокруг оси, проходящей через верхнюю часть стойки 9.
Поднятие клапана осуществляется путем навески грузов 4 на конец шнура 5, проходящего через блоки 6. Противоположный конец шнура присоединен к рычагу 8.
Для контроля уровня воды над клапаном на одной стороне бака установлена пьезометрическая трубка 7 с делениями.
С целью получения результатов достаточной точности в работе используются грузы с массой 0,5…0,02 кг.
Установки имеет следующие технические характеристики: L=18 см, l=12 см, a = 30°, dо = 5 см, Gкл = 5 Н.
3. ПРОВЕДЕНИЕ ОПЫТА И ОБРАБОТКА ОПЫТНЫХ ДАННЫХ
Теоретическое значение силы FТ, действующей на клапан определяется из выражения:
где hс — заглубление, центра тяжести крышки под свободной поверхностью (величина hс равна показанию уровня жидкости в открытом пьезометре), м; S0= — площадь отверстия, м 2 .
Рисунок 3 — Схема лабораторной установки
Использование в уравнении (1) площади отверстия определяется тем, что вне площади отверстия распределенные силы давления жидкости, действующие на верхнюю и нижнюю поверхности клапана, практически взаимно компенсируются.
В ходе проведения эксперимента к рычагу клапана постепенно прикладывается сила груза Gгр (рисунок 4). В том случае, когда момент силы Gгр относительно оси вращения (точка О) уравновесит противо- действующие ему моменты силы Fэ и веса клапана Gкл, клапан начнет открываться. При этом в момент открытая клапана будет выполняться равенство:
где l и L — длины плеч приложенных сил. Отсюда следует:
Формула (2) позволяет определить экспериментальное значение силы давления жидкости на клапан.
Работа проводится в следующей последовательности:
1) Наполнить бак 10 (см. рисунок 3) водой до уровня hс.
2) Открыть кран 1.
3) Навесить груз 4, постепенно увеличивая его вес до момента открытия клапана.
4) Записать величину груза и уровень hс в таблицу. При этом надо помнить, что вес груза, выраженный в ньютонах, определяется произведением массы груза, выраженной в килограммах, на ускорение свободного падения, т.е.
5) Снять разновесы.
Повторить опыт дважды при разном уровне воды hс (указывается преподавателем).
Теоретические значения силы давления жидкости, действующей на клапан, рассчитываются согласно уравнению (1), а ее экспериментальное значение по формуле (2). Погрешность опытных данных определяется по формуле
Полученные данные занести в таблицу.
Опытные данные и результаты опытов
Источник: vunivere.ru