1- золото2- платинаСколько литров золота содержится в награде?V1 = V-V2 = 20^3 — 10^3 = 7000 см3 = 0,007 м3 = 1 л V2 = 10^3 = 1000 см3 = 0,001 м3Сколько килограммов придется поднять чемпиону для того, чтобы получить награду?M = m1 +m2 = V1*p1 +V2*p2 = 0,007 м3 *19300 кг/м3 +0,001 м3 *21500 кг/м3 = 156,6 кг
Источник: znanija.site
Сколько золота содержится в графитовых рудах?
07 Ноя 2012

Сколько золота?
На сегодняшний день в России минимум, при котором месторождение имеет смысл разрабатывать, это 5 г/т. В графитовых рудах при химическом анализе обнаруживали 0,021—3,57 г/т золота, поэтому добывать из них золото считалось бессмысленным. Однако с помощью ионной масс-спектрометрии удалось обнаружить, что золота и платиноидов в графитовых рудах в разы больше. Так, в изученных пробах золота было до 17,8 г/т — это уровень богатых золотых приисков.
микрон 1 — золото в советской технике ✔ разбор на цветмет и драгметаллы
“Эта разница отражает существенные потери благородных металлов при термоокислительном разложении графитсодержащих проб в результате эмиссии летучих металлоорганических соединений”, — поясняет академик Александр Ханчук, руководитель группы, сделавшей открытие. Попросту говоря, во время химической реакции золото и другие благородные металлы испарялись из пробирки, давая неверные результаты.
Как любят говорить в передовицах газет, это открытие российских ученых трудно переоценить. И это действительно так.
Сообщество путешественников touroid.ru — это реальные отчеты и отзывы об отелях по всему миру.
Похожие статьи
- Извлечение золота из графитовых месторождений значительно повлияет на мировую экономику
- Где находятся графитовые месторождения, содержащие золото?
- Учеными открыты огромные залежи золота
- Виды золота в природе
Источник: pantikapei.ru
ОГЭ, Математика.
Геометрия: Задача №F26B00

Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника BKP к площади треугольника AMK.
Решение задачи:
BM — медиана треугольника АВС, следовательно, она делит этот треугольник на два равных по площади треугольника ( свойство медианы).
S ABM =S CMB =S ABC /2
Рассмотрим треугольник ABM.
S ABK +S AMK =S ABM =S ABC /2
AP — биссектриса, по теореме о биссектрисе можно записать AM/AB=KM/BK.
По условию задачи AC втрое больше AB, следовательно, AM в 1,5 раза больше АВ (т.к. является половиной АС)
Сколько золота в часах Au10.
KM/BK=1,5. Т.к. площадь треугольника вычисляется по формуле S=1/2*h*a, где а-основание и h-высота, то можем записать:
S AMK =1/2*h*KM=1/2*h*(1,5*BK),
S AMK =1/2*h*(3/2*BK)=3/2*(1/2*h*BK)=3/2*S ABK (т.к. высота h для этих треугольников общая)
S ABK =2/3*S AMK
S ABK +S AMK =S ABM =S ABC /2
2/3*S AMK +S AMK =S ABC /2
5/3*S AMK =S ABC /2
S AMK =0,3*S ABC
Как было найдено ранее, S ABK =2/3*S AMK
S ABK =2/3*0,3*S ABC
S ABK =0,2*S ABC
По тому же свойству биссектрисы для треугольника ABC получаем, что AC/AB=CP/PB
AC/AB=3 (по условию задачи), следовательно, CP=3*PB
S APC =1/2*h*PC=1/2*h*(3*PB)=3*(1/2*h*PB)=3*S ABP ,
S ABP +S APC =S ABC
S ABP +3*S ABP =S ABC
S ABP =S ABC /4
S BKP =S ABP -S ABK
S BKP =S ABC /4-0,2*S ABC =0,25*S ABC -0,2*S ABC =0,05*S ABC
Отношение S BKP к S AMK равно 0,05/0,3=5/30=1/6
Ответ: Отношение S BKP к S AMK равно 1/6.
Присоединяйтесь к нам.
Вы можете поблагодарить автора, написать свои претензии или предложения на странице ‘Про нас’
Другие задачи из этого раздела
Задача №00F003
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Задача №3B4B4B

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 136. Найдите стороны треугольника ABC.
Задача №FE0565
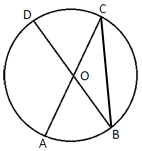
В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 128°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Задача №41017F
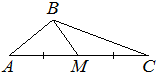
В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
Задача №0B70B9

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
Источник: otvet-gotov.ru
