К понятию о Золотом сечении / О. В. Максименко, В. С. Пастор, П. В. Ворфоломеева [и др.]. — Текст : непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 35-39. — URL: https://moluch.ru/young/archive/9/619/ (дата обращения: 11.07.2023).
«Геометрия владеет двумя сокровищами:
одно из них — теорема Пифагора,
другое — деление отрезка в среднем и крайнем отношении»
Золотое сечение – это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве — во всем, с чем может соприкоснуться человек. Авторы статьи исследуют литературу, находят связи между науками, касающиеся Золотого сечения, выявляют практический смысл золотых пропорций.
Ключевые слова: золотое сечение, золотые пропорции, научный феномен.
Целью нашей работы является исследование источников информации, касающихся «Золотого сечения» в различных областях знаний, выявление закономерностей и нахождение связей между науками, выявление практического смысла Золотого сечения.
Золотое Сечение наглядно — простой способ
Актуальность данного исследования определяется многовековой историей использования золотого сечения в математике и искусстве. То, над чем ломали голову древние, остается актуальным и вызывающим интерес современников.
Во все времена люди пытались находить закономерности в окружающем их мире. Окружали себя предметами «правильной» с их точки зрения формы. Лишь с развитием математики людям удалось измерить «золотое соотношение», которое впоследствии получило название «Золотое сечение».
Золотое сечение— гармоническая пропорция
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или, другими словами, меньший отрезок так относится к большему, как больший ко всему (Рис.1).

a:b = b:c
Рис. 1. Деление отрезка по золотым пропорциям
Напомним Вам, что же такое золотое сечение. Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина — 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62 % на 38 %. Это соотношение действует в формах пространства и времени [1].
Золотой треугольник ипрямоугольник
Кроме деления отрезка на неравные части (золотое сечение) рассматривают золотой треугольник и золотой прямоугольник [3].
Золотой прямоугольник — это прямоугольник, длины сторон которого находятся в золотой пропорции (Рис.2).
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения (Рис.3).
Золотое сечение в математике – математик Алексей Савватеев | Научпоп

Рис.2. Золотой прямоугольник

Рис.3 Золотой треугольник
Пентакль
В правильной пятиконечной звезде, каждый сегмент делится пересекающим его сегментом в золотом сечении, т. е. отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618 (Рис.4).

Пифагор утверждал, что пентаграмма, или, как он ее называл, гигиея представляет собой математическое совершенство, так как скрывает в себе золотое сечение. Отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому и есть золотая пропорция.
Ряд Фибоначчи
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих, а отношение смежных чисел ряда приближается к отношению золотого деления.
Так, 21: 34 = 0,617
34: 55 = 0,618.
История золотого сечения
Принято считать, что понятие о золотом делении ввёл в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н. э.). Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
Золотые пропорции вчастях тела человека
В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования».
Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон (Рис.5).

Рис.5 Золотые пропорции в частях тела человека
Золотое сечение вживой природе
Удивительно, как всего одно математическое понятие встречается во многих разделах человеческого знания. Оно как бы пронизывает все в мире, соединяя между собой гармонию и хаос, математику и искусство [2].
В биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.
В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции — длина ее хвоста так относится к длине остального тела, как 62 к 38 (Рис.6).

Рис.6 Золотые пропорции в частях тела ящерицы
Золотое сечение вархитектуре
В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. “Золотое сечение” дает наиболее спокойное соотношение размеров тех или иных длин.
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (Рис.7). Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.
Другим примером из архитектуры древности является пирамида Хеопса (Рис.8).
Пропорции Великой Пирамиды выдержаны в » Золотом соотношении»
Древние строители ухитрились возвести этот величественный монумент практически с идеальной инженерной точностью и симметричностью.

Рис.7. Парфенон

Рис.8. Пирамида Хеопса
Золотое сечение вскульптуре
Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям (Рис.9).

Рис.9 Статуя Аполлона Бельведерского
Золотое сечение вживописи
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Посмотрим внимательно на картину «Джоконда». Композиция портрета построена на золотых треугольниках (Рис.10).

Рис.10 Леонардо да Винчи «Джоконда»
Еще один пример золотого сечения в живописи – это полотно Рафаэля «Избиение младенцев» (Рис.11). На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается. золотая спираль!

Рис.11. Рафаэль «Избиение младенцев»
Золотое сечение влитературных произведениях
Формы временно̀го искусства по-своему демонстрируют нам принцип золотого деления. Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так, в повести «Пиковая дама» 853 строки, а кульминация приходится на 535 строке (853:535=1,6) — это и есть точка золотого сечения.
Золотое сечение вкинокартинах
Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей.
Заключение
О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Великий Пифагор создал тайную школу, где изучалась мистическая суть «золотого сечения». Евклид применил его, создавая свою геометрию, а Фидий — свои бессмертные скульптуры. Платон рассказывал, что Вселенная устроена согласно «золотому сечению».
А Аристотель нашел соответствие «золотого сечения» этическому закону. Высшую гармонию «золотого сечения» будут проповедовать Леонардо да Винчи и Микеланджело, ведь красота и «золотое сечение» — это одно и то же. А христианские мистики будут рисовать на стенах своих монастырей пентаграммы «золотого сечения», спасаясь от Дьявола.
При этом ученые — от Пачоли до Эйнштейна — будут искать, но так и не найдут его точного значения. Бесконечный ряд после запятой — 1,6180339887. Странная, загадочная, необъяснимая вещь: эта божественная пропорция мистическим образом сопутствует всему живому. Неживая природа не знает, что такое «золотое сечение».
Но вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Все живое и все красивое — все подчиняется божественному закону, имя которому — «золотое сечение». Так что же такое «золотое сечение»? Что это за идеальное, божественное сочетание? Может быть, это закон красоты?
Или все-таки он — мистическая тайна? Научный феномен или этический принцип? Ответ неизвестен до сих пор. Точнее — нет, известен. «Золотое сечение» — это и то, и другое, и третье. Только не по отдельности, а одновременно.
И в этом его подлинная загадка, его великая тайна.
- Виленкин Н. Я., Жохов В. И. и др. Математика — 6. — М.: Мнемозина, 2015
- Корбалан Ф. Золотое сечение. Математический язык красоты. (Мир математики Т.1). — М.: ДеАгостини, 2014
- Тимердинг Г. Е. Золотое сечение. — М.: Либроком, 2009
Основные термины (генерируются автоматически): золотое сечение, золотое деление, Золотой треугольник, золотая пропорция, золотой прямоугольник, деление отрезка, пропорция, научный феномен, синий отрезок, золотой.
Источник: moluch.ru
В чем золото метода золотого сечения
Вероятно, вы часто встречали упоминание о «правиле золотого сечения» и его важности для художника. Что же это за правило и как его применять, расскажет этот материал.
ЧТО ТАКОЕ ЗОЛОТОЕ СЕЧЕНИЕ
Золотое сечение — это пропорциональное соотношение двух величин.
В численном выражении это бесконечное число, которое округляют до 1,618 и обозначают число золотого сечения греческой буквой Ф (фи).
Если взять отрезок АВ и поделить его точкой С, то золотым сечением будет, когда меньший отрезок относится к большему так, как больший отрезок относится к целому.
Т.е. это пропорция, продолжающая саму себя.
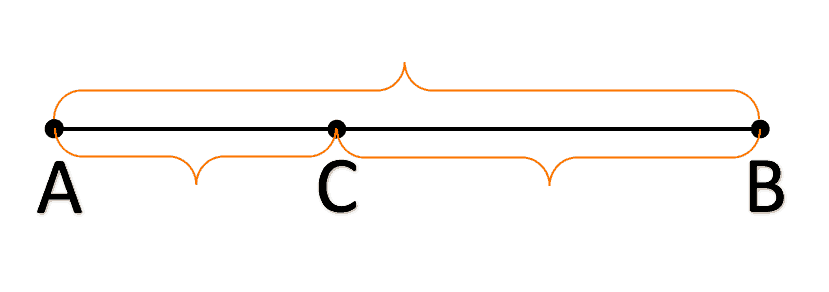
Если вы посмотрите на изображение ракушки, то увидите наглядный пример этого правила — каждое последующее деление меньше предыдущего в соотношении золотой пропорции:


Мифы о золотом сечении
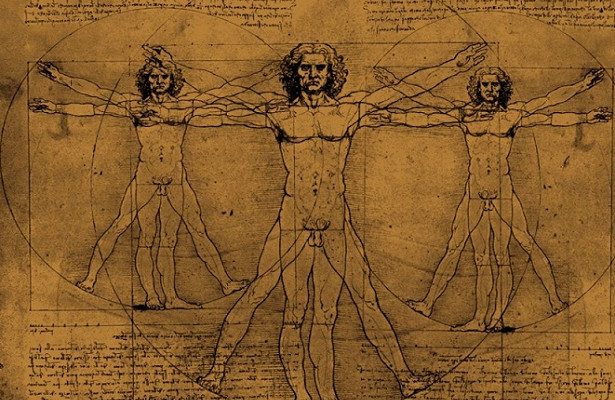
Идея золото сечения настолько красива, что стала очень популярной ещё сотни лет назад и остаётся такой до сих пор. За это время она обросла мифами, а люди попытались найти заветное золотое соотношение даже там, где его нет.
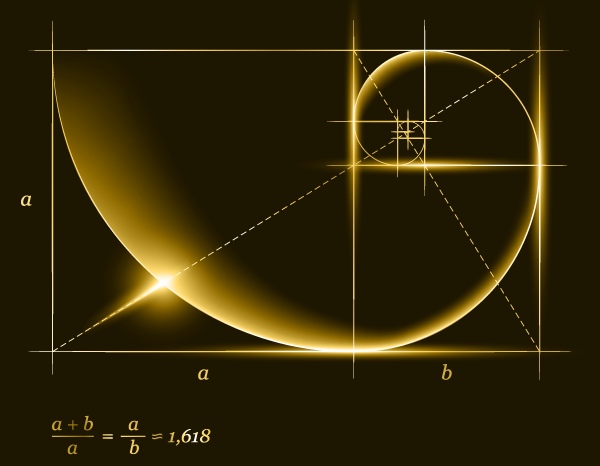
Это пересказ статьи Джорджа Марковски, PhD по математике из Гарварда. Решать, насколько эта информация авторитетна, вам
ММиф 1. Термин «Золотое сечение» использовался в античности
Многие считают, что знакомый нам сегодня термин был известен и в Античности, и у Леонардо да Винчи (одним из мифов является также то, что знаменитый художник и изобретатель использовал его в своих работах)

Но впервые термин в таком виде (разве что, на немецком) появился в 1835 году в книге Мартина Ома, брата знаменитого физика Георга Ома. На английском языке популярное сегодня название было впервые напечатано в 1875 году в Британской энциклопедии
Проблемы с измерениями
Часто золотое сечение находят в знаменитых памятниках архитектуры — Египетские пирамиды, Парфенон. Иногда авторы таких открытий рисуют золотые прямоугольники, игнорируя части объекта, не придерживаются какой-либо стандартной методологии или чистоты критериев. Неудивительно, что так им удаётся обнаружить искомое соотношение
Измерения реальных объектов всегда могут быть только приближениями. Но, если допустимая ошибка в измерениях составит ±1%, то ошибка соотношения будет составлять уже ±2%! Для инженеров-строителей рекомендовано придерживаться интервала ±0,2%, но в оригинальной статье автор принимает допустимой ошибку измерения ±1%, то есть интервал [1,58; 1,66] для золотого соотношения φ
Но одно лишь попадание соотношения сторон в этот интервал не значит, что φ запланировано внесено в конструкцию. Это лишь первый тест, означающий, что имеет смысл исследовать ситуацию дальше
ММиф 2. Великие пирамиды разработаны так, чтобы соответствовать φ
Многие люди находили φ в Великой пирамиде Хеопса, построенной за 2500 лет до нашей эры. Согласно одному из источников, длины сторон основания пирамиды варьируются от 755,43 футов до 756,08 футов, так что оно не является идеальным квадратом. Средняя длина — 755,79 футов. Высота указана равной 481,4 фута
Некоторые авторы утверждают, что Великая пирамида спроектирована так, что высота наклонной стороны относится к половине длины основания, как φ. По теореме Пифагора находим неизвестную сторону — она равна 612,01 футов

Это отношение действительно отличается от φ всего на 0,1%! Значит, имеет смысл провести более глубокое исследование
Гипотеза о нахождении φ в Пирамиде подтверждается словами древнегреческого историка Геродота. По его словам египетские жрецы сообщили ему, что размеры Великой пирамиды были подобраны так, что площадь квадрата, сторона которого была равна высоте пирамиды, равнялась площади треугольника стороны
Из этого утверждения выводится уравнение, решением которого действительно является φ. Проблема с опорой на утверждения Геродота в массе явных ошибок по отношению к описанию пирамид. Так, он указывает, что высота пирамиды, как и сторона квадрата в основании равнялась 800 футам. Но это не соответствует действительности ни сейчас, ни в прошлом. Также стоит заметить, что Геродот описывал Пирамиду через 2 тысячелетия после того, как она была построена

Таким образом, эта гипотеза имеет мало смысла. Непонятно также, почему Египтяне хотели бы построить пирамиду именно таким образом, и неизвестно, знали ли они число φ — оно почти не встречается в других их строениях
ММиф 3. Греки использовали φ в Парфеноне
Парфенон был построен в 5 веке до нашей эры. Многие прикладывают золотой прямоугольник к его фасаду, утверждая, что он идеально подходит. Однако, этих людей почему-то не смущает, что части здания выходят за пределы прямоугольника!

Измерения Парфенона значительно отличаются у разных авторов, потому что каждый проводит их из разных точек. С таким широким разбросом данных энтузиаст может выбрать, какие удобно ему для получения лучшего результата.
Например, одни авторы определяют высоту здания равной 45 футам и 1 дюйму, ширину — 101 футу, длину — 228 футам и 1/8 дюйма. Точки, между которыми проводились измерения не указываются. Но даже при этом отношение ширина/высота = 2,25 = 9/4, и длина/ширина = 2,25 — далеко за пределами допустимого интервала для φ. Можно предположить, что пропорции здания попросту отмерены в соотношении 4:9. Но другой автор приводит высоту, равной 59 футам. Тогда отношение ширины к высоте равно 1,71, что также не совпадает с золотым сечением.
Многие стремятся окутать мистицизмом древние строения, найти в них такие константы, как φ или π. Иногда такие случаи действительно встречаются, но это не значит, что мы можем обобщить их для всех знаменитых памятников. Слишком легко переоценить важность случайных отношений, которые, к тому же, могут быть неверно измерены
Это лишь часть перевода оригинальной статьи.
Источник: un-sci.com



