Что это? Золотое сечение – это математическая формула, соотношение двух неравных чисел. Его еще называют божественной пропорцией. Правило третей, золотая спираль – всё это визуальное отображения этого универсального правила.
Где используется? Золотое сечение применимо везде, где есть место графике, рисунку, фотографии. Сфера дизайна – не исключение. Конечно, это не единственное правило гармонии, но, пожалуй, самое известное.
- Что такое золотое сечение
- История золотого сечения
- Золотое сечение Фибоначчи
- Золотое сечение в природе
- Золотое сечение в фотографии
- Золотое сечение в дизайне
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.
Бесплатно от Geekbrains
Что такое золотое сечение
Это отношение двух разных по величине чисел, когда большее из них относится к меньшему так же, как и общая их сумма относится к большему. Соотношение золотого сечения равняется около 1,618. Его обозначают греческой литерой Ф (читается как «фи») в честь древнегреческого скульптора Фидия, который применял эти пропорции при создании храма Парфенон.
Принцип «Золотого сечения» — А. Рыжкин
Одним из популярных способов представления золотого сечения является прямоугольник с соотношением сторон 62 на 48 и построенной внутри спиралью.
История золотого сечения
Согласно истории, данное понятие для научного использования ввел Пифагор, философ и математик Древней Греции. Предполагается, что ученый позаимствовал знание у жителей Египта и Вавилонии.
Если посмотреть на соотношение сторон пирамид, храмов и предметов домашнего обихода у древних египтян, а также на украшения из саркофага царя Тутанхамона, то очевидно, что все они создавались по принципу золотого сечения.
Архитектор из Франции Ле Корбюзье заметил, что рельеф храма египетского правителя Сети I, как и в рельефе изображения царя Рамзеса, тоже создавались по этому правилу. Соотношения золотого деления были обнаружены и в рельефе гробницы, на котором изображен высокопоставленный чиновник Хесира.
Для вас подарок! В свободном доступе до 16.07 —>
Скачайте ТОП-10 нейросетей, которые помогут облегчить
вашу работу
Чтобы получить подарок, заполните информацию в открывшемся окне
Жители Древней Греции хорошо владели геометрией. Арифметике, например, они учились по геометрическим фигурам уже в детстве. А квадрат Пифагора и его диагональ служили основой для создания динамических прямоугольников.
Сам термин «золотое сечение» впервые ввел в обиход математик из Германской империи Мартин Ом в 19 веке. До того времени правило имело название «божественная пропорция».
Из-за уникальных свойств она пользовалась большой популярностью. Например, в эпоху Возрождения число 1,618 было идеальным при выборе размера. Его часто применяли для создания картин и книг. А линия талии в то время считалась границей золотого сечения в теле человека.
Многие люди и сегодня уверены, что соблюдение данного правила считается залогом красоты и внешней гармонии. Эту тему активно обсуждают пластические хирурги.
О ЗОЛОТОМ СЕЧЕНИИ И ПОЧЕМУ ОНО НАЗЫВАЕТСЯ ЗОЛОТЫМ #золотоесечение
Золотое сечение Фибоначчи
В конце 12 века математик из Италии Леонардо Пизанский, известный по прозвищу Фибоначчи, открыл последовательность чисел, связанных с золотой пропорцией. Суть в том, что если взять любые 2 числа из ряда итальянского математика, то соотношение между ними почти такое же, как на примерах золотого сечения. Особенность последовательности Фибоначчи в том, что каждое новое число всегда равняется сумме 2-х предыдущих. Пример: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д.
По мере увеличения ряда, отношения между числами становится все ближе к 1,618. Разделив, к примеру, 8 на 5, мы получим около 1,6. А соотношение 34 на 21 уже дает 1,619, если округлить. Каждое число ряда является логичным в последовательности Фибоначчи.
Такие соотношения из-за приближения к показателю золотого деления можно использовать при построении золотого прямоугольника. Эта фигура считается одной из самых гармоничных в геометрии, что позволяет применять пропорции Пифагора в любом виде изобразительного искусства.
Золотой прямоугольник тесно связан с золотой спиралью, которая строится методом размещения смежных между собой квадратов по алгоритму Фибоначчи.
Золотое сечение в природе
Пропорции золотого сечения можно наблюдать во всех природных и научных проявлениях. В представленном списке мы рассмотрим наиболее удивительные случаи.
- Лепестки у цветов. Нередки случаи, когда их количество соответствует числовому ряду «Ф». По мнению Дарвина, все лепестки растений располагаются так, чтобы получать как можно больше солнечного света и остальных необходимых для жизни ресурсов.
- Головки у семян. Во многих случаях семена цветов начинают расти посередине головки семени и появляются снаружи, заполняя собой пространство. В качестве примера можно привести семена подсолнуха.
- Шишки у сосен. Семена, находящиеся в их семенных коробочках, произрастают вверх противоположно друг другу по спирали. Расстояние между ними обычно совпадает с соотношениями чисел из последовательности Фибоначчи.
- Ветки у деревьев. На примере их формирования и расщепления также можно заметить правило золотого ряда. То же самое относится и к развитию корневых систем у растений и водорослей.
- Раковины. Большинство из них демонстрируют нам правило золотого сечения. Например, это можно сказать об улитках и наутилусах.
- Спиральные галактики. Млечный Путь содержит в себе несколько рукавов, представленных в виде изогональных спиралей с шагом около 12 градусов. Их форма соответствует форме золотой спирали, при том над каждой такой галактикой можно начертить золотой прямоугольник.
- Ураганы. В большинстве случаев, изнутри они устроены согласно последовательности ряда «фи».
- Пальцы на руках у людей. Все участки пальцев от начала основания и до запястья увеличивается в соотношении по Фибоначчи.
- Тела людей и животных. Расстояние у людей от пупка до пола, а также от темени и до пупка — это яркий пример закона золотого сечения. Помимо человека такую пропорцию можно наблюдать и у других организмов (например, у дельфинов и пчел).
- Молекулы ДНК. Все они содержат соотношение 34 на 21 ангстрем в каждом полном спиральном цикле. А вы уже знаете, что эти цифры — часть ряда Фибоначчи.
Узнай, какие ИТ — профессии
входят в ТОП-30 с доходом
от 210 000 ₽/мес
Команда GeekBrains совместно с международными специалистами по развитию карьеры подготовили материалы, которые помогут вам начать путь к профессии мечты.
Подборка содержит только самые востребованные и высокооплачиваемые специальности и направления в IT-сфере. 86% наших учеников с помощью данных материалов определились с карьерной целью на ближайшее будущее!
Скачивайте и используйте уже сегодня:

Александр Сагун
Исполнительный директор Geekbrains
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Получить подборку бесплатно
Уже скачали 21635
Как мы видим, примеров, где можно увидеть пропорции и соотношения по принципу золотого правила, довольно много. Помимо случаев, описанных выше, 1,618 постоянно встречается в точных науках, биологии и других областях жизни. Поэтому свое альтернативное название — божественное сечение, правило полностью оправдывает. Ведь материальный мир словно был создан по этому закону.
Золотое сечение в фотографии
Гармоническая пропорция напрямую связана с правилом третей — другой неотъемлемой схемой для работы с визуалом. По сути, оно продолжает золотое сечение так же, как, например, фотография рождается из художественного творчества.
Основное различие заключается в соотношении сторон. Так, в принципе третей кадр разделяется на 3 одинаковые части, а в божественной пропорции он делится на 1:0.618:1.
Отсюда следует, что правило третей можно назвать более простой версией золотого сечения, но полностью рабочей.
Например, сегодня большинство камер, в том числе и в смартфонах, имеет разлинованную сетку третей, что позволяет пользователям гармонично выстраивать композицию из фото и видео.
Чем следует руководствоваться при съемке?
- Точки пересечения. Благодаря размещению нужного объекта по линиям, сделать снимок будет намного удобнее.
- Диагональная композиция. Линию можно прочертить самостоятельно из верхнего угла кадра в нижний, а можно использовать объекты, находящиеся в этой последовательности, которые формируют эту линию. Наличие разных диагоналей позволяет получить динамичный кадр. Восходящая, например, из правого нижнего угла в левый верхний придаст фотографии веселое настроение, а нисходящая — грустное.
- Пропорции. Чаще всего это относится к взаимосвязи объектов на нескольких планах снимка. Это тоже вариант золотого сечения, только представленный в соотношении объектов. Например, на заднем плане к большему объекту на переднем плане (либо наоборот).
- Линия горизонта. Когда вы делаете снимок на природе либо в городской инфраструктуре, нужно расположить горизонтальную линию кадра на одной из горизонтальных линий третей. То же самое относится и к общему плану фотографии/видео. Это даст более качественный результат.
- Правило «воздуха». Не забывайте про свободные участки между объектами. Если вы делаете фотографию человека, то оставьте немного пространства от его головы до границы кадра. А в ситуации, когда он смотрит налево, разместите человека по правым точкам пересечения линий (верно и обратное).
Золотое сечение в дизайне
Божественная пропорция делает современный дизайн более упорядоченным. Легкий и быстрый способ использования этого — умножить размер одного элемента на 1,618. Результат покажет, каким должен быть размер следующего объекта.
Применение формулы золотого сечения в типографике
Определяющими факторами в данной области являются 3 составляющие: размер шрифта, ширина линии и высота строки. Их необходимо подбирать в правильных пропорциях.
Увеличивая и уменьшая шрифт, а также ширину текста, можно определить, какую высоту следует задать буквам. Установлено, что оптимальным для удобства читателей количеством является 70-80 символов на строку. Когда длина текста превышает этот показатель, его читабельность сильно снижается.
Для примера возьмем текст из 3 строк и определим в нем 3 части: «А», «Б» и «В». Допустим, строка «В» содержит меньше ценной информации, чем «А» и «Б». В связи с этим, текст внутри строки «В» должен иметь шрифт размером 10. Чтобы установить размер контента на строке «Б» (второй по значимости контента), надо умножить 10 на 1,618.
В разработке логотипов
Большинство популярных брендов, например, «Твиттер», «Эппл» и «Пепси», применяют знания божественного сечения, когда создают фирменный логотип.
Поэтому вы тоже можете пользоваться правилом чисел «Ф» при создании сетки. Полученный результат станет вашей опорой в разработке графического рисунка.
Золотое сечение в архитектуре
Зодчие прошлого применяли принцип божественного деления при создании памятников. Мавзолей-мечеть Тадж-Махал, например, относится к одному из 7 чудес света. Когда его возводили, мастера пользовались правилом золотого сечения.
Применение этого знания в современной архитектуре дает возможность добиться баланса между шириной и высотой сооружения. Популярным методом построить гармоничное здание является использование свойств золотого прямоугольника.
Стоит добавить, что золотое сечение дает возможность творить разнообразные формы. При их создании нет необходимости строго следовать прямоугольной структуре. Золотое деление позволяет дизайнерам применять полученные формы как основу для работы.
Разработка проектов и формирование макетов
Чтобы сделать макеты качественными, нужно учесть 2 главные составляющие: отдельные визуальные элементы и как они будут связаны между собой.
Есть много способов формирования макетов. Например — расположение «Z». Оно дает увидеть путь, по которому проходит посетитель на веб странице, а также схему того, как он смотрит на элементы.
Источник: gb.ru
Золотое сечение, золотая пропорция, число Фибоначчи простым языком и как это применять в дизайне

Золотое сечение или золотая пропорция известна тысячи лет, её применяли ещё в Античной Греции. Это природная закономерность, природная пропорция, можно называть как угодно, но она встречается в природе и окружает нас. Она для нас очень привычна, хотя мы это и не отслеживаем, но наш мозг считывает её как паттерн и воспринимает как что-то хорошее и красивое.
Золотая пропорция — это пропорция асимметрии, но соотношение частей такое, что создает гармонию и выглядит эстетично, что подразумевает для нас «выглядит привычно», «выглядит естественно». Золотая пропорция имеет идеальное соотношение частей, когда отношение меньшей части к большей такое же, как большей части к целому. Это динамическая симметрия и она характерна для роста живой материи.
Я уже писала о золотой пропорции в статье про восприятия человеком красоты, и приводила исследования генетиков и там же рассказывала о том, что все красивые лица на взгляд человека вписываются в пропорцию золотого сечения. Эта тема будоражила деятелей творчества очень много веков. Архитекторы, скульпторы и художники пытались внедрить в свои творения эти пропорции, чтоб достичь красоты. Сегодня происходит все то же самое, и дизайнеры создают свои продукты с учетом этой пропорции.
Давайте разбираться, что такое Золотое сечение
Если опустить всю сложную терминологию и упростить до процентных соотношений, то золотая пропорция будет такой: 100%=62%+38%
Проще говоря, золотая пропорция это деление объекта на две неравные части, где одна часть занимает 62% от целого, а вторая часть занимает 38% от целого.
И получается, что 62% относится к 100%, точно так же как 38% относится к 62%. Отсюда любой объект можно делить бесконечно.

Пример 1. Всё что угодно, целое, мы берём за 100%. Например, формат A4, т.е. вся его площадь это у нас 100%. Чтоб его поделить пополам по золотому сечению мы делим на неравные части, где одна часть занимает 62%, а другая 38%. Все.
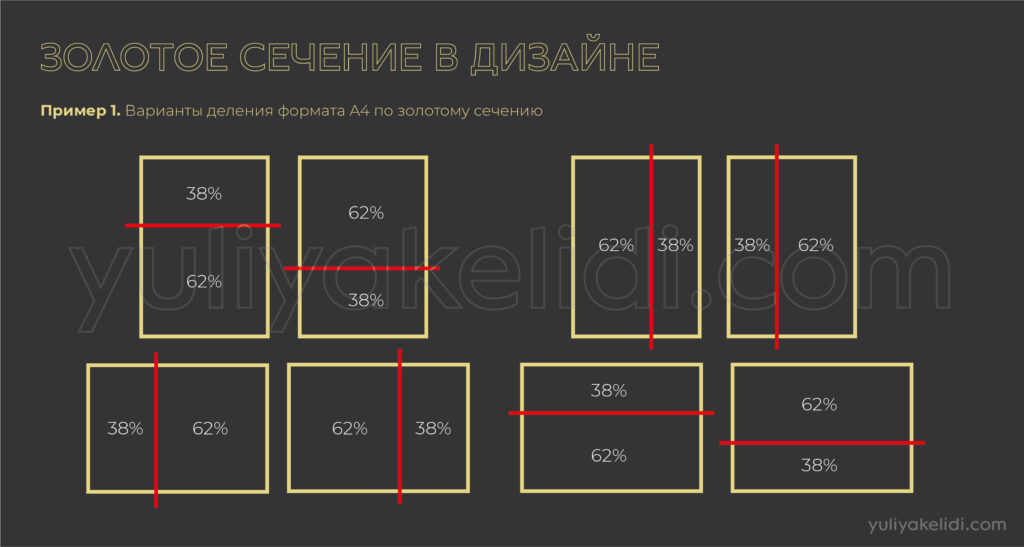
Пример 2. У нас есть дорога. Она длиной 2000 м. её надо поделить по золотому сечению. Мы находим, сколько будет 62% от 2000 м. Получается 1240 м. Мы делим нашу дорогу 2000 м. на отметке в 1240 м. И получим деление прямой по золотой пропорции. Все.

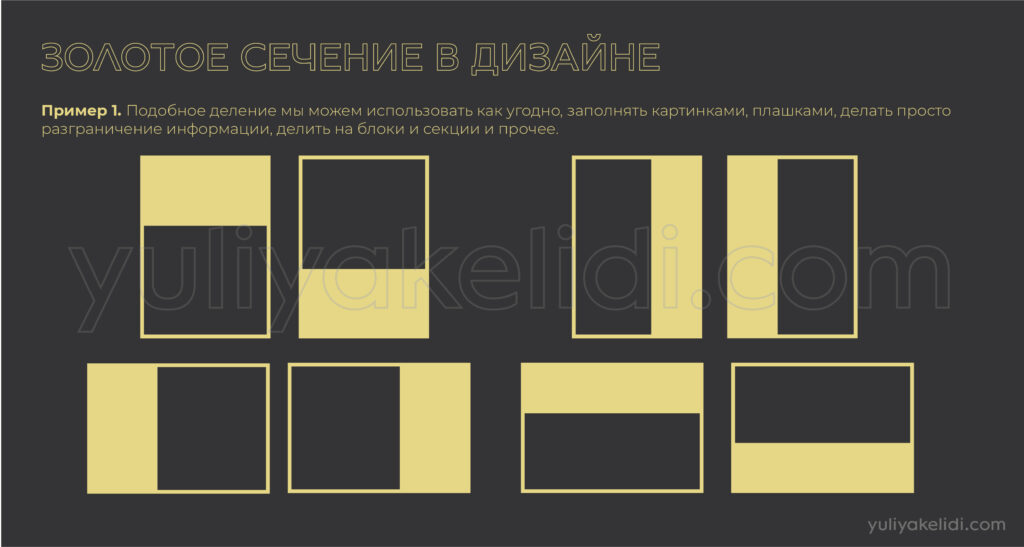
Пример 3. Нам надо чтоб общий объем объектов был расположен к целому по золотой пропорции. Например, в плакате мы хотим, чтоб информация была распределена по золотому сечению.
Шаг 1. Формат плаката это наши 100%. Весь текст и картинки мы собираем вместе и они должны занять площадь на плакате в 62%. Остальное будет воздухом.
Шаг 2. Мы в этом объеме 62% подбираем оптимальные размеры для каждого объекта и потом распределяем по плакату.
Итого: наши объекты суммарно займут 62% площади плаката, а 38% площади плаката останется в качестве свободного пространства, т.е. воздуха. Все.

Пример 4. Нам нужно задать ритмический ряд, который будет уменьшаться в золотой пропорции. У нас есть условный объект. Его изначально мы задаем в размерах, допустим 50 мм, которые обозначаем как 100%. Следующая копия этого объекта должна быть 62%, т.е. от 50 мм. мы находим 62%. Это будет 31 мм.
Далее, чтоб найти размер следующего объекта, мы берем 31 мм как 100% и от него находим 62%. Получается 19,22. Следующий будет 11,9 мм. Все.

Пример 5. Например, используя золотое сечение, мы можем найти идеальные значения кегля шрифта. Самый крупный текстовый блок у нас идёт 120 pt, чтоб найти размер кегля для меньшего текста, но с золотой пропорцией, мы задаём его в размере 62% от 120. Получаем 74 pt, следующий блок мы уже ищем 62% от 74. Получаем 46 pt. Это и будет уменьшение кегля текста с учетом золотого сечения.

Вариантов применения очень и очень много!
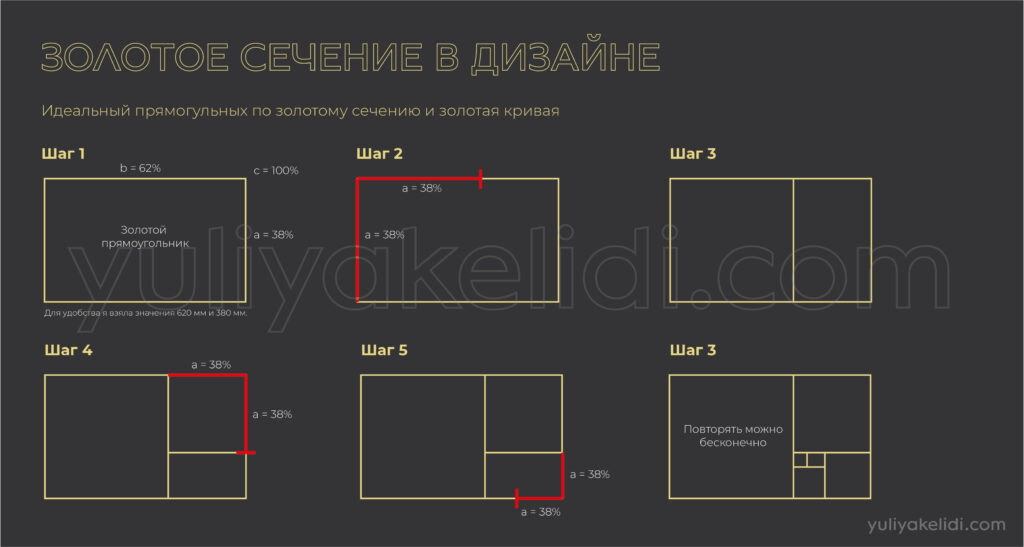
Идеальный прямоугольник по золотому сечению
Чтоб получить знаменитый золотой прямоугольник, по которому потом строится самая знаменитая кривая, нам надо также построить его в пропорциях 62%-38%.
Одна сторона прямоугольника будет равна 62%, а вторая 38%. В сумме они дают 100%. Получается та самая, знаменитая формула, которую записывают в обозначениях a,b,c.
Как звучит определение золотого сечения:
Золотая пропорция — соотношение двух величин, при котором большая величина относится к меньшей, так же, как сумма величин к большей. И далее невероятно сложное объяснение с кучей формул. Давайте упрощать и разбираться, что это все значит. Потому что дизайнеру, для работы, все эти формулы не нужны.
100% — это с,
38% — это а,
62% — это b
Золотая пропорция гласит, что a:b = b:c. В цифрах мы получаем следующее: 38:62 равняется 62:100. Да, действительно, если мы поделим 38 на 62, то получим 0,62, и если мы 62 поделим на 100, то получим также 0,62.
Золотая пропорция продолжается и гласит, что c:b = b:a. Давайте снова в цифрах: 100:62 и 62:38. И в одном и во втором случае мы получаем 1,61.
Вот цифра 1,61 это число Фибоначчи, это число золотой пропорции, число золотого сечения, называйте, как хотите, это одно и то же. По-гречески называют «фи» —φ. Его округляют до 1,62. Что в целом и означает 62% от 100%.
И получается пропорция, которую записывают как соотношение 62%-38%!

У золотого прямоугольника короткая сторона а — 38%, а длинная b — 62%. Для удобства, давайте и зададим числа 38 мм и 62 мм. Получим золотой прямоугольник.
Сторону b мы берем как 100 и делим её на 62% и 38%. К слову 62% от стороны b будут равняться 38 мм, т.е. стороне а. Таким образом мы получаем квадрат.
Дальше каждую сторону мы делим на пропорцию 62 и 38 и наш прямоугольник будет уменьшаться до бесконечности.
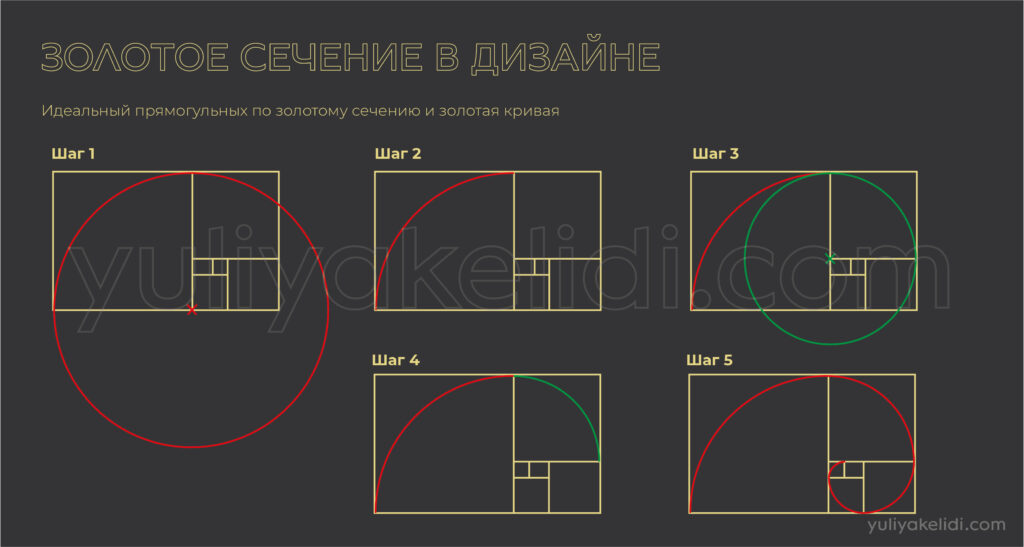
В получившиеся квадраты мы вписываем окружность. И соединяясь, она рисует нам природную кривую, которая характерна для живой материи.
В 2023 году я решила создать youtube-канал, на котором буду размещать обучающие ролики по графическому дизайну, также будут ролики про искусство.
Начала я записывать с уроков по изучению программы Adobe Illustrator.
Если вам интересно то, что я делаю, вы можете поддержать меня. Вот ссылка на канал, подпишитесь, пожалуйста.
Также мне важна любая обратная связь, чтоб создавать материалы ещё качественнее.
Теперь у меня появилась страница на Facebook. Если вам интересна эта тема, можете присоединиться и следить за выходом новых статей. Буду рада вас видеть
Источник: yuliyakelidi.com
Золотое сечение
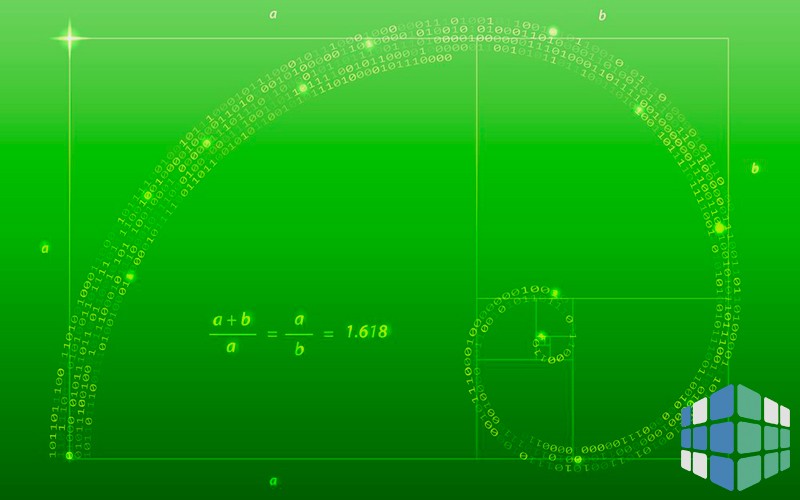
Золотым сечением называют число, полученное путем деления линии на две части таким образом, что более длинная часть (а), разделенная на меньшую часть (b), равна полной длине линии (а+b), разделенной на более длинную часть (а). Такое отношение часто символизируют с помощью литеры Ф (читается как «фи») – 21-й буквы греческого алфавита. В форме уравнения это выглядит так:
a / b = (a + b) / a = 1.6180339887498948420…
Как и в случае с π (пи, отношение длины окружности к ее диаметру), число Ф является бесконечным. Обычно его округляют до значения 1,618.
История открытия золотой середины
Это число было найдено и открыто много раз, поэтому у него так много разных названий — золотая середина, золотое сечение, божественная пропорция и т.д. Исторически его можно увидеть в архитектуре многих древних творений, таких как Великие Пирамиды и Парфенон. В пирамиде Гизы длина каждой стороны основания составляет 230,5 метров при высоте 146,6 метров. Отношение основания к высоте составляет примерно 1,5717, что близко к золотой пропорции.
Фидий (500 г. до н.э. — 432 г. до н.э.) был греческим скульптором и математиком, который, как считается, применил Ф, создавая скульптуры для Парфенона. Платон (428 г. до н.э. — 347 г. до н.э.) считал, что золотое сечение является наиболее универсальным связующим звеном математических отношений. Позднее Евклид (365 г. до н.э. — 300 г. до н.э.) связал золотое сечение с построением пентаграммы.
Последовательность Фибоначчи и золотое сечение
Около 1200 года математик Леонардо Фибоначчи открыл уникальные свойства последовательности Фибоначчи. Эта последовательность непосредственно связана с золотым сечением, потому что если взять любые два последовательных числа Фибоначчи, их отношение будет очень близко к золотому сечению. По мере того как числа возрастают, соотношение приближается к значению 1,618.
Например, соотношение 3 к 5 составляет 1,666. Но соотношение 13 к 21 составляет 1,625. Возрастая, соотношение 144 к 233 составляет 1,618. Все эти числа являются последовательными числами в последовательности Фибоначчи.
Такие соотношения из ряда Фибоначчи, близкие к значению золотого сечения, могут быть применены к пропорциям прямоугольника, называемого золотым прямоугольником. Он известен как одна из наиболее визуально совершенных из всех геометрических форм — следовательно, правило золотого сечения очень широко применяется во всех видах визуального искусства. Золотой прямоугольник также связан с золотой спиралью, которая создается путем создания смежных квадратов измерений Фибоначчи.
Пропорции золотого сечения в материальном мире
В 1509 году Лука Пачоли написал книгу, которая называет число Ф «Божественной пропорцией», что было наглядно показано Леонардо да Винчи. Позже да Винчи назвал эту пропорцию золотым сечением. Оно использовалось для достижения баланса и красоты во многих картинах и скульптурах эпохи Возрождения.
Да Винчи сам использовал золотое сечение, чтобы определить все пропорции в «Тайной вечере», включая размеры стола, пропорции стен и деталей интерьера. Золотое сечение также появляется в «Витрувианском Человеке» да Винчи и «Мона Лизе». Считается, что золотое сечение использовали и другие великие художники, включая Микеланджело, Рафаэля, Рембрандта, Сьюрата и Сальвадора Дали.
Термин «фи» был придуман американским математиком Марком Барром в 1900-х годах. Ф продолжал применяться в математике и физике, в том числе в плитках Пенроуза 1970-х годов, которые позволяли мозаичным поверхностям иметь пятикратную симметрию. В 1980-х годах Ф появился в квазикристаллах – недавно открывшейся форме материи.
Фи — более чем загадочный и неясный термин в математике и физике. Он появляется вокруг нас в нашей повседневной жизни, даже в наших эстетических взглядах. Исследования показали, что когда испытуемые видят случайные лица, они считают наиболее привлекательными те, которые имеют четкие параллели с золотым сечением. Лица, оцененные как наиболее привлекательные, показывают золотые соотношения между шириной лица и шириной глаз, носа и бровей. Испытуемые не были математиками или физиками, знакомыми с правилом золотого сечения (они были просто среднестатистическими людьми), и оно вызвало инстинктивную реакцию.
Золотое сечение также проявляется во всех видах природы и науки. Ниже приведены примеры самых неожиданных мест, в которых можно его встретить.
- Цветочные лепестки. Количество лепестков на некоторых цветах соответствует последовательности Фибоначчи. С точки зрения теории Дарвина считается, что каждый лепесток помещается таким образом, чтобы обеспечить максимально возможное воздействие солнечного света и других факторов.
- Семенные головки. Семена цветка часто начинают произрастать в центре семенной головки и мигрируют наружу, заполняя свободное пространство. Например, семечки подсолнухов следуют этой схеме.
- Сосновые шишки. Семенные коробочки сосновых шишек наполнены семенами, которые растут спирально вверх, в противоположных направлениях. Количество шагов, которые делают спирали, как правило, соответствует числам Фибоначчи.
- Ветви дерева. То, как ветки дерева формируются или расщепляются, является примером последовательности Фибоначчи. Корневые системы и водоросли также придерживаются такого способа формирования.
- Раковины. Многие раковины, в том числе раковины улитки и раковины наутилуса, являются прекрасными примерами золотой спирали.
- Спиральные галактики. Млечный путь имеет несколько спиральных рукавов, каждый из которых имеет логарифмическую спираль примерно 12 градусов. Форма спирали идентична золотой спирали, а золотой прямоугольник можно нарисовать над любой спиральной галактикой.
- Ураганы. Внутреннее строение ураганов часто следует правилу золотой спирали.
- Пальцы руки человека. Каждый участок пальца от кончика основания до запястья больше, чем предыдущий, примерно на соотношение Ф.
- Тела человека и животных. Расстояние от пупка человека до пола и от макушки головы до пупка – это золотое сечение. Но человек не единственный пример золотого сечения в животном мире. Дельфины, морские звезды, морские ежи, муравьи и пчелы также демонстрируют эту пропорцию.
- Молекулы ДНК. Молекула ДНК имеет размеры 34 ангстрем на 21 ангстрем на каждом полном цикле спирали в виде сдвоенной спирали. В рядах Фибоначчи 34 и 21 являются последовательными числами.
Таким образом, примеров, где встречаются пропорции и соотношения, следующие правилу золотого сечения, более чем достаточно. Кроме перечисленных примеров, число «Фи» часто встречается в математике, физике, астрономии, биологии и иных сферах деятельности человека. Можно смело утверждать, что название «Божественное сечение» по праву присвоено числу Ф – видимо им руководствовался создатель, наполняя эту Вселенную всем живым и неживым.
Советуем также прочитать:
Источник: 4brain.ru