Что значит касательные украшения

касательной, ж. (мат.). Прямая линия, имеющая одну общую точку с кривой. Провести касательную к кругу.

Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.

касательная

ж. Прямая линия, имеющая с кривой одну общую точку, но не пересекающая ее (в математике).

Энциклопедический словарь, 1998 г.

касательная

КАСАТЕЛЬНАЯ прямая к кривой L в точке M предельное положение (на рисунке MT), к которому стремится секущая ММ? при приближении точки М? к точке М.

Имена, названия, словосочетания и фразы содержащие «касательная»:

Большая Советская Энциклопедия

Касательная

к кривой линии, предельное положение секущей. К. определяется так. Пусть М ≈ точка кривой L (рис. 1). Выберем на L вторую точку M» и проведём прямую MM».

Будем считать М неподвижной, а точку M» приближать к М по кривой L. Если при неограниченном приближении M» к М прямая MM» стремится к одному определённому положению MT, то MT называется касательной к кривой L в точке М. Не у всякой непрерывной кривой имеются К., поскольку прямая MM» может не стремиться к предельному положению или может стремиться к двум разным предельным положениям, когда M» стремится к М с разных сторон от М (рис. 2). Встречающиеся в элементарной геометрии кривые имеют вполне определённую К. во всех точках, кроме некоторого числа «особых» точек. Если кривая на плоскости в прямоугольных координатах определяется уравнением у = f (x) и f (х) дифференцируема в точке x0, то угловой коэффициент К. в точке М с абсциссой x0 равен значению производной f»(x0) в точке x0, уравнение К. в этой точке имеет вид:

Окружность, касательная, секущая и хорда | Математика

у ≈ f (x0) = f «(х0)(х ≈ x0).

Касательной (прямой) к поверхности S в точке М называют любую прямую, проходящую через точку М и лежащую в касательной плоскости к S в точке М.

Имена, названия, словосочетания и фразы содержащие «касательная»:

Примеры употребления слова касательная в литературе.

Трое мужчин, которые в этом смысле составляли личную проблему Касательной, назывались Кварк, Ангстрем 3754 и Ищи-и-Скажи.

Они вышли к нашему барражу по касательной, перестроились из клина в такой же точно диск, как наш, и тоже закружились.

Вечно бдящий Старший Братец усечет и пришлет нам касательную, что указанная Крисса Джейн Тулл состоит в экспедиции и название отвергается, а так как на этот раз они сумеют установить связь, нас заштрафуют до полусмерти.

Третий выстрел прошел по касательной, задев правую щеку Генри Бофорта и взметнув кучу кровавых брызг и распоротой плоти.

Видите ли, согласно моим расчетам, положение этой нитки в пространстве в каждый момент времени представляет собой вектор, коллинеарный касательной к кривой перемещения моего центра массы по коридору отделения 1Б.

Ерунда, скользнуло по касательной, но я на минуту лишился сознания, и за это время Линд оторвался от погони.

Они отправили экспедицию под руководством удивительной женщины хичи по имени Касательная, и им стала ясна вся кошмарная картина.

Что такое касательная | Осторожно, спойлер! | Борис Трушин |

Когда я сказал, что Касательная была исследователем, я совсем не имел в виду, что она отправлялась на поиски географических знаний, как Магеллан или капитан Кук.

Мне Касательная показалась бы кошмаром из моего детства на пищевых шахтах в Вайоминге.

Будучи женщиной, Касательная была лысой — у мужчин иногда бывает пушок на черепах, у женщин никогда.

Это делает еще более болезненным тот факт, что Касательная сыграла решающую роль в падении хичи.

В своем историческом полете Касательная командовала большим кораблем хичи.

К несчастью для тебя, — выпалила Касательная, но тут же взяла себя в руки.

Через двадцать дней после прибытия на орбиту вокруг планеты лежебок Касательная была готова к работе.

А существенно то, что Касательная со своим экипажем сделала то, что почти никогда не делают корабли хичи.

Источник: библиотека Максима Мошкова

Дополнительная информация:

Транслитерация: kasatel’naya
Задом наперед читается как: яаньлетасак
Касательная состоит из 11 букв

Источник: xn--b1algemdcsb.xn--p1ai

Что такое касательная к окружности? Свойства касательной к окружности. Общая касательная к двум окружностям

Секущие, касательные — все это сотни раз можно было слышать на уроках геометрии. Но выпуск из школы позади, проходят года, и все эти знания забываются. Что следует вспомнить?

Сущность

Термин «касательная к окружности» знаком, наверное, всем. Но вряд ли у всех получится быстро сформулировать его определение. Между тем касательной называют такую прямую, лежащую в одной плоскости с окружностью, которая пересекает ее только в одной точке. Их может существовать огромное множество, но все они обладают одинаковыми свойствами, о которых речь пойдет ниже.

Как нетрудно догадаться, точкой касания называют то место, где окружность и прямая пересекаются. В каждом конкретном случае она одна, если же их больше, то это будет уже секущая.

История открытия и изучения

Понятие касательной появилось еще в древности. Построение этих прямых сначала к окружности, а потом к эллипсам, параболам и гиперболам с помощью линейки и циркуля проводилось еще на начальных этапах развития геометрии. Разумеется, история не сохранила имя первооткрывателя, но очевидно, что еще в то время людям были вполне известны свойства касательной к окружности.

В Новое время интерес к этому явлению разгорелся вновь — начался новый виток изучения этого понятия в сочетании с открытием новых кривых. Так, Галилей ввел понятие циклоиды, а Ферма и Декарт построили к ней касательную. Что же касается окружностей, кажется, еще для древних не осталось секретов в этой области.

Свойства

Радиус, проведенный в точку пересечения, будет перпендикулярен прямой. Это

основное, но не единственное свойство, которое имеет касательная к окружности. Еще одна важная особенность включает в себя уже две прямые. Так, через одну точку, лежащую вне окружности, можно провести две касательные, при этом их отрезки будут равны.

Есть и еще одна теорема по этой теме, однако ее редко проходят в рамках стандартного школьного курса, хотя для решения некоторых задач она крайне удобна. Звучит она следующим образом. Из одной точки, расположенной вне окружности, проведены касательная и секущая к ней. Образуются отрезки AB, AC и AD. А — пересечение прямых, B точка касания, C и D — пересечения.

В этом случае будет справедливым следующее равенство: длина касательной к окружности, возведенная в квадрат, будет равна произведению отрезков AC и AD.

Из вышесказанного есть важное следствие. Для каждой точки окружности можно построить касательную, но при этом только одну. Доказательство этого достаточно просто: теоретически опустив на нее перпендикуляр из радиуса, выясняем, что образованный треугольник существовать не может. И это значит, что касательная — единственная.

Построение

Среди прочих задач по геометрии есть особая категория, как правило, не

пользующаяся любовью учеников и студентов. Для решения заданий из этой категории нужны лишь циркуль и линейка. Это задачи на построение. Есть они и на построение касательной.

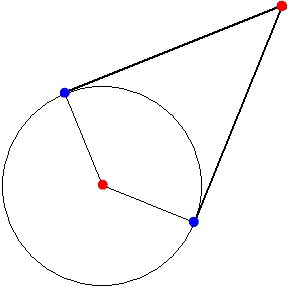
Итак, даны окружность и точка, лежащая вне ее границ. И необходимо провести через них касательную. Как же это сделать? Прежде всего, нужно провести отрезок между центром окружности О и заданной точкой. Затем с помощью циркуля следует разделить его пополам.

Чтобы это сделать, необходимо задать радиус — чуть более половины расстояния между центром изначальной окружности и данной точкой. После этого нужно построить две пересекающиеся дуги. Причем радиус у циркуля менять не надо, а центром каждой части окружности будут изначальная точка и О соответственно. Места пересечений дуг нужно соединить, что разделит отрезок пополам.

Задать на циркуле радиус, равный этому расстоянию. Далее с центром в точке пересечения построить еще одну окружность. На ней будет лежать как изначальная точка, так и О. При этом будет еще два пересечения с данной в задаче окружностью. Именно они и будут точками касания для изначально заданной точки.

Интересное

Именно построение касательных к окружности привело к рождению

дифференциального исчисления. Первый труд по этой теме был опубликован известным немецким математиком Лейбницем. Он предусматривал возможность нахождения максимумов, минимумов и касательных вне зависимости от дробных и иррациональных величин. Что ж, теперь оно используется и для многих других вычислений.

Кроме того, касательная к окружности связана с геометрическим смыслом тангенса. Именно от этого и происходит его название. В переводе с латыни tangens — «касательная». Таким образом, это понятие связано не только с геометрией и дифференциальным исчислением, но и с тригонометрией.

Две окружности

Не всегда касательная затрагивет лишь одну фигуру. Если к одной окружности можно провести огромное множество прямых, то почему же нельзя наоборот? Можно. Вот только задача в этом случае серьезно усложняется, ведь касательная к двум окружностям может проходить не через любые точки, а взаимное расположение всех этих фигур может быть очень

Типы и разновидности

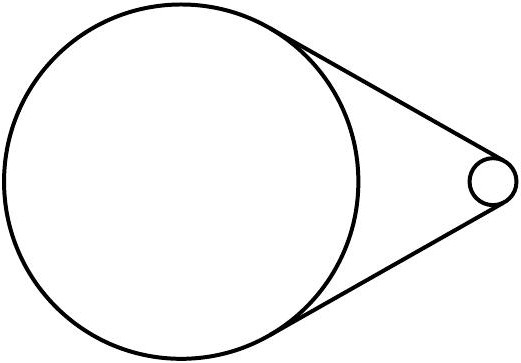
Когда речь идет о двух окружностях и одной или нескольких прямых, то даже если известно, что это касательные, не сразу становится ясно, как все эти фигуры расположены по отношению друг к другу. Исходя из этого, различают несколько разновидностей. Так, окружности могут иметь одну или две общие точки или не иметь их вовсе. В первом случае они будут пересекаться, а во втором — касаться.

И вот тут различают две разновидности. Если одна окружность как бы вложена во вторую, то касание называют внутренним, если нет — то внешним. Понять взаимное расположение фигур можно не только, исходя из чертежа, но и располагая информацией о сумме их радиусов и расстоянии между их центрами. Если две эти величины равны, то окружности касаются. Если первая больше — пересекаются, а если меньше — то не имеют общих точек.

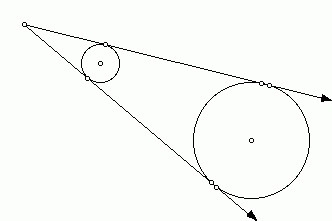
Так же и с прямыми. Для любых двух окружностей, не имеющих общих точек, можно

построить четыре касательные. Две из них будут пересекаться между фигурами, они называются внутренними. Пара других — внешние.

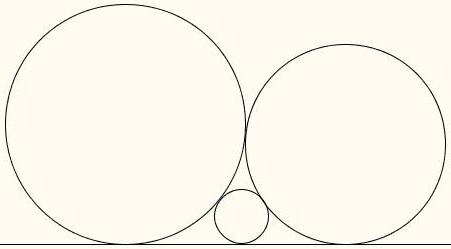
Если речь идет об окружностях, которые имеют одну общую точку, то задача серьезно упрощается. Дело в том, что при любом взаимном расположении в этом случае касательная у них будет только одна. И проходить она будет через точку их пересечения. Так что построение трудности не вызовет.

Если же фигуры имеют две точки пересечения, то для них может быть построена прямая, касательная к окружности как одной, так и второй, но только внешняя. Решение этой проблемы аналогично тому, что будет рассмотрено далее.

Решение задач

Как внутренняя, так и внешняя касательная к двум окружностям, в построении не так уж просты, хоть эта проблема и решаема. Дело в том, что для этого используется вспомогательная фигура, так что додуматься до такого способа самостоятельно

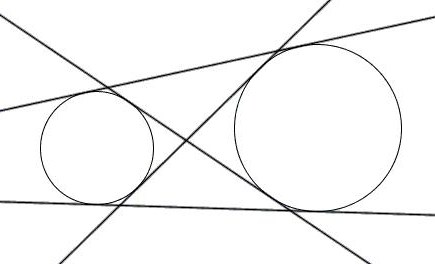
довольно проблематично. Итак, даны две окружности с разным радиусом и центрами О1 и О2. Для них нужно построить две пары касательных.

Прежде всего, около центра большей окружности нужно построить вспомогательную. При этом на циркуле должна быть установлена разница между радиусами двух изначальных фигур. Из центра меньшей окружности строятся касательные к вспомогательной. После этого из О1 и О2 проводятся перепендикуляры к этим прямым до пересечения с изначальными фигурами.

Как следует из основного свойства касательной, искомые точки на обеих окружностях найдены. Задача решена, по крайнем мере, ее первая часть.

Для того чтобы построить внутренние касательные, придется решить практически

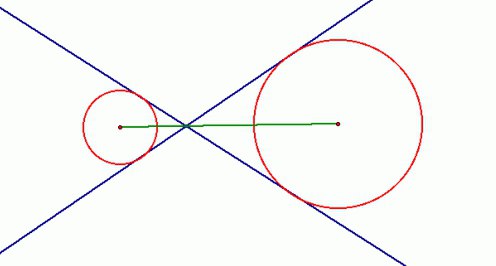
аналогичную задачу. Снова понадобится вспомогательная фигура, однако на этот раз ее радиус будет равен сумме изначальных. К ней строятся касательные из центра одной из данных окружностей. Дальнейший ход решения можно понять из предыдущего примера.

Касательная к окружности или даже двум и больше — не такая уж сложная задача. Конечно, математики давно перестали решать подобные проблемы вручную и доверяют вычисления специальным программам. Но не стоит думать, что теперь необязательно уметь делать это самостоятельно, ведь для правильного формулирования задания для компьютера нужно многое сделать и понять. К сожалению, есть опасения, что после окончательного перехода на тестовую форму контроля знаний задачи на построение будут вызывать у учеников все больше трудностей.

Что же касается нахождения общих касательных для большего количества окружностей, это не всегда возможно, даже если они лежат в одной плоскости. Но в некоторых случаях можно найти такую прямую.

Примеры из жизни

Общая касательная к двум окружностям нередко встречается и на практике, хоть это и не всегда заметно. Конвейеры, блочные системы, передаточные ремни шкивов, натяжение нити в швейной машинке, да даже просто велосипедная цепь — все это примеры из жизни. Так что не стоит думать, что геометрические задачи остаются лишь в теории: в инженерном деле, физике, строительстве и многих других областях они находят практическое применение.

Источник: fb.ru

Что такое касательная к окружности

Определение. Касательная к окружности — это прямая на плоскости, имеющая ровно одну общую точку с окружностью.

Вот парочка примеров:

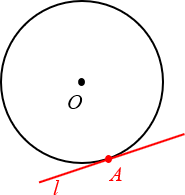
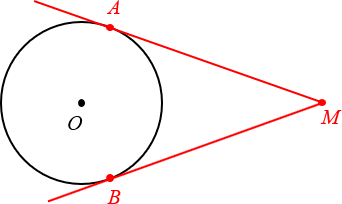
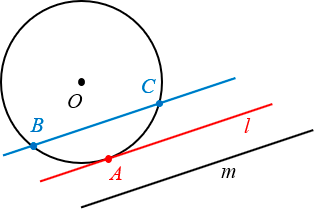
На этом можно было бы закончить, однако практика показывает, что недостаточно просто зазубрить определение — нужно научиться видеть касательные на чертежах, знать их свойства и вдобавок как следует попрактиковаться в применении этих свойств, решая реальные задачи. Всем этим всем мы сегодня и займёмся.

Основные свойства касательных

Для того, чтобы решать любые задачи, нужно знать четыре ключевых свойства. Два из них описаны в любом справочнике / учебнике, а вот последние два — про них как-то забывают, а зря.

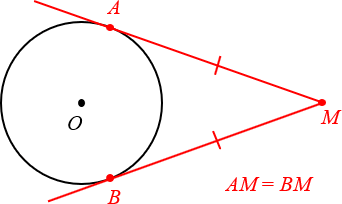
1. Отрезки касательных, проведённых из одной точки, равны

Чуть выше мы уже говорили про две касательных, проведённых из одной точки M. Так вот:

Отрезки касательных к окружности, проведённых из одной точки, равны.

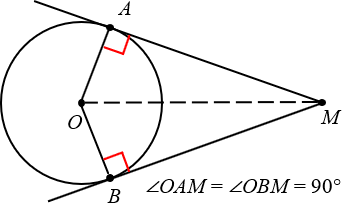
2. Касательная перпендикулярна радиусу, проведённому в точку касания

Ещё раз посмотрим на картинку, представленную выше. Проведём радиусы OAи OB, после чего обнаружим, что углы OAMи OBM — прямые.

Радиус, проведённый в точку касания, перпендикулярен касательной.

Этот факт можно использовать без доказательства в любой задаче:

Кстати, заметьте: если провести отрезок OM, то мы получим два равных треугольника: OAM и OBM.

3. Соотношение между касательной и секущей

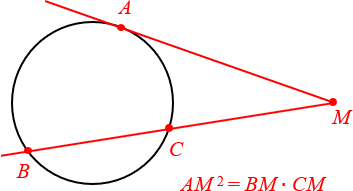
А вот это уже факт посерьёзнее, и большинство школьников его не знают. Рассмотрим касательную и секущую, которые проходят через одну и ту же общую точку M. Естественно, секущая даст нам два отрезка: внутри окружности (отрезок BC — его ещё называют хордой) и снаружи (его так и называют — внешняя часть MC).

Произведение всей секущей на её внешнюю часть равно квадрату отрезка касательной

4. Угол между касательной и хордой

Ещё более продвинутый факт, который часто используется для решения сложных задач. Очень рекомендую взять на вооружение.

Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду.

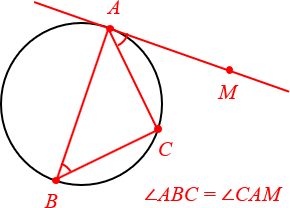
Откуда берётся точка B? В реальных задачах она обычно «всплывает» где-то в условии. Поэтому важно научиться распознавать данную конфигурацию на чертежах.

Смотрите также:

1. Вписанный угол в геометрии
2. Задачи B12, сводящиеся к линейным уравнениям
3. Геометрическая вероятность
4. Задача 18: метод симметричных корней
5. Задача B2 про комиссию в терминале
6. Значение тригонометрических функций

• ЕГЭ-2023
• Школьникам
• 1. Арифметика
• Арифметика
• Дроби
• Модуль
• Проценты
• Корни
• Степени
• Прогрессии
• Текстовые задачи
• 2. Алгебра
• Уравнения
• Системы уравнений
• Неравенства
• Системы неравенств
• Рациональные дроби
• Функции
• Многочлены
• Логарифмы
• Экспонента
• Задачи с параметром
• Вероятность
• 4. Геометрия
• Треугольники
• Многоугольники
• Окружность
• Стереометрия
• Векторы
• 3. Математический анализ
• Тригонометрия
• Предел
• Производная
• Интегралы
• Студентам
• Обо мне

Источник: www.berdov.com