Сколько осей симметрии имеет украшение изображенное

Жизнь людей наполнена симметрией. Это удобно, красиво, не нужно выдумывать новых стандартов. Но что она есть на самом деле и так ли красива в природе, как принято считать?

Симметрия

С древних времен люди стремятся упорядочить мир вокруг себя. Поэтому что-то считается красивым, а что-то не очень. С эстетической точки зрения как привлекательные рассматриваются золотое и серебряное сечения, а также, разумеется, симметрия. Этот термин имеет греческое происхождение и дословно означает «соразмерность».

Разумеется, речь идет не только о совпадении по этому признаку, но также и по некоторым другим. В общем смысле симметрия — это такое свойство объекта, когда в результате тех или иных образований результат равен исходным данным. Это встречается как в живой, так и в неживой природе, а также в предметах, сделанных человеком.

Прежде всего термин «симметрия» употребляется в геометрии, но находит применение во многих научных областях, причем его значение остается в общем и целом неизменным. Это явление достаточно часто встречается и считается интересным, поскольку различается несколько его видов, а также элементов. Использование симметрии также интересно, ведь она встречается не только в природе, но и в орнаментах на ткани, бордюрах зданий и многих других рукотворных предметах. Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.

Ось симметрии

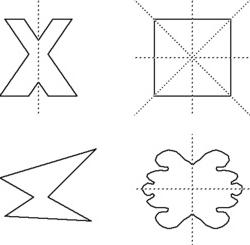
Употребление термина в других научных областях

В дальнейшем симметрия будет рассматриваться с точки зрения геометрии, однако стоит упомянуть, что данное слово используется не только здесь. Биология, вирусология, химия, физика, кристаллография — все это неполный список областей, в которых данное явление изучается с различных сторон и в разных условиях. От того, к какой науке относится этот термин, зависит, например, классификация. Так, разделение на типы серьезно варьируется, хотя некоторые основные, пожалуй, остаются неизменными везде.

Классификация

Различают несколько основных типов симметрии, из которых наиболее часто встречаются три:

• Зеркальная — наблюдается относительно одной или нескольких плоскостей. Также термин употребляется для обозначения типа симметрии, когда используется такое преобразование, как отражение.
• Лучевая, радиальная или осевая — существует несколько вариантов в различных

Кроме того, в геометрии различают также следующие типы, они встречаются значительно реже, но не менее любопытны:

• скользящая;
• вращательная;
• точечная;
• поступательная;
• винтовая;
• фрактальная;
• и т. д.

В биологии все виды называются несколько иначе, хотя по сути могут быть такими же. Подразделение на те или иные группы происходит на основании наличия или отсутствия, а также количества некоторых элементов, таких как центры, плоскости и оси симметрии. Их следует рассмотреть отдельно и более подробно.

Базовые элементы

В явлении выделяют некоторые черты, одна из которых обязательно присутствует. Так называемые базовые элементы включают в себя плоскости, центры и оси симметрии. Именно в соответствии с их наличием, отсутствием и количеством определяется тип.

Центром симметрии называют точку внутри фигуры или кристалла, в которой сходятся линии, соединяющие попарно все параллельные друг другу стороны. Разумеется, он существует не всегда. Если есть стороны, к которым нет параллельной пары, то такую точку найти невозможно, поскольку ее нет. В соответствии с определением, очевидно, что центр симметрии — это то, через что фигура может быть отражена сама на себя. Примером может служить, например, окружность и точка в ее середине. Этот элемент обычно обозначается как C.

Плоскость симметрии, разумеется, воображаема, но именно она делит фигуру на две равные друг другу части. Она может проходить через одну или несколько сторон, быть параллельной ей, а может делить их. Для одной и той же фигуры может существовать сразу несколько плоскостей. Эти элементы обычно обозначаются как P.

Но, пожалуй, наиболее часто встречается то, что называют «оси симметрии». Это нередкое явление можно увидеть как в геометрии, так и в природе. И оно достойно отдельного рассмотрения.

Оси

Часто элементом, относительно которого фигуру можно назвать симметричной,

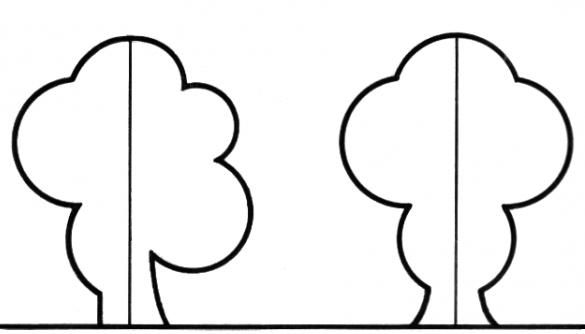
выступает прямая или отрезок. В любом случае речь идет не о точке и не о плоскости. Тогда рассматриваются оси симметрии фигур. Их может быть очень много, и расположены они могут быть как угодно: делить стороны или быть параллельными им, а также пересекать углы или не делать этого. Оси симметрии обычно обозначаются как L.

Примерами могут служить равнобедренные и равносторонние треугольники. В первом случае будет вертикальная ось симметрии, по обе стороны от которой равные грани, а во втором линии будут пересекать каждый угол и совпадать со всеми биссектрисами, медианами и высотами. Обычные же треугольники ею не обладают.

Кстати, совокупность всех вышеназванных элементов в кристаллографии и стереометрии называется степенью симметрии. Этот показатель зависит от количества осей, плоскостей и центров.

Примеры в геометрии

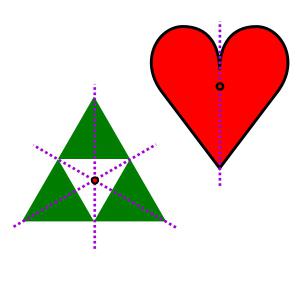
Условно можно разделить все множество объектов изучения математиков на фигуры, имеющие ось симметрии, и такие, у которых ее нет. В первую категорию автоматически попадают все правильные многоугольники, окружности, овалы, а также некоторые частные случаи, остальные же попадают во вторую группу.

Как и в случае, когда говорилось про ось симметрии треугольника, данный элемент для четырехугольника существует не всегда. Для квадрата, прямоугольника, ромба или параллелограмма он есть, а для неправильной фигуры, соответственно, нет. Для окружности оси симметрии — это множество прямых, которые проходят через ее центр.

Кроме того, интересно рассмотреть и объемные фигуры с этой точки зрения. Хотя бы одной осью симметрии помимо всех правильных многоугольников и шара будут обладать некоторые конусы, а также пирамиды, параллелограммы и некоторые другие. Каждый случай необходимо рассматривать отдельно.

Примеры в природе

Зеркальная симметрия в жизни называется билатеральной, она встречается наиболее
часто. Любой человек и очень многие животные тому пример. Осевая же называется радиальной и встречается гораздо реже, как правило, в растительном мире. И все-таки они есть. Например, стоит подумать, сколько осей симметрии имеет звезда, и имеет ли она их вообще? Разумеется, речь идет о морских обитателях, а не о предмете изучения астрономов.

И правильным ответом будет такой: это зависит от количества лучей звезды, например пять, если она пятиконечная.

Кроме того, радиальная симметрия наблюдается у многих цветков: ромашки, васильки, подсолнухи и т. д. Примеров огромное количество, они буквально везде вокруг.

Аритмия

Этот термин, прежде всего, напоминает большинству о медицине и кардиологии, однако он изначально имеет несколько другое значение. В данном случае синонимом будет «асимметрия», то есть отсутствие или нарушение регулярности в том или ином виде. Ее можно встретить как случайность, а иногда она может стать прекрасным приемом, например, в одежде или архитектуре. Ведь симметричных зданий очень много, но знаменитая Пизанская башня чуть наклонена, и хоть она не одна такая, но это самый известный пример. Известно, что так получилось случайно, но в этом есть своя прелесть.

Кроме того, очевидно, что лица и тела людей и животных тоже не полностью симметричны. Проводились даже исследования, согласно результатам которых «правильные» лица расценивались как неживые или просто непривлекательные. Все-таки восприятие симметрии и это явление само по себе удивительны и пока не до конца изучены, а потому крайне интересны.

Источник: fb.ru

Урок 32. Осевая и центральная симметрии

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок. Центр симметрии — это точка, в которой пересекаются все оси симметрии. Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Симметрия геометрических фигур и тел

Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.

А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен.

Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.

Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.

У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.

Видео

Центральная симметрия

Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.

Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.

Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

Рис. 2 Графическое представление центральной симметрии

Фигуры, имеющие несколько осей симметрии

Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.

Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.

То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.

Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.

Рис. 5 Оси симметрии ромба

Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.

Рис. 6 Оси симметрии равностороннего треугольника

В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.

Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.

Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.

Источник: 2cheloveka.ru

wiki.eduVdom.com

Записаться
на занятия (831) 247 47 55
eduVdom.com

Геометрия:

Контакты

eduVdom.com
+7 910 874 73 73
+7 904 064 04 04
Больше контактов.
Оставить отзыв.
subjects:geometry:центральная_и_осевая_симметрии
Четырехугольники
Центральная и осевая симметрии

Центральная и осевая симметрии

Центральная симметрия

Две точки А и А1 называются симметричными относительно точки О, если О — середина отрезка АА1 (рис.1). Точка О считается симметричной самой себе.

Пример центральной симметрии

Точки А и А1 – симметричные относительно точки О

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.

Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм (рис.2).

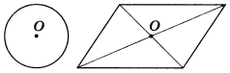
Фигуры, обладающие центральной симметрией

Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма — точка пересечения его диагоналей. Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии (точка О на рис.2), у прямой их бесконечно много — любая точка прямой является ее центром симметрии.

Осевая симметрия

Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему (рис.3). Каждая точка прямой а считается симметричной самой себе.

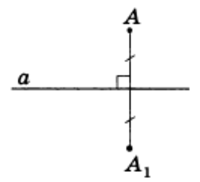
Точки А и А1 — симметричные относительно прямой а

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.

Примеры таких фигур и их оси симметрии изображены на рисунке 4.

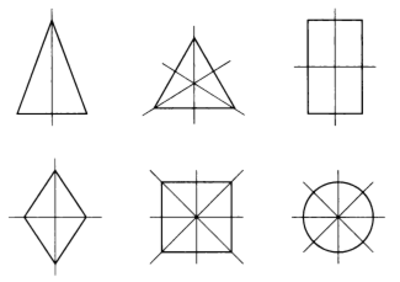
Заметим, что у окружности любая прямая, проходящая через ее центр, является осью симметрии.

Сравнение симметрий

Центральная и осевая симметрии

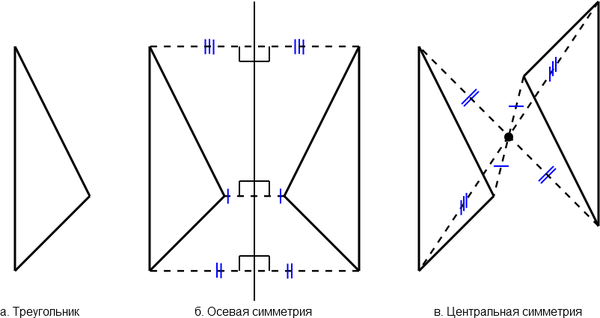
Построение треугольника (а) симметрично относительно оси (б) и точки (в)

Пример

Сколько всего осей симметрии имеет фигура, изображённая на рисунке?

Дополнительно

Геометрия ( Справочник )

Рекомендуем для обучения:

YouTube

← Трапеция	Пропорциональные отрезки →
Оси симметрии на YouTube
Подобие произвольных фигур

subjects/geometry/центральная_и_осевая_симметрии.txt · Последние изменения: 2022/04/01 20:09 — ¶

Инструменты страницы

• Показать исходный текст
• История страницы
• Ссылки сюда
• Свернуть / развернуть всё
• Наверх

Записаться на занятия

Записаться на занятия к репетитору

• +7 (910) 874 73 73
• +7 (905) 194 91 19
• +7 (831) 247 47 55

Источник: www.wiki.eduvdom.com